วีดีโอ

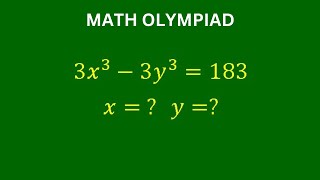
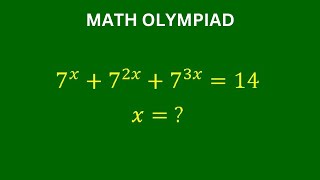
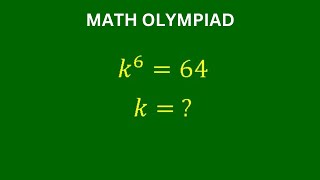
A Very Nice Math Olympiad Problem: [(x + 2)(x + 3)(x + 4)(x + 5)]/[(x - 2)(x - 3)(x - 4)(x - 5)] = 1; x =? [(x + 2)(x + 5)][(x + 3)(x + 4)] = (x² + 7x + 10)(x² + 7x + 12) = (x² + 10 + 7x)(x² + 12 + 7x) = (x² + 10)(x² + 12) + 14x(x² + 11) + (7x)² [(x - 2)(x - 5)][(x - 3)(x - 4)] = (x² - 7x + 10)(x² - 7x + 12) = (x² + 10 - 7x)(x² + 12 - 7x) = (x² + 10)(x² + 12) - 14x(x² + 11) + (7x)² (x + 2)(x + 3)(x + 4)(x + 5) = (x - 2)(x - 3)(x - 4)(x - 5) (x² + 10)(x² + 12) + 14x(x² + 11) + (7x)² = (x² + 10)(x² + 12) - 14x(x² + 11) + (7x)² 28x(x² + 11) = 0, x(x² + 11) = 0; x = 0 or x² + 11 = 0, x² = - 11; x = ± i√11 Answer check: [(x + 2)(x + 3)(x + 4)(x + 5)]/[(x - 2)(x - 3)(x - 4)(x - 5)] = [(x² + 7x + 10)(x² + 7x + 12)]/[(x² + 7x + 10)(x² + 7x + 12)] = 1 x = 0: [(2)(3)(4)(5)]/[(- 2)(- 3)(- 4)(- 5)] = 1; Confirmed x = ± i√11: x² = - 11 x² + 7x + 10 = - 11 ± 7i√11 + 10 = - 1 ± 7i√11, x² + 7x + 12 = 1 ± 7i√11 (x² + 7x + 10)(x² + 7x + 12) = (- 1 ± 7i√11)(1 ± 7i√11) = - 1 - 539 = - 540 x² - 7x + 10 = - 1 -/+ 7i√11, x² - 7x + 12 = 1 -/+ 7i√11 (x² - 7x + 10)(x² - 7x + 12) = (- 1 -/+ 7i√11)(1 -/+ 7i√11) = - 1 - 539 = - 540 [(x² + 7x + 10)(x² + 7x + 12)]/[(x² + 7x + 10)(x² + 7x + 12)] = 1; Confirmed Final answer: x = 0; x = i√11 or x = - i√11

as per the question...it is very visible...base ...k-1=2...so k=3❤

[(x + 2).(x + 3).(x + 4).(x + 5)] / [(x - 2).(x - 3).(x - 4).(x - 5)] = 1 (x + 2).(x + 3).(x + 4).(x + 5) = (x - 2).(x - 3).(x - 4).(x - 5) (x² + 3x + 2x + 6).(x² + 5x + 4x + 20) = (x² - 3x - 2x + 6).(x² - 5x - 4x + 20) (x² + 5x + 6).(x² + 9x + 20) = (x² - 5x + 6).(x² - 9x + 20) x⁴ + 9x³ + 20x² + 5x³ + 45x² + 100x + 6x² + 54x + 120 = x⁴ - 9x³ + 20x² - 5x³ + 45x² - 100x + 6x² - 54x + 120 28x³ + 308x = 0 28x.(x² + 11) = 0 x.(x² + 11) = 0 First case: x = 0 Second case: x² + 11 = 0 x² = - 11 x² = 11i² x = ± i√11

Substitute x=2 by trial and error method( a+b)^2+(a-b)^2 =2a^2+2b^2 which is equal to 2×4^2+2(√15)^2= 32+30=62

The equation satisfy at x = 0

Using assumption method x = 2 (4 + √15)^x + (4 -√15)^x =( 4+ √15)^2 + (4 - √15)^2 {4^2 + 2.4.√15 + (√15)^2} + {4^2 - 2.4.√15 + (√15)^2} =(4^2 + 2.4.√15 +(√15)^2) +(4^2 - 2.4.√15 + (√15)^2) =4^2 + 8√15 + 15 +4^2 - 8√15 + 15 2.16 + 15 + 15 (canceling+8√15 and -8√15) = 32 + 30 =62 =R H S Hence assumption is correct Therefore x = 2

Có nhiều cách giải bài toán này, cảm ơn bạn chia sẻ kinh nghiệm cho các bạn trẻ, tôi đã 60 tuổi nhưng vẫn nhớ kiến thức này từ Việt Nam 🤝

x * (x + 2) * (x + 4) * (x + 6) = 9 (x^2 + 2x) * (x^2 + 10x + 24) = 9 x^4 + 10x^3 + 24x^2 + 2x^3 + 20x^2 +48x = 9 x^4 + 12x^3 + 44x^2 + 48x - 9 = 0 Now, let's factor. x^4 is multiplies by 1, and the polynomial ends in negative 9. So, let's try x = + 3 and x = -3 x = +3 3 * 5 * 7 * 9 = 9 FAIL x = -3 -3 * -1 * 1 * 3 = 9 PASS x = -3 ... (x + 3) Now, divide the polynomial by (x + 3) (x + 3) * (x^3 + 9x^2 + 17x - 3) = 0 Now, try to factor... We still have a -3, so this new polynomial might still be divisible by (x + 3), let's give it a go... And it does factor... (x + 3)^2 * (x^2 + 6x - 1) That last polynomial doesn't look like it factors cleanly, but no matter... Now set both equal to zero and let's find our x. (x + 3) = 0 x = -3 x^2 + 6x - 1 = 0 Move over and complete the square... x^2 + 6x + 9 = 1 + 9 (x + 3)^2 = 10 x + 3 = [+/-]sqrt(10) x = -3 + [+/-]sqrt(10) x= -3 ; -3 + sqrt(10) ; -3 - sqrt(10)

❤ Let y = x/(x-1) then x+ y = xy equation is x^2+y^2 = 8 or (x+y)^2 - 2xy = 8 (xy)^2 - 2xy - 8 = 0 xy = 4 , -2 putting in x+y = xy Case 1 x+ 4/x = 4 x^2 - 4x +4 = 0 x = 2 Case 2 x - 2/x = -2 x^2+2x = 2 (x+1)^2 = 3 x = -1+√3 , x = - 1-√3 indirectly we have to find point of intersection of circle and rectangular hyperbola.👍

X=+-√11i X=+-✓11√(-1) ,√(-1)=i X=+-√11i NO. +-√-11i

when we check the solutions, we have sqrt(521i)+sqrt(-512i)=32i or -32i √x+√(-x)=√512i+√(-512i) =√512∙√i+√512∙√(-i) =√512∙(√i+√(-i)) i=0+i∙1=cos(π/2)+i∙sin(π/2)=e^(π/2 i)=e^(2nπ+π/2)i，n∈Z √i=(i)^(1/2)=e^(nπ+π/4)i=cos(nπ+π/4)+i∙sin(nπ+π/4) √(-i)=(i)^(3/2)=e^(3nπ+3π/4)i=cos(3nπ+3π/4)+i∙sin(3nπ+3π/4) take n=0 √i=cos(π/4)+i∙sin(π/4)=1/√2+1/√2 i √(-i)=cos(3π/4)+i∙sin(3π/4)=-1/√2+1/√2 i √i+√(-i)=1/√2+1/√2 i+(-1/√2+1/√2 i)=2/√2 i=√2 i √x+√(-x)=√512∙√2 i=32i take n=1 √x+√(-x)=√512∙(-√2 i)=-32i Why?? Do have any wrong??

Should have gone straight to using the log of base 2/5 to minimize the number of steps in solving the exponential equation. Applying the appropriate log base to the exponential equation allows using whatever is in the exponent on one side of the equation to be the only thing on that side of the equation.

(4x+4x ➖}+{25x+25x ➖}={8x^2+50x2}=58x^4 8^50x^4 8^25^25^x^2 8^5^5^5^5^5^5^5^5^5^5x^4 2^3^2^3^2^3^2^3^2^3^2^3^2^3^2^3^2^3^2^3^2^3x^2^2 1^1^1^1^1^1^1^1^1^1^1^1^1^1^1^1^1^1^1^1^1^1^3x^1^2 1^3x^1^2 3x^2(x ➖ 3x+2). 10^{x+x ➖ }+{1+1 ➖ }=10^{x^2+2}=2)10^2x^2 20x^2 10^10x^2 5^5^5^5x^2 2^3^2^3^2^3^2^3x^2 1^1^1^1^1^1^1^3x^2 3x^2 (x ➖ 3x+2).

(16)+(16) (2^3)+(2^3) (2^1)+(2^1) (1)+(2) (a ➖ 2a+1)

{61+61}=121 10^10^21 1^10^3^7 2^5^2^53^7^1 1^1^2^1^31^1 2^3:(y ➖ 3x+2).

I have read most of the comments and concluded that that the method used in this problem is very good.

Can’t the answer be simplified?

61=(-1)*(-61) Где этот вариант?

What if x=1 and y=-1 in equality (x-y) < x^2+xy+y^2 ?? Or x=y=0? x=2 ,y=-2?

Check 61+y^3 for y=1, 2, 3, 4, bingo! 5^3-4^3 = 61, hence (x,y)=(5,4) or (-4,-5). This is not an IMO-class problem.

Step one and step two can be done in one go you don't have to do every tiny operation

(7^x)+[7^(2x)]+7^(3x)=14 (7^x)+(7^x)²+(7^x)³=2+4+8 =2+2²+2³ As the structure of bot side is similar 7^x=2 --> x=⁷log(2) where the logarithm is 7-based. For other possibile roots, knowing that [(7^x)-2] is a factor, we can factor the equation as (7^x)³+(7^x)²+(7^x)-14=0 [(7^x)-2][(7^x)²+3(7^x)+7]=0 (7x^x)²+3(7^x)+7=0 is a quadratic equation which is positive definite. The roots are imaginary: 7^x=½[-3±isqrt(19)] Have to take logarithm to find x, which can't be done.

How do we know a quartic equation without a cubic can be factorised as (x²+x+p)(x²-x+q) and does it still hold true even when there is a cubic? Also is there any reasoning why the coefficient of x equals 1 anyway? 😄

Notice that in the video, I only considered the positive factors of 61. You can try the negative factors of 61 and show us what you've got. ❤

First❤❤❤❤

Easier with the polar writing. Set i = (1,pi/2 + 2k.pi) with k = 0 or 1. Then for k = 0 ==> sqrt(i) = (1,pi/4) = (sqrt(2)/2).(1 + i) for k = 1 ==> sqrt(i) = (1,pi/4 + pi) = (-sqrt(2)/2).(1 + i)

(√a+√-a)^2=32^2;=>a+2(√a√-a)-a= 1024;=>2(√a√-a)= 1024;=> √(-a^2)= 512;=> a=±512i

Hoc est x= log 2/ log7, Eheu! Responsi. 😂😅😊😢🎉😂😅😊😮😢

At about 4:30 the lecturer is cheating: The tentative factorization over the integers must take the form (x^2+rx+p)(x^2-rx+q) There is no stated prior reason why r should equal 1 (except by already knowing the result)! With r unknown a completely different solution strategy must be adopted, based on all possible factorizations of the constant term.

Introduce y=√(x+5), and rewrite equation as x^2 - y = 5 y^2 - x = 5 Subtract to find x^2 -y^2+x-y=(x-y)(x+y+1)=0. Case y=x => (after squaring) (x-1/2)^2 = 5+1/4 = 21/4 x=(1+√21)/2 is a valid solution, x=(1-√21)/2 is not a valid expression for y as a square root. Case y=-(x+1) => (after squaring) (x+1/2)^2 = 5-1+1/4 = 17/4 x=-(1+√17)/2 is a valid solution. x=(-1+√17)/2 does not lead to a valid expression for y as a square root.

Let a=±bi where b is real. Then √2√b/2=16. Thus, √b=16√2, b=2*16^2=512, and a=±512i

为什么能展开成这两个二次方程的乘积 我随便写了个方程，就无法这样做 x^4 -22x^2+3x+8=0

(x-3)^4=16 x=5 5 - 3 = 2 2^4 =16

What is the value of “log of a complex number” ? Are there any definition of it value?

much simpler in polar coordinates. x⁶≉2⁶ exp(i2nπ) x=2exp(iπ2n/6) =2exp(iθ) θ=0, π/3, 2π/3, π, 4π/3, 5π/3. note exp(iθ)= cosθ +isinθ so solutions are x=±2, 2(cos60±isin60), 2( cos120±isin120) x=±2, 1±i√3 , −1±i√3 it helps to draw the solutions on the Argand diagram. The solutions are six equally spaced points on a circle radius 2

I tried x^4-14x+5x+30=0, using your method, but the system of equations was q-p=5, q+p=-13 and qp=30. Two of the solutions involved quadratics with “c” that contained a square root for a coefficient.

(X^2 - Y^2) = (X+Y)(X-Y)=24; 24=12x2, the sum of X+Y and X-Y is 2X = 14 and X= 7 and Y= 5. This is the answer in natural numbers

It’s tricky, but not as hard as partial fractions.

(x^2)^2 ➖(5)^2={x^4 ➖ 25}=21 3^7 3^7^1 3^1^1 3^1 (x ➖ 3x+1). {x+x ➖ }+{5+5 ➖ }={x^2+10}=10x^2 5^5x^2 2^3^2^3x^2 1^1^1^3x^2 3x^2 (x ➖ 3x+2).

(x⁸ - x²)/(x⁴ - x²) = 9 , (x⁴ - x²) ≠ 0 -> x ≠ 0, ±1 (x⁶ - 1)/(x² - 1) = 9 x⁴ + x² + 1 = 9 x⁴ + x² - 8 = 0 x² = (-1 ± √33)/2 = 2*(-1 ± √33)/4 x = ±√2*√(√33-1)/2, ±i*√2*√(√33+1)/2

La equis subuno en positiva mayor que cero la que es negativa es la equis subidos

One obvious solution is x = ln(2)/ln(7).

let u=7^x , u^3+u^2+u-14=0 , (u-2)(u^2+3u+7)=0 , u=2 , 7^x=2 , x=log2/log7 , 1 -2 test , 7^x+7^2x+7^3x=2+4+8 , --> 14 , OK , 3 -6 /u^2+3u+7=0 , u=(-3+/-V(9-28))/2 , u=(-3+/-i*V(19))/2/ , 7 -14

{14+28x^2+21x^3}=63x^4 14 2^14x^2+3^7x^3 2^7x^2+2^3^7x^3+ 1^1+1^1x^1+ 1^3^4x^1 3^2^2 x^1 3^1^2x^1 3^2x (x ➖ 3x+2).

7ˣ = 2 (2 + 4 + 8 = 14) x = log₇2

X=log2/ log7 (log 2 with base 7)

For logs, you would save steps if you use the log base that cancels out leaving with whatever is in the exponent. In this case, the extra steps would not have been necessary had you simply introduced the log to base 7 on both sides of the equation.

7^x+7^2x+7^3x=14 (7^x)³+(7^x)²+7^x-14=0 Let y=7^x y³+y²+y-14=0 y³-8+y²-4+y-2=0 (y-2)(y²+2y+4)+(y-2)(y+2)+1(y-2)=0 (y-2)(y²+3y+7)=0 y²+3y+7=0 ∆=b²-4ac ∆=3²-4•1•7 ∆=-19<0 reject y-2=0 y=2 7^x=2 x=log_7(2) ❤

I mean what is wrong if we took matual 7 to the power x and its 1+1²+1³=14 It's not working but i want to know why can you explain plz

Thanks for the video. You are touching on a very tricky topic. The definition of the log of a complex number leads to some contradictions which need exclusion and specific treatment. To say it differently I would not touch this animal :-). By the way I think that dividing the polynomial by t-2 (knowing that 2 is "evident" solution) and solving the quadratic equation is a shorter path. Good job anyway.