วีดีโอ

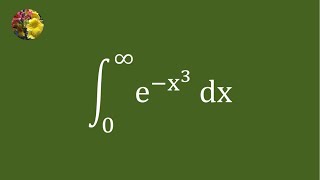
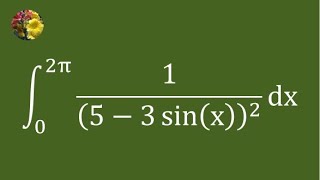
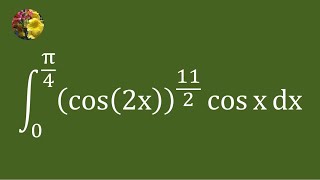
This is a classic!! The Gudermannian Function, which relates the area of the circus sector to the area of the hyperbolic sector! gf(x) = \int_{0}^{x} 1/(cosh(t) dt I was just looking at this this morning.

1/cosh(x)=cosh(x)/cosh^2(x) cosh^2(x) - sinh^2(x) = 1 cosh^2(x) = 1 + sinh^2(x) cosh(x) is even so we have 2\int_{0}^{\infty}\frac{cosh(x)}{1+sinh^2(x)}dx 2arctan(sinh(x))|_{0}^{\infty} = \pi

Nice

Wow, this is crazy.

Break in two integrals , using IBP by taking unity as second function integral of e^ { (ln x)^2 } = e^ { ( ln x)^2 } x - integral of e^ { (ln x)^2 } (2 ln x)(1/x)x after cancellation of integral I = x e^ { ( ln x)^2 }

Wow such a cool integral!

Another potential solution: Consider I(t)=integral 0 to 2π of 1/(t-3sinx). Calculate I(t) using standard techniques or Weierstrass substitution. Integrate the result of I(t) twice to get I''(t). Replace t by 5 in the result of I"(t) for the final answer. Raghvendra Singh proposed about these exact steps to solve the integral with cos(x) in the integrand instead of sin(x). This approach is worth perhaps monkeying here.

A very short way : set y= √i *x and consider e^(i*x^2) : then our integral becomes √i *∫e^(-y^2) dy (0 to ∞ ) = √π /2 *√i , and taking the real part :√π /√8 .

Excellent

Proposition for video Let f(x) = \sum_{k=0}^{\infty}a_{k}T_{k}(x) where a_{k} = \frac{(2-\delta_{k0})}{\pi}\int_{-1}^{1}\frac{f(x)T_{k}(x)}{\sqrt{1-x^2}}dx We can cubstitute x = \cos{t} to get a_{k} = \frac{(2-\delta_{k0})}{\pi}\int_{0}^{\pi}f(\cos{t})cos(kt)dt This delta is the Kronecker symbol How to calculate this integral I know that there exists formula without integral

Another solution I solved. e^(lnx)²=x^lnx...(1) Now let's replace it with x^lnx=t. Since lnt=(lnx)², if you differentiate it, dt/t=2lnxdx/x...(2) the whole formula §t(1+2lnx)dx=§tdx+§xdt(by(2)))=xt=x^(lnx)²+C=xe^(lnx)²+C■

Hey there 🤗 thanks for the video 😊. You got a new subscriber ❤.

A self made problem with solution Problem - evaluate integral of { √( 3 cos h 2x + 4 - 3 sin h 2x) } { e^( - 10x) cos h x } in [0, infinity] solution - I = integral of √{ 4+3e^( - 2x) } { e^( - 3x) } { e^( - 7x) } { e^(x)+e^( - x) }/2 I = (1/2) integral of √{4e^( - 6x)+3e^( -8x) } { e^( - 6x)+e^( - 8x) } now put expression under square root = t^2 I = (1/24) integral of t^2 in [0, √7] I = (7√7) / 72

Not that difficult for those watching this channel for a while, and very inspirational for debutants.

Use substitution cos(x) = (1 - sin(x))t cos^2(x) = (1 - sin(x))^2t^2 (1 - sin^2(x)) = (1 - sin(x))^2t^2 (1 - sin(x))(1 + sin(x)) = (1 - sin(x))^2t^2 1 + sin(x) = (1 - sin(x))t^2 1 + sin(x) = t^2 - sin(x)t^2 sin(x)+sin(x)t^2 = t^2 - 1 sin(x)(t^2 + 1) = t^2 - 1 sin(x) = (t^2 - 1)/(t^2 + 1) cos(x) = (1 - (t^2 - 1)/(t^2 + 1))t cos(x) = 2t/(t^2 + 1) cos(x)dx = (2t(t^2+1)-2t(t^2-1))/(t^2+1)^2dt cos(x)dx = 4t/(t^2+1)^2dt 2t/(t^2 + 1)dx = 4t/(t^2+1)^2dt dx = 2/(t^2+1)dt sqrt(5)-cos(x) = sqrt(5) - 2t/(t^2+1) sqrt(5)-cos(x) = (sqrt(5)t^2 - 2t + sqrt(5))/(t^2+1) But to use substitution we must divide interval of integration into two pieces \int_{1}^{\infty}\frac{(t^2+1)^3}{(\sqrt{5}t^2 - 2t + \sqrt{5})^3}\cdot\frac{2}{(t^2+1)}dt +\int_{-\infty}^{-1}\frac{(t^2+1)^3}{(\sqrt{5}t^2 - 2t + \sqrt{5})^3}\cdot\frac{2}{(t^2+1)}dt 2(\int_{-\infty}^{-1}{\frac{(t^2+1)^2}{(\sqrt{5}t^2 - 2t + \sqrt{5})^3}}dt + \int_{1}^{\infty}{\frac{(t^2+1)^2}{(\sqrt{5}t^2 - 2t + \sqrt{5})^3}}dt) then use substitution t - 1/sqrt{5} = \frac{2}{\sqrt{5}}u

I was very impressed by this solution the moment I read it as a comment in another video with the same integral. Thanks for this video post.

Have an idea for problem no method thinking about converting the cos(x)=cos(2*x/2)=cos^2(x/2)-sin^2(x/2) from there ((5)^1/2-(cos^2(x/2)-sin^2(x/2))) ((5)^1/2-(1-sin^2(x/2)-sin^2(x/2)) ((5)^1/2-(1-2sin^2(x/2))) sec^6(x/2)/(sec^6(x/2)((5)^1/2-1+2sin^2(x/2))^3

third method let x = 1/t I = integral of arc cot t in [0,1] using IBP by taking unity as second function I = π/4+ integral of t/(t^2+1) I = π/4+(1/2) ln 2

I would calculate this integral the same way as you

Please how do I make a video like this... I'll really be grateful if someone responds

Wow... Nice

putting x = tan t I = integral of t ( cosec t)^2 in [π/4,π/2] using IBP by taking t as first function I = π/4+(1/2) ln 2

Beautiful solution from Raghvendra Singh

Excellent

Another marvel with the Weierstrass substitution!

Another approach Start with the integral I(a) = 0 to π intg (1/(a-cosx)) . Apply king's rule now I(a) = (1/(a+cosx)). Add the 2 versions of it 2I(a) = 2a/a²-cos²x . Write cosx as 1/secx . Now I(a) = asec²x/a²sec²x-1 . Put tanx = t . Sec²xdx becomes dt . I(a) = adt/a²(1+t²)-1 = adt/a²t² + a²-1 . Apply the formula of integral of dx/x²+a² . Back substitute the limits t = tanx and the limits of integral . Now we have I(a) in terms of a . Differentiate it twice wrt a to get (a-cosx)³ in the denominator. Finally put a = √5 and we're done ✅

Excellent

not very sick

slightly sick

z^3 = i z^3+ i^3 = 0 because i^2 = - 1 (z+i) (z^2 - iz - 1) = 0 z = - i , (i+√3)/2 , ( i - √3)/2

Another method sin^2(x)/(sin^4(x)-1) sin^4(x)/(sin^2(x)(sin^4(x)-1)) (sin^4(x)-1+1)/(sin^2(x)(sin^4(x)-1)) (sin^4(x)-1)/(sin^2(x)(sin^4(x)-1)) +1/(sin^2(x)(sin^4(x)-1)) 1/sin^2(x)+1/(sin^2(x)(sin^2(x)+1)(sin^2-1)) csc^2(x)-1/(sin^2(x)(sin^2(x)+1)(1-sin^2(x)) csc^2(x)-1/(sin^2(x)(sin^2(x)+1)cos^2(x)) csc^2(x)-sec^2(x)/(sin^2(x)(sin^2(x)+1)) csc^2(x)-sec^4(x)sec^2(x)/(tan^2(x)(tan^2(x)+sec^2(x)) csc^2(x)-(tan^2(x)+1)^2sec^2(x)/(tan^2(x)(2tan^2(x)+1)) Let u=tan(x) du=sec^2(x) dx csc^2(x)-(u^2+1)^2/(u^2(2u^2+1)) csc^2(x)-(u^4+2u^2+1)/(u^2(2u^2+1)) csc^2(x)-u^4/(u^2(2u^2+1)+(2u^2+1)/(u^2(2u^2+1)) csc^2(x)-u^2/(2u^2+1)+1/u^2 csc^2(x)-1/2 integral 2u^2+1-1/(2u^2+1)+1/u^2 csc^2(x)-1/2integral 1-1/(2u^2+1)+1/u^2

Another method Sin^2(x)/(sin^4(x)-1) Sin^2(x)/((sin^2(x)+1)(sin^2(x)-1) Sin^2(x)/((sin^2(x)+1)(-(1-sin^2(x)) Put negative 1 infornt intgral sin^2(x)/((sin^2(x)+1)(1-sin^2(x)) Sin^2(x)/((sin^2(x)+1)(cos^2(x)) Sin^2(x)sec^2(x)/(sin^2(x)+1) tan^2(x)/(sin^2(x)+1) tan^2(x) sec^2(x)/((sin^2(x)+1)sec^2(x)) tan^2(x) sec^2(x)/(tan^2(x)+sec^2(x)) tan^2(x)sec^2(x)/(2tan^2(x)+1) Let u=tan(x) du=sec^2(x) dx u^2/(2u^2+1) -1/2 intgral 2u^2/(2u^2+1) -1/2 integral (2u^2+1-1)/(2u^2+1) -1/2 integral 1-1/(2u^2+1)

Perfect. Now try substitute sin^4 on top and sin^6 on bottom!

It is possible to calculate indefinite integral by parts First integration by parts u = ln(t) dv = t^3/(1+t^4)^3 dt Second integration by parts u = 1/t^4 , dv = t^3/(1+t^4)^2 dt You have integral of 1/(t^5(1+t^4)) then you can change of variable u = 1 + 1/t^4 Once you have antiderivative you can take the limits

I ran into something new in connection with physics integral, called Sommerfeld expansion.Also here is an integral that was on an elite Russian Physics graduate entrance exam: Indefinite integral: Sin^2(x)/(Sin^4(x)-1) dx.

Fantastic

slightly sick but such a very cool trick

Ottimo Boys. Hai applicato Feyman con il trucco algebrico di scrivere 2 come 1+1. Senza infatti questo trucco l'integrale non sarebbe calcolabile con la tecnica di Feyman perche' mi pare di ricordare che per a = 1, l'integrale non converge o e' pari a zero.

P. How do you make this animation? What software you use

why not substitute 1/(x^2+1)=t?

I love how the best solution to an integral can range from a complex algebraic transformation to a very simple yet very hidden technique, and the person solving the integral is the one who must find it.

Excellent

Excellent

Can I have problem for you ? Expand function f(t) = 1/sqrt(1-2xt+t^2) to power series I used binomial expansion twice and I had got n + k as power of t but I need n as power of t because it is generating function of sequence of polynomials

An elegant way is to use residue-theory for e^(a*i*x^2). The residues in the upper half-plane are given by e^(i a x^2)/(4*x^3) for x=√i and x = √(- i). You then calculate 2 π i * sum of residues and take real and imaginary parts. You end up with e^(-a)π/√2 .

Fantastic ❤️❤️❤️❤️

Or, you can just take I(a)'s derivative twice, using Fresnel integral, we can easily prove I''(a)=I(a), which means I(a)=A*e^a+B*e^(-a), and using I(0)=pi/√2 and I'(0)=-pi/√2, we can get that A=0, B=pi/√2, so I(a)=(pi/√2)*e^(-a).

Nice.🎉

Algebraic manipulations ? 1 = 1 + x^2 - x^2

Let x^2 = 1/t I = (1/2) integral of t/(t+1) in [ 0,1] I = (1/2) (1 - ln 2)