วีดีโอ

1) For newcomers, the m in 7m is confusing, since it could be a dimension m = meters or a variable. (Those who have studied other problems from Math and Engineering will know that it is meters.) 2) Starting at 4:00, 7203 could simply be factored into 3 times 2401. Since 2401 = 49², we can take 49 outside the radical, so √(7203) = 49√3 (4:45). 3) As matthieudutriaux pointed out, the solution finds that B (1:30 in the video) is the midpoint of QR and A and R are the same point. Therefore, the drawing is not correct, because it shows A as a point on PR between P and R. The solution method, however, is still valid. It looks like this solution method would still give the correct answer if B were anywhere on the semicircle. Assuming that angles can only have positive measures, when B is outside the equilateral triangle to its right, a can have a positive value but must be added to 60° instead of subtracted to produce an angle <ARB greater than 60°. However, subtracting a negative angle produces the same result.

My trigonometry version without any construction lines to share with. <QBP+<PBR+<QBR=360, <PBR=90, hence <QBP=270-<QBR cos(<QBP)=cos(270-<QBR)=-sin(<QBR) cos(<QBP)^2+cos(<QBR)^2=(-sin(<QBR)^2+cos(<QBR)^2=1 ……..(1) Let z=QP=QR=PR=2*r, then z^2=x^2+y^2 Applying cosine law to triangle QBP and QBR (7^2+y^2-z^2)/(2*7*y)=cos(<QBP) …..(2) (7^2+x^2-z^2)/(2*7*x)=cos(<QBR) …….(3) Squaring (1) and (2) and adding up and using (1) x^2*((49-z^2)+y^2)^2+y^2*((49-z^2)+x^2)^2=196*x^2*y^2 x^2*(49-z^2)^2+2*x^2*y^2*(49-z^2)+x^2*y^4+y^2*(49-z^2)^2+2*x^2*y^2*(49-z^2)+x^4*y^2=196*x^2*y^2 (X^2+y^2)*(49-z^2)^2+4*x^2*y^2*(49-z^2)+x^2*y^2*(x^2+y^2)=196*x^2*y*^2 z^2*(49-z^2)^2+196*x^2*y^2-4*x^2*y^2*z^2+x^2y^2*z^2=196*x^2*y^2 z^2*(49-z^2)^2-3*x^2*y^2*z^2=0 canceling out z^2 (49-z^2)^2-3*x^2*y^2=0 (49-z^2)^2=3*7203=147^2 using x^2*y^2=7203 49-z^2=147 or -147 49-z^2=147 ->z^2=-98 leads to no real solution. 49-z^2=-147 ->z^2=196 ->z=14 hence r=7 Area of the semicircle is 1/2*pi*7^2=49/2*pi that’s our answer.

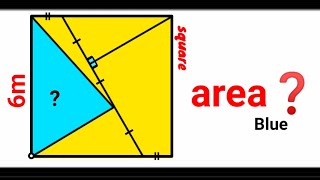
Side of square: s = 6 = 2c + 3r --> c = 3 - 3r/2 Similarity of right triangles: r / b = b / (s-c) r = b² / [6 - (3-3r/2)] r = (2² + r²) / (3 + 3r/2) 3r + 3r²/2 = 4 + r² ½r² + 3r - 4 = 0 r² + 6r - 8 = 0 ---> r = 1,1231 mts Similarity of right triangles: a/2 = 2/r ---> a = 4/r = 3,5615 mts Area of blue triangle: A = ½b.h = ½.s.a = ½*6*3,5615 A = 10,685 m² ( Solved √ )

Similarity of right triangles: a/2 = 2/r --> a = 4/r Side of square: s= 2c + 3r = 6 --> c= ½(6 - 3r) s= a+r+c= 4/r+r+c > c= 6- 4/r -r Equalling: ½(6 - 3r) = 6 - 4/r - r 6 - 3r = 12 - 8/r - 2r r - 8/r + 6 = 0 r² + 6r - 8 = 0 ---> r = 1,1231 mts Height of blue triangle: a = 4/r = 3,5615 mts Area of blue triangle: A = ½b.h = ½.s.a = ½*6*3,5615 A = 10,685 m² ( Solved √ )

Original and impressive ! Here is another method : x^2*y^2=7203 ; then x*y=49*sqrt(3) x^2+y^2=4*r^2 QB^2=(xQ-xB)^2+(yQ-yB)^2 (in an orthonormal repair where P is the center, for example) xQ=2*r*cos(60°) then xQ=r yQ=2*r*sin(60°) then yQ=sqrt(3)*r xB=BR*cos(60°-a) with BR=x and cos(60°-a)=BR/PR=x/(2*r) then xB=x^2/(2*r) yB=BR*sin(60°-a) with BR=x and sin(60°-a)=PB/PR=y/(2*r) then yB=x*y/(2*r) QB^2=(xQ-xB)^2+(yQ-yB)^2 7^2=(r-x^2/(2*r))^2+(sqrt(3)*r-x*y/(2*r))^2 4*49=(2*r-x^2/r)^2+(2*sqrt(3)*r-x*y/r)^2 196=4*r^2-4*x^2+x^4/r^2+12*r^2-4*sqrt(3)*x*y+(x*y)^2/r^2 196+4*sqrt(3)*x*y=(16*r^2-4*x^2)+(x^4+(x*y)^2)/r^2 196+4*sqrt(3)*49*sqrt(3)=4*(4*r^2-x^2)+x^2*(x^2+y^2)/r^2 4*196=4*y^2+4*x^2 196=x^2+y^2 196=4*r^2 49=r^2 A(semicircle)=1/2*Pi*r^2 A(semicircle)=49/2*Pi m²

Hello. Similar method than you : (with your notations) Quite similar to you till 7:20 to find the obvious values : 3*y=6 then y=2 z=3*r (with z=3*r=6-2*QR=6-2*c then c=3-3/2*r) We can express "cos(x)" in the right-angled triangle with hypotenuse = TU : cos(x)=r/b=r/sqrt(r^2+y^2)=r/sqrt(r^2+4) We can express "cos(x)" in the right-angled triangle RSV : cos(x)=RS/RV=b/RV=b/(QV-QR)=b/(6-c)=b/(6-(3-3/2*r))=b/(3+3/2*r)=sqrt(r^2+4)/(3+3/2*r) cos(x)=r/sqrt(r^2+4)=sqrt(r^2+4)/(3+3/2*r) r*(3+3/2*r)=(sqrt(r^2+4))^2 3/2*r^2+3*r=r^2+4 3*r^2+6*r=2*r^2+8 r^2+6*r-8=0 r=sqrt(17)-3 Blue area=6/2*(6-(r+c)) =3*(6-(3-1/2*r)) =3*(3+r/2) =3*(3+sqrt(17)/2-3/2) =3/2*(3+sqrt(17))

Nice, many thanks, Sir! φ = 30° → sin⁡(3φ) = 1 ∎ABCD → AB = AR' + R'J' + J'H' + H' S' + BS' = a + b + b + b + a = 6 = BC = BF' + E'F' + CE' = 2 + 2 + 2 = CD = DR + RJ + JH + HS + CS = a + b + b + b + a = AD = AF + EF + DE = 2 + 2 + 2; area ∆ AQD= ? RS' = RP + PQ + S'Q = k + k + k; sin⁡(S'QA) = sin⁡(RPC) = 1; PAQ = QAS' = δ sin⁡(S'QA) = sin⁡(RPC) = 1 → APS' = 2δ → AP = AS' = 6 - a; b < a < 2; CRQ = θ ∆ AJ'P = ∆CQF' → AJ' = CH = a + b; J'P = 4; sin⁡(AJ'P) = 1; AP = 6 - a 2a + 3b = 6 → b = (2/3)(3 - a) → (6 - a)^2 = 16 + (a + b)^2 → a^2 - 15 = -18 → a1, a2 = (3/2)(5 ± √17) → a < 2 → a = (3/2)(5 - √17) → b = (2/3)(3 - a) = √17 - 3 → a + b = (1/2)(9 - √17) → 6 - (a + b) = (1/2)(3 + √17) → area ∆ AQD = (3/2)(3 + √17) btw: sin⁡(2δ) = (1/6)(√17 + 1) → cos⁡(2δ) = (1/6)(√17 - 1) → tan⁡(2δ) = (1/8)(9 + √17) tan⁡(θ) = (1/4)(√17 + 3) → sin⁡(θ) = (√3/24)(√17 + 3)√(7 - √17); k = (√6)√(5 - √17)

My solution Is (9+3sqrt17)/2 solved in this way: The height of triangle PTU is 2 and it is easy to see if you extend the height above perpendiculary to QV side. You get two similar right triangle whose hypotenuses are b and 2b. Tracing the perpendicular from R to PW side we get two similar triangle having angle in U in common, whose hypotenuse are 3b and b, and the two major legs 6 and 2, so we can write by similarity: 6 : 2 = (6 - 2c) : r r = (6 - 2c)/3 a = 6 - c - r = 6 - c - (6 - 2c)/3 a = (12 - c)/3 = 4 - c/3 now we can find c applying Euclid's theorem on PTU 2² = (6 - 2c)/3 * (12 - c)/3 c² - 15c + 18 = 0 c = (15 - 3√ 17)/2 a = 4 - 1/3*(15 - 3√ 17)/2 = (3 - √ 17)/2 area = 1/2*6* (3 - √ 17)/2 = (9+3sqrt17)/2

Angles BAD and BCD are equal because they tend the same chord BD. Setting BAD = BCD = alpha and BD = BC = x and applying sines law on BCD: x/sin alpha = 4/sin(180-2alpha) and being sin(180-2alpha)=sin 2alpha x/sin alpha = 4/2sin alpha cos alpha cos alpha = 2/x Considering ABD 5/2 = 2R*cos alpha 2R = 5/4x applying pythagorean theorem on ABD (5/2)² + x² = (5/4x)² x = 10/3 2R = 5/4*10/3= 25/6 R = 25/12 area = 625/144 pi

Prolongamos BO y corta la circunferencia en E---> DE=2,5---> EDB es simétrico de ECB respecto al diámetro BE---> BE y CD se cortan en F---> CF=FD=4/2=2---> FE=√(2,5²-2²)=3/2 ---> Potencia de F respecto a la circunferencia =2²=(3/2)BF---> BF=8/3---> BE=(8/3)+(3/2)=25/6---> Radio =r=25/12---> Área del círculo =(25/12)²π =625π/144 u². Gracias y saludos.

I obtained the same answer by the same method. It took me about a minute to solve it.

Great job it's so difficult but will trying more and more

α + 2β = 90° sinβ = 2,5/2R = 5/4R cosα=4/2R=2/R=cos(90°-2β)=sin2β Dividing and cancelling "R" : sinβ/sin(2β) = 5/8 = 1/(2cosβ) cosβ= 4/5 --> Pytagorean triplet 3-4-5 !!! R = ½*2,5*5/3 = 25/12 cm A = πR²= 625π/144 cm² (Solved √)

∆ ADB → AB = 5/2; BD = v; AD = AO + DO = r + r; ∆ BCD → BC = v; CD = CP + DP = 2 + 2 sin⁡(CPB) = 1 = sin⁡(DBA); AO = BO = CO = DO = r; AOB = δ = DOP → ODB = DBO = δ/2 = OBC = BCO → DOC = 2δ → DOP = POC = δ → sin⁡(δ/2) = 5/4r = 2/v → v = 8r/5 → cos⁡(δ/2) = v/2r = 4/5 → sin⁡(δ/2) = 3/5 = 5/2r → r = 25/12 → π ≈ 22/7 → πr^2 ≈ (11/14)(25/6)^2

α + 2β = 90° sinβ = 2,5/2R = 5/4R cosα=4/2R =2/R=cos(90°-2β)=sin2β Dividing and cancelling "R" : sinβ/sin(2β) = 5/8 = 1/(2cosβ) cosβ = 4/5 --> sinβ = 3/5 Returning above: 2R = 2,5/sinβ = 2,5*5/3 =25/6 R = 25/12 = 2,0833 cm Area of circle : A = πR² = 625π/144 = 13,635 cm² ( Solved √ )

I've bookmarked this one for later as it's a bit advanced for my current level. I tried comparing two right triangles formed by Thales Theorem which both had 4r^2 as d^2, and then I looked into the formed cyclic quadrilateral which had 4 and 2.5 as opposite sides 2r as a diagonal, and two right angles opposite from each other. It all became too confusing. A few more months and I reckon I will be figuring it out better.

Is this reasoning ok? The perpendicular bisector OE of the chord CD must pass through B since BC=BD. We have now 3 rt angle triangles namely ABD, BED, and OED. Apply Pythagoras relation to each of them and solve for the value of the radius.

Let radius of circle; AO = OD = r. Let BC = BD = c. Then since AO is a diameter, angle ABD = 90 degrees. Also angle BAD = angle BAC (we'll name the angle theta) since they are subtended on the circumference by the (same) arc BD. For the right angle triangle ABD, we get cos(theta) = (2.5/2r). For isosceles triangle CBD we get cos(theta) = 2/c (explanation draw the perpendicular (also the median and the altitude) from B to the line CD to intersect the line at E; that gives us the triangle BCE with right angle BEC from which we get the cosine of theta). These cosine values are equal so (2.5/2r) = (2/c) or c = 8r/5. Next apply Pythagoras' theorem to triangle ABD to get: (2r)^2 = (2.5)^2 + c^2. Now substitute for c in terms of r and simplify the expression to get r^2 = 625/144. The area requested is pi*r^2 = (625/144)*pi.

Here’s my version with trigonometry to share with. Let <BAD=<BCD=a and AD=2*r where r is the radius of the circle. BD=2*r*sin(<BAD=2*r*sin a ->BD=2*r*sin a ….(1) cos(<BAD)=cos a=AB/AD=2.5/(2*r)->cos a=2.5/(2*r) ….(2) CBD is isosceles triangle, hence BC*cos(<BCD)=CD/2 ->BD*cos a=4/2=2 …(3) Where BC=BD and<BCD=<BAD=a Replacing (1) and (2) to (3) 2*r*sin a*2.5/(2*r)=2 ->sin a=4/5 hence cos a=3/5 replacing to (2) cos a=3/5=2.5/(2*r) ->r=25/12 Area=pi*(25/12)^2=625/144*pi that’s our answer.

Where are you getting 2x and 2y from?

Nice problem!

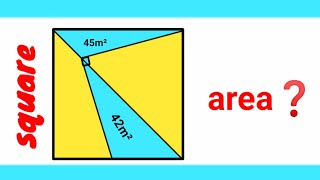
12:00 354/2=177 => => A=x²=v=-(-177)±vʼ((-177)²-16200)= =177±vʼ(31329-16200)=177±vʼ15129= =177±123; A=54 X; A=300 V 15:05 45+42=97 ???

Great job ! We can't do better. I just did like you : * PQRS is a cyclic quadrilateral (inscribed quadrilateral) : Brahmagupta's formula : area=sqrt((s-a)*(s-b)*(s-c)*(s-d)) with s=(a+b+c+d)/2 * PQRS is a tangent(ial) quadrilateral : s=(a+b+c+d)/2=a+d=b+c Then : (s-a)=d ; (s-b)=c ; (s-c)=b ; (s-d)=a area=sqrt(a*b*c*d) area^2=a*b*c*d=a*b*c*(-a+b+c) with a=10*sqrt(3) and b=40*sqrt(3) area^2/(10*sqrt(3))^4=A*B*C*(-A+B+C) with A=a/(10*sqrt(3))=1 and B=b/(10*sqrt(3))=4 and C=c/(10*sqrt(3)) and D=d/(10*sqrt(3)) (1800*sqrt(6))^2/(300^2)=1*4*C*(-1+4+C) (6*sqrt(6))^2=4*C*(C+3) 216=4*C*(C+3) 54=C^2+3*C C^2+3*C-54=0 (C-6)*(C+9)=0 C=6 (because C=-9 is impossible) D=-A+B+C=-1+4+6=9 area=1/2*(a+b+c+d)*r area/(10*sqrt(3))=1/2*(A+B+C+D)*r 1800*sqrt(6)/(10*sqrt(3))=1/2*(1+4+6+9)*r 180*sqrt(2)=10*r 18*sqrt(2)=r 648=r^2 A(circle)=Pi*r^2=648*Pi m²

Here is a simpler method : 0:00 to 2:42 same method than you to find a=b ; angle (PEQ)=angle (QER) Let's call angle (RED)=c Then, angle (BCE)=90°+c and angle(BAE)=90°-(c+2*b) Law of sinuses in triangle BCE : BC/sin(angle(QER))=BE/sin(angle(BCE)) BC/sin(b)=BE/sin(90°+c) 8*k/sin(b)=BE/cos(c) Law of sinuses in triangle BAE : AB/sin(angle(PEQ))=BE/sin(angle(BAE)) AB/sin(b)=BE/sin(90°-(c+2*b)) 10*k/sin(b)=BE/cos(c+2*b) (8*k/sin(b))/(10*k/sin(b))=(BE/cos(c))/(BE/cos(c+2*b)) 4/5=cos(c+2*b)/cos(c) EP=ED*cos(c+2*b) ER=ED*cos(c) EP/ER=cos(c+2*b)/cos(c) EP/ER=4/5 Then, same method than you, from 10:50 to the end. A|EPQ|=1/2*EQ*EP*sin(b) A|EQR|=1/2*EQ*ER*sin(b)=200 cm² A|EPQ|=EP/ER*A|EQR|=4/5*200=160 cm²

0.5yx=45 0.5(x-y)(x-2y)=42

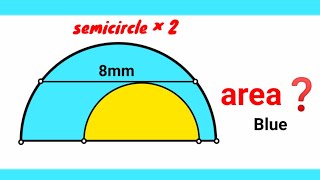
A = ½(¼πd²) = ⅛π8² = 8π mm² (Solved √ ) Diameters of both semicircles are not given, we can modify these, and the original conditions are still being fulfilled. If we modify the not given diameter of yellow semicircle to zero, then the chord "8" becomes the diameter "d" of that blue semicircle, and this is the required area.

A = ½(¼πc²) = ⅛π8² = 8π mm² (Solved √ ) Extremely easy !!!! Just need to apply the formula of the circular ring area, respect to the chord, previusly moving the yellow semicircle to the center of the blue semicircle (Which doesn't modify the required area)

You can slide the center of the small semicircle untill it lies on the center of the big semicircle, then applying Pythagorean theorem R^2-r^2=4^2=16. And being semicircles the area is 16/2pi There was also a logical approach: you can shrink the small semicircle untill its radius =0 then the chord of 8 is the diameter and area semicircle is 16/2pi again 😊

Problem was too lengthy,but some new concepts are learned

Los dos segmentos interiores ortogonales se cortan sobre la diagonal del cuadrado y tienen la misma longitud → Trazamos una línea horizontal y otra vertical por ese punto común de la diagonal, que equidista una longitud "a" de los lados superior e izquierdo del cuadrado, quedando éste dividido en cuatro celdas rectangulares, cuyas superficies son→ celda superior izquierda =a² ; celda superior derecha =2*45-a²=90-a²= celda inferior izquierda ; celda inferior derecha =[(90-a²)/2]+42+42+[(90-a²)/2]=174-a² → a²*(174-a²)=(90-a²)*(90-a²) → a=3√3≈5,19615 → Área del cuadrado = Suma áreas de las cuatro celdas =2*90+174-2a² =354-2(3√3)² =300 m². Gracias y un saludo cordial.

Nice! ∎ABCD → AB = AQ + QT + BT = k + k + (a - 2k) = CD = CP + DP = (a - k) + k = BC = BW + CW = (a - k) + k = AD = AS + DS = (a - k) + k PQ = PM + QM → DP = PM = SM = DS = AT = k → area ∆ DMP = area ∆ DSM = k^2/2; area ∆ CDM = 45 → area ∆ CPM = area ∆ TMQ = area ∆ MWC = 45 - k^2/2 area ∆ BMT = 42 = (1/2)(a - 2k)(a - k) ∆ CDM → (1/2)ak = 45 → k = 90/a → a - k = (1/a)(a^2 - 90) → (1/2)(a - k)(a - 2k) = 42 → (a - k)(a - 2k) = 84 → a^2 + 2(90/a)^2 = 354 → x ∶= a^2 → (x - 177)^2 = (123)^2 → x1, x2 = 177 ± 123 → x1 = 300; x2 = 54 < (42 + 45) → a^2 = 300 → a = 10√3 → k = 3√3 → (a - k) = 7√3 → BD = a√2 = 10√6 → DM = k√2 = 3√6 → BM = 7√6 → MQT = θ → sin⁡(θ) = 7√58/58

Según fórmula de Heron: Área de PQS =6√11=19,8997---> Altura respecto a PS =3√11/2---> Proyección horizontal de PQ=a=½ ; Área de PRS =21√15/4---> Altura respecto a PS =21√15/16---> Proyección horizontal de SR =b≈5,5602... ---> Proyección horizontal de QR =8-a-b≈ 4,3125. ; Proyección vertical de QR =21√15/16 - 3√11/2≈0,10826---> QR =√(4,3125²+0,10826²) ≈4,3138. Gracias y saludos

Cosine rule: c²=a²+b²-2ab.cosα cosα = (a²+b²-c²)/(2.a.b) Angle PSQ: cosα₁ = (8²+9²-5²)/(2*8*9) α₁ = 33,5573° Angle PSR: cosα₂ = (8²+6²-7²)/(2*8*6) α₂ = 57,9100° Angle QSR: α = α₂ - α₁ = 24,3527° Triangle QSR: r² = 9²+6²-2*9*6*cosα r = 4,3138 cm ( Solved √ )

Very interesting, many thanks, Sir! Here an old fashioned way finding roots (√): φ = 30° → sin⁡(3φ) = 1; ∆ PSQ → PS = 8; QS = 9; QP = 5; QPS = θ ∆ QPR → QP = 5; RP = 7; QR = r = ? QPR = α ∆ RPS → RPS = β = θ - α; PS = 8; RS = 6; RP = 7 → ∆ PSQ → law of cosines → cos⁡(θ) = 1/10 → sin⁡(θ) = 3√11/10 ∆ PSR → law of cosines → cos⁡(β) = 11/16 → sin⁡(β) = 3√15/16 → cos⁡(α) = cos⁡(θ - β) = cos⁡(θ)cos⁡(β) + sin⁡(θ)sin⁡(β) = (1/10)(11/16) + (3√11/10)(3√15/16) = (1/160)(11 + 9√165) → r^2 = 25 + 49 - 2(5)7cos⁡(α) = (9/16)(123 - 7√165) 144 < 165 < 169 → 165 = (13 - x)^2 = 169 + x^2 - 26x ≈ 169 - 26x → x = 2/13 → 13 - 2/13 = (1/13)(169 - 2) = 167/13 ≈ √165 → r^2 = (9/16)(123 - 7√165) = (9/16)(123 - 7(167/13)) = (9/4)(5/2)(43/13) → r = (3/2)√5590 → √5590 = ? → 4900 < 5590 < 6400 → (70 + x)^2 = 5590 ≈ 4900 + 140x → x = 69/14 → 70 + x = 70 + 69/14 = (1/14)(14(70) + 69) = 1049/14 → (1049/14 - x)^2 = 5590 ≈ (1049/14)^2 - 1049x/7 → x = (4761/196)(7/1049) ≈ 162/1000 = 81/500 → 1049/14 - x = 1049/14 - 81/500 = 261683/3500 ≈ 74,76657 ≈ √5590 → r= (3/4)(√430/√13) = (3/52)√5590 = (3/52)(261683/3500) ≈ 4,313456 → 3√(123 - 7√165)/4r = 1,000093882 (looks like a good approximation 🙂)

We use AI Cachi theorem in triangle PSR and find cosα= (8²+6²-7²)/(2*8*6)=17/32. Then we apply it in triangle PSQ and find cosβ= (8²+9²-5²)/(2*8*9)=5/6. So sinα=√11/6 and sinβ=7√15/32. Hence x²=6²+9²-2*6*9*cos(α-β)=117-108*((5/6*17/32)+(√11/6*7√15/32))= (1107-63√165)/16. Hence x= (3√(123-7√165))/4.

I used right triangles and it became very convoluted. I had perpendiculars from the base (8) up to Q and R from corresponding points on the base. I then set up two sets of equations to find the dimensions of the two right triangles created. I then calculated the difference in heights for the short lengths down from Q and the other length I projected up from the base line as the gap between the two perpendicular points. The redline was then calculated by Pythagoras. It was very complex. I don't doubt your way was better, but I'm not yet at a level where I could understand all of it.

Interesting problem, I think it was presented some time ago but now it's solved by a different method. If we can't solve it by construction, then the formula helps. I will look into it to see if I get a different idea for solving it.

Let D be where 2a segment and a segment divide. Then, by Intersecting Chords Theorem, (r+a) * (r-a) - 2a * a --> r^2 - a^2 = 2*a^2 --> r^2 = 3*a^2 --> r = √3a. So, OC = √3a and OD=CD=a. Then DCO=DOC = s and ODC=180-2s. Only way possible is s=30 and ODC=120. Now look at AOC triangle: OA=OC=r=a√3. Then OAC=OCA=30 --> AOC = 180-2*30 = 120. But DOC=s=30 --> AOD = 120-30 = 90. Now AO=BO=r. Then OAB=OBA=x but AOB = 180-AOD = 180-90 = 90 --> 2x = 180-90 = 90 --> x=45.

I got the same answer. Let F be midpoint CE -> CF=100/82=50 --> AD = √ (150^2 + (50√3) ^2) = 100√3 --> tan (DAE) = 50√3/150 = √3/3 --> ADE=30 --> FDA = 90-30 = 60. But CDE equilateral ---> ,FDE = 60/2 = 30 --> ADE = 60+30 = 90 ---> ADP] = AD*DP/2. Now DP = DE/2 = 100/2 = 50 ---> [ADP] = 100√3 * 50/2 = 2500√3 = 4330 mm^2.

I obtained Area=8.90619. Probably I made an arithmetic error somewhere.

I got the same answer, though at first I forgot to multiply both areas by sin 60. When I saw the video, I noticed I had forgotten to multiply both areas by this factor.

Only a radial line can bisect AC. Let center be O. Since CD parallel to BS, then OS/4 = R/2R --> OS = 2 --> R = OS + 1/2 = 5/2. Then AD = 2R = 5. Since ACD=90 because it is suspended by the diameter at the circumference, AD=5, and CD=4, then AC=3 by Pythagoras. Then [ACD] = AC*CD/2 = 3*4/2 = 12/2 = 6 sq. units. I'll watch your video to see how it's solved.

Triangles ASO and ACD are similar and in a 2 to 1 ratio. Therefore , SO is 2 and the radius is 5/2 and diameter is 5. Side Ac is thus 3 (3:4:5 triangle) Thus, area of triangle is 3×4/2 = 6 sq.units

Si AC=a---> (a/2)²=(½)*(4+½)---> a=3---> Área ACD =4*3/2=6 u². Gracias y saludos

Intersecting chords theorem: (R+a)(R-a)=2a.a R²-a²=2a² R²+a²=(2a)² --> Pytagorean formula This means that triangle AOP is a right triangle !!! Therefore, isosceles triangle AOB also is a right triangle : X = ½90° = 45° ( Solved √ )

φ = 30° → sin⁡(3φ) = 1; ∆ QPV → PV = PA + TA + TV = 7 + 7 + 6 QV = QS + VS = (t - n) + n; PS = k = PR + SR = k/2 + k/2; ST = 6 = SG + TG = 3 + 3 QA = QR + RA = x + RA; VQA = AQP = TVS = VST = δ → ATS = 2δ SPA = ASP = SAG = GAT = α → SAT = 2α → ATG = GSA = 2δ sin⁡(PRQ) = sin⁡(AGS) = sin⁡(TSP) = 1; QA = QR + AR = x + 3; x = ? ∆ ATG → sin⁡(α) = cos⁡(2δ) = 3/7 → cos⁡(α) = cos⁡(2δ) = 2√10/7 → tan⁡(α) = √10/5 ∆ PTS → PS = k = √160 = 4√10 → k/2 = 2√10 → tan⁡(δ) = k/2x = √10/5 = 2√10/x → x = 10 → (t - n) = QS = 2√35 → SV = n = 12√35/7 → QV = t = 26√35/7 → QP = QS = 2√35 → sin⁡(α) = 3/7

Triangle AOP is a right triangle, because OP=PC. Therefore, AOB is an isósceles right triangle x = (180°-90°)/2 = 45° ( Solved √ )

φ = 30° → sin⁡(3φ) = 1; BP = BO + PO = r + a; AC = AP + CP = 2a + a; AO = BO = CO = r sin⁡(POA) = 1 → AO = r = a√3 = BO → OBA = x = 3φ/2 → ACO = OAC = COP = PCO = φ → OBA + BAO + OAP + ACO = 3φ/2 + 3φ/2 + φ + φ = 5φ → CBO = OCB = φ/2 → ACB = 3φ/2; CBA = 2φ; BAC = 5φ/2

At 3:20, construct OA. OA and OC are both radii of the same circle, thus are equal. ΔAOC is, therefore, an isosceles triangle, the angles opposite the equal sides are equal, so <OAC = <OCA = 30°. Consider ΔAOP. <OAC = <OAP = 30°, <APO = 60°, leaving 90° of the 180° sum of interior angles for <AOP. Extend OP to intersect the minor arc AC. <AOP is a central angle, so the arc it intersects equals its measure, or 90°. <ABP = X is an inscribed angle intersecting that 90° arc, so has half the measure of the arc, or 45°. So, X = 45°, as Math and Engineering also found.

way too complicated: same base, same height = same area 🙂 φ = 30° → sin⁡(3φ) = 1; AE = 4a = 200mm → a = 50mm BAC = ACB = DCE = CED = 2φ; DE = 2a = DP + EP = a + a sin⁡(EDA) = 1 → DAE = φ → DA = 2a√3 = h → area ∆ AEP = area ∆ APD = (1/2)area ∆ AED = a^2√3 ≈ 4330(mm)^2 btw: PAE = α → sin⁡(α) = √39/26; DAP = β → sin⁡(β) = √13/13