วีดีโอ

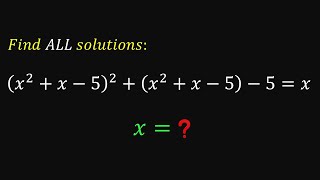
Let a+b+c+d=s, The given expression will become a²/(s-a)+b²/(s-a)+c²/(s-a)+d²/(s-a) Now add and subtract a+b+c+d and pair each term, a²/(s-a)+a=sa/(s-a) Take s common and the rest will become 1 you will get s-s=0

What's the name of the method you used to find the roots of the cubic eqn?

Thank you so much easy maintindihan

👍I also have a problem of this type factorise x^6 + 5x^3+8 Here we can write 5x^3 = - x^3 - 3 (x^2)(-x)(2)

Great video!🔥 A question: is it wrong to start from the internal absolute value to solve this equation?🇮🇹👋

Ez method here Multiply both sides with a+b+c+d , now multiply like this A²+A(b+c+d), for b multiply like this B²+B(a+c+d) and so on. If u look carefully ull see that if u divide every individuals of the nominator with the denominator ull get A²/b+c+d +A and so on Now just cancel out the lhs's a+b+c+d with the RHS's a+b+c+d and u will have an answer 0. This seemed ez for me so I shared this method 😅

Increíble

Nice solution. Other approach: x=y²+y-5 (1) y=x²+x-5 (2) After subtracting (2) from (1) we get x-y=y²-x²+y-x y²-x²+2(y-x)=0 (y-x)(y+x)+2(y-x)=0 (y-x)(y+x+2)=0 hence y=x or y=-2-x After substitution y=x into (2) we get quadratic x²-5=0 with real roots x=±√5 After substitution y=-2-x into (2) we get quadratic x²+2x-3=0 with real roots x=-3 or x=1

What is the name of the software that you are using?

✨Magic!✨

Nice solution, I would really appreciate if someone could tell me a more simple way to solve this question, just by using common sense! (Ps: I believe that these solutions exist for any given question, It's just that sometimes we are not able to see it directly)

❤

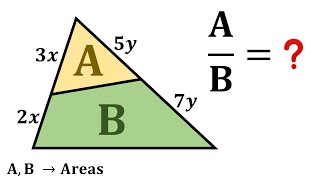
Theorem for Ratio of Areas of Shapes having Common Angle says that Ratio of Areas is equal with Ratio of products of the adjecent sides. So (A)/(A+B)=(3x•5y) /(5x•12y) so (A)/(A+B)= (3•5)/(5•12)=3/12=1/4 so 4•A=1•(A+B) so 3A=B hence A/B=1/3.

Area of small triangle= (1/2) (3x)(5 y) sin theta Area of large triangle= (1/2)(5x)(12 y) sin theta Ratio between areas of triangles = 1:4 hence A:B = 1:3 But solution given in video is very basic and a good example for junior level students to enhance their geometrical concepts

Beautiful 😍 thx deeply 😊

I would do it shorter. 10^36/9^37 = (10/9)^36/9 > (10/9)*36/9 = 40/9 > 1

There is an easier way. A theorem says that each of the vertical sides of a right-angled triangle is the geometric mean of its projection on the hypotenuse and the whole hypotenuse. So, we can apply this to the triangle that is formed with the intersection of the segment x and the semicircle and the diameter of the semicircle. The projection of the segment x is one of the sides of the rectangle whose area we are looking for. Too bad I cannot attach a schematic here.

Buenos días Señores: Zahien (MATHics), reciban un cordial saludo, Gracias por este interesante ejercicio de límites, su explicación muy comprensible. Por favor podían hacer ejercicios de límites con la aplicación de logaritmos. Anticipo mis agradecimientos por la atención que se me brinde. Éxitos.

(8+6)/4=3.5

Does this formula work if the chords aren't perpendicular?

I directly divided Nominator and Denominator with x#0, because if x=0 then 1/1=2/3 impossible. The Equation becomes (x-1+1/x)/(x+1+1/x)= 2/3. Let x+1/x=y so we get (y-1)/(y+1)=2/3 so 3•(y-1)=2•(y+1) so 3y-3=2y+2 so 3y-2y=2+3 so y=5 so x+1/x=y=5.

Domain is x such as x >= 0. x=0 is an obvious solution so √(x-√x)=0. Also If parameter A=1 then we have the Quadratic Equation x^2-x=0 so x•(x-1)=0 so x=0 or x=1. We have seen before the case x=0. If x=1 then √(x-√x)=√(1-√1)=√0=0. If x>0 then √x>0 so if we divide by √x=y>0 we proceed exactly as you do.... getting finally √(x-√x)=√(A-1) and A>1. Note:From Quadratic y^2 -y-A+1=0 we have D>=0 so 1^2+4•A-4>=0 so 4•A>=3 so A>= 3/4. Combining with A>1 we get A>1. Also must x>or=√x so x^2> or= x so x^2-x >or = 0 so x>or=1. The Case x=1 is giving 1-A=A-1 so 2A=2 so A=1 we have seen in the begining. Now we had only A>1.

Great!!!

Where was it proven that the inner circle's lines' length is also 1?

since x^2 = । x।^2 we can write (।x।+4) (।x।-3) = 0 now ।x। >= 0 hence first factor can't be zero. By second factor we get x= 3 , -3

If the radius of the big circle is 3 units, then your figure is not drawn to scale, and is deceptive. Also, you did not challenge your viewers to solve the problem with only the available information, while also warning them that the figure is not drawn to scale. That would have been a fair challenge.

I did know the radius of the big circle was 3, but it was a guess. Thank you for teaching me how to prove my answer was correct

good

I considered the projection of the radius of measure 1 of the inner circle on the radius of the quarter circle and added the diameter 2 of the semicircle obtaining 3, then I proceeded as you did. I found your geometric demonstration of the radius of measure 3 fabulous: you have a stimulating mind!🔥🔥🔥👋🇮🇹

Thank you very much for stimulating my mind with your problem: it makes for a good start to the day.😄

it is 1+7+19.... subract 1 from each term now ,0+6+18+36.....+10 take 6 as common 6(0+1+3+6+10+15+......)+10 6[0+1+3(1+2)+5(2+3) +7(3+4)+9(4+5)]+10 6(1^2+3^2+5^2+7^2+9^2)+10 6(1+9+25+49+81)+10 6(165)+10 990+10 1000

Very good problem Solving only with Pythagoras theorem 👍

Are you sure that you want ask what you ask? :) If you would ask the value of x-3/(x+4) than you will get 1 that much more prettier than irrational radical mess.

I worked out .0209375 trial and error

Nice approach

What is the software you use for you videos? The animations are very good! Great job on all your videos!

f (x) = 3 x (x-1) +1 S (x) = 3 (x+1) x(x-1) /3 +x + c S (x) = (x+1) x(x-1) + x + c now S(1) = f(1) hence 1+c = 1 or c= 0 S(x) = (x+1) x (x-1) + x S(10) = 11×10×9+10 = 1000 similarly if f(x) = x then S(x) = (x+1) x/2 + c S(1) = f(1) gives c = 0 hence S(x) = x(x+1)/2

A simple question, the 4 cm and the 3 cm lines are parallell yes or no ? If they sre parallel then : The 2 cm (equilateral triangle) divide the 4 cm line in the middle and you can project the lower 2 cm of the 4 cm line to the bottom of the 3 cm line. Now you have a right triangle with 5 cm hypotenuse. A right triangle withhupotenuse 5 which known as a pythagorean triple triangle of 3 4 5 (3²+4² = 5²). From this the square side must be 4 and hence the area is 16cm²

D= (-3)^2-4*1*(-7) = 9+28 = 37 so x= (-3+ sqrt 37) / 2. Then x + (3/x+4) = x * (x+4) / (x+4)+3 / (x+4) = ( x^2 + 4x +3 ) / ( x + 4 ) = (x^2+3x+x - 7+10) / (x+4) = (0+x+10) / (x+4) = (x+10) / (x+4) = (x+4+6) / (x+4) = 1+6 / (x+4) = 1+6 / ((-3+ sqrt37)/2) + (8/2 )= 1+12 / (5 + - sqrt37 ) = 1+12 * ( 5 - +sqrt37) / ((5+ - sqrt37) * (5 - +sqrt37) = 1+12* (5 - +sqrt37) / (25-37) = 1+ 12* ( 5 - +sqrt37) / (-12) = 1 - (5- +sqrt37) = 1-5+ -sqrt37= - 4+ - sqrt37

80º

Can you suggest some books from where I could learn and practice Algebraic Manipulation? It would be really helpful for me.

Thanks for sharing.

Trick from my college days (1968). lim(-infinity)(f(x)) = lim(+infinity)(f(-x)). So lim(-infinity)(sqrt(4x^2-x)/(x+2))) = lim(infinity)(sqrt(4(-x)^2-(-x))/(-x+2))).😎

awesome 👍

Galing-galing. Love these q&a

How do you know that when you move the yellow line to that point, keeping the same angle it will intersect the corner of the square? If you cannot prove, this is is not a solution at all

Nice in general if r , a , b are radii of desired circle and other two circles respectively then 1/√r = 1/√a+1/√b here a = 9 , b = 9/4 1/√r = 1/3+2/3 = 1 hence r = 1

Nice solution. This equation (as a quartic) has four roots - the other two are complex and can be found as follows: x=y²-6y+12 (1) y=x²-6x+12 (2) After subtracting (2) from (1) we get x-y=y²-x²-6y+6x (y-x)(y+x)-5(y-x)=0 (y-x)(y+x-5)=0 hence y=x or y=5-x After substitution y=x into (2) we get quadratic x²-7x+12=0 with real roots x=3 or x=4 After substitution y=5-x into (2) we get quadratic x²-5x+7=0 with complex roots x=(5+i√3)/2 or x=(5-i√3)/2