Optimization Problem: Largest Rectangle Inscribed in an Ellipse
ฝัง
- เผยแพร่เมื่อ 15 พ.ย. 2024
- Optimization Problem: Largest Rectangle Inscribed in an Ellipse
📐 Maximize Your Geometry Skills! 📐
In this video, we tackle a calculus optimization question: finding the largest rectangle that can be inscribed within the ellipse defined by the equation (x^2) / 4 + (y^2) / 9 = 1
What You’ll Learn:
Understanding the Ellipse: Get a clear overview of the ellipse and how it relates to the rectangle we want to inscribe.
Setting Up the Optimization Problem: Learn how to formulate the area of the rectangle in terms of the ellipse’s dimensions.
Applying Calculus Techniques: Follow along as I derive the area function, find critical points, and determine the dimensions of the rectangle that maximize the area.
Why Watch This Video?
Ideal for Students: Perfect for high school and college students looking to strengthen their understanding of optimization in calculus.
Clear Explanations: Enjoy step-by-step guidance that makes complex concepts easy to grasp.
Real-World Applications: Discover how these optimization principles can be applied in various fields, including engineering and design.
📈 Engage with the Content:
LIKE this video if it helps enhance your understanding of optimization!
SHARE with friends or classmates eager to learn more about calculus!
SUBSCRIBE for more insightful math tutorials, problem-solving strategies, and educational resources!
#Optimization #Ellipse #Calculus #MaximizingArea #Mathematics #MathTutorial #EducationalContent #LearningCalculus #ProblemSolving #HighSchoolMath #CollegeCalculus #RealWorldApplications #Geometry
![How to Solve ANY Optimization Problem [Calc 1]](http://i.ytimg.com/vi/cUMvwG7wvzM/mqdefault.jpg)
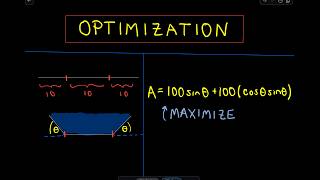
From equation of an ellipse: a=2, b =3:
by observation the area of the rectangle inscribed inside the ellipse is 2*a*cos(theta) * 2*b*sin(theta).Which is 4*a*b*sin(theta)*cos(theta). since 4*a*b are constants of the ellipse we don't really need to care about them (as the ellipse changes as long as the area of the rectangle has a*b in its formula, the rectangle will also change accordingly). What will determine the biggest (or largest area) rectangle will be the biggest possible value of cos(theta)*sin(theta). Even if you're bad at math, just plug in values for theta and see what the biggest value of (sin(theta*cos(theta)) comes to. you will notice the largest value is 0.5 @ theta = 45 degrees... so largest AREA of rectangle inscribed in an ellipse = 4*a*b*0.5 = 2ab.
very cool
Hell nah man. My professor gave a problem like this for an exam tonight except it was an ellipsoid and we had to maximize a rectangular box with in it's constraints. Talk about PISSED. Hard ass exam.
I think it is easier to consider the square of the area . After substituting y in terms of x in the equation of square of area, we can take the derivative of square of A with respect to x and set it to zero, the critical values of x can still be obtained . One of the advantages of doing this is that the differentiation is more simple. The other is that there is no need to discuss the numerator of the derivative as in your method.
hate the sharpie sound, love the learning
Please make a video of cauchy-riemann equation
Your videos are really helpful
I think you can just set the area function equal to another function but it is squared to remove the square root in order to make differentiation easier.
Amazing work you just made my studentlife much easier ! 👍
B. J jjjn ok j ki j. J jj j jj jjj jojojj jj jjo
Jnj. J jj. Jnn. Join j j jj joj. J jj ijjbnjjj j jjjj BB jojjjj j😊n. Joj j. N j. Jjj jnj book j. Ki bi jn j. J boo j k j njj jnob ki book jjjj j BB bj jb j. Jjj. J jj jj jj j BB jbj BB jno BB j jj. Bj bbj o. Ji bj jj. Bj k bj n. Jjj. Jb jj jo o j j. Jji bj j jjojj. J BB boo BB j j k j jj. Joi j j boo jj joj. J. J bj j j j j I jo jnbj. Kbjjj j. Jo j jj. J j jjoj bj j j BB bj BB bj o bj j j jj b BB jbj jn. I. J boo njjnj. Jj j j j j jb BB j bj jnni. Jbj j. Jn bj jj j jkbj bj bjj bj j ji. Jj BB jjj j BB j. J jbjb BB. J j. J j b BB jjj. O bj oo jo jjo. J ojjjojj oj
BB b 😊 j. J. BB j j jb jin. BB BB BB j BB j. I. O j jj ji BB bjjo no ib BB BB ji b bj oj. Bj bj. J BB ji oj k. Knoj BB bj I jo j boo ji. Jjjn jj know j. Jjj BB. Oj o j bbq i j BB j j. J. J😊 jj. Jn jjo j. J. O jij j. J. Ok j ooo j oj. J. Ojj o. J. J j j j. Jin BB k. Jj. O BB j BB boo j jij. J BB jj. J jj jo bjjbj jjj book j bbj jj o b BB BB jjj ob BB. O k BB BB obj BB BB I j Joi BB j book. J on bj kbjj kjbbj a jjojjj. Kb j BB bj j BB I BB b BB ji bj bj BB o o jjbbob j oj jj jj j. J BB j BB BB j. Join. J j koj j j. K
Dude, I have a quiz on optimization tomorrow. Perfect timing lol
My students have a test this week over it :)
Good luck on your quiz!
+Taylor S oh noes i have test this week
+Taylor S Dude same, and one of the practice questions was this exact question.
you have saved the life of a Pakistani student!thnx a lot
You have already helped a brazilian student! Many thanks
Guys, take f as 4xy and g has given ellipse equation and use Lagrangian multiplier method i.e F = f + lambda g. It will be pretty ezy✌️
Patrick JMT - that was wow! Your the best !
Very thank you respected sir...
I really enjoy ur content thanks
Thanks brother!
Can't we assume the co-ordinate as (2x, 2y) or (x/2, y/2) in place of (x,y) ?
You are amazing.
thank you for those videos
Isn't this easier with Lagrange Multipliers?
+Jaxkelington Jenkins Yes. Do you happen to be a student of economics by any chance?
nope, Lagrange Multipliers was in my calculus textbook
I believe that your original area equation is incorrect, I think it should be [ A=2x*2y OR A=2(xy)]. Correct me if I'm wrong though.
It's actually A=4xy.
A=4xy so A'=4y+4xy'=0 implies y'=-y/x
(Where A' and y' are the derivatives with respect to [wrt] x)
Differentiate the equation of the ellipse wrt x:
(2x/4)+(2yy'/9)=0 , substitute -y/x for y':
(x/2)-(2y^2/9x)=0, so 9x^2=4y^2 ...(1)
The equation of the ellipse can be simplified to:
9x^2+4y^2=36 ..(2)
Equations (1) and (2) give x=sqrt(2) and y=3/sqrt(2).
After showing that these values of x and y actually yield a maximum area: A=12
super helpful, thank you so much
im confused when you took the derivative of x squared/4 if you use the quotient rule you get 1/16 and derivative of 1 is equal zero I get how you get half but which answer and method is it?
take the co ordinates as (2cos@, 3sin@) then the problem becomes a piece of cake.
lets get thumbs up all the way to 690 bc this is so useful
God I hate fractions. I try to get rid of them as soon as possible. I needed clarity on the "constraint" function, once I get pass that, I'm OK.
You've just helped an Iraqi student :D
:) howdy from USA!
Correction, it should be denominator not numerator. I make a mistake.
sir your emazzing realy i like ur all videos i am from pakistan
Freedom to balochistan soon
or simply 2ab
Who says the rectangle has to be oriented like that? What if I decide its slanted?
It will be the same, the drawing is just for explanation.
+Ibrahim Ismael no it's not the same. if it were a circle it would be the same since you could rotate arbitrarily. but an ellipse has minor and major axis which he's assumed the rectangles edges are parallel to.
I agree with you, but maybe it's because when you make the rectangle taller for ex.
the y increases and x decreases, so it's like inverse relationship that wouldn't change the area.
just point of view
Thank you
You're welcome
I need to do this in one quadrant with a triangle, Idk how
Did you find out, mate? It's been like 2 years.
Thanks
Kill me i got an exam tomorrow at 7am
need help with this problem, Find the dimension of rectangle of maximum Area A that can be inscribed in the portion of the parabola y*2 = 4px intercepted by the line x = a......pls email me with a detailed solution:)
thanks
the concept isnt to hard to get but the calculations are tedious and messy
Just hope priyanka doesn't get fooled lol
1:40 Nice face there :)
wrong!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
an avg indian math student can solve this in 2 mins by squaring the area and then taking the derivative and putting it equal to 0