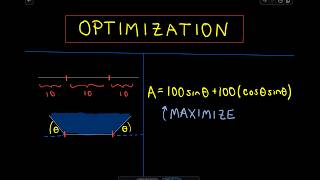
Optimization Problem: Maximizing the Area of a Rectangle Under a Parabola
ฝัง
- เผยแพร่เมื่อ 6 ก.พ. 2025
- ( • Points on Ellipse Fart... )
📏 Explore Optimization with a Rectangle Under a Parabola! 📏
In this video, we tackle an optimization problem: maximizing the area of a rectangle that is bounded below by the x-axis and above by a downward-opening parabola. This classic calculus problem illustrates how to apply optimization techniques to find the largest possible area within given constraints.
What You’ll Learn:
Understanding the Problem: Discover how to set up the rectangle in relation to the x-axis and the parabola.
Setting Up the Area Function: Learn how to express the area of the rectangle as a function of its dimensions.
Finding the Derivative: We’ll guide you through the process of taking the derivative to find critical points where the area is maximized.
Analyzing the Results: Understand how to interpret the results to determine the dimensions of the rectangle that maximize the area.
Why Watch This Video?
Ideal for Students: Perfect for high school and college students studying calculus and optimization.
Clear Explanations: Follow along with detailed, step-by-step solutions that simplify complex concepts.
Real-World Applications: Learn how optimization plays a vital role in various fields, including engineering and economics.
📈 Don’t Forget to:
LIKE this video if you find it helpful!
SHARE with classmates or friends who want to master optimization problems!
SUBSCRIBE for more tutorials, problem-solving techniques, and educational content!
#Optimization #Calculus #MaximizingArea #RectangleUnderParabola #MathTutorial #EducationalContent #LearningCalculus #ProblemSolving #HighSchoolMath #CollegeCalculus #DifferentialCalculus #RealWorldMath #AreaFunction #CriticalPoints







![How to Solve ANY Optimization Problem [Calc 1]](/img/n.gif)
who knew this would still be helping people 16+ years later, thanks man appreciate you more than you know
oh, i knew.... :) glad it helped!
Calculus wouldn't be possible without you, Pat. :)
fax
well, understanding the problem first is the key! then i would draw a diagram. the hardest part (to me) is trying to find the equation that you need to maximize or minimize; this is often the part where you have to be resourceful!
Quick tip: take the second derivative (the concavity) and plug in the critical number(rad 8/3). If the number is positive, then its a min, and if its negative, then it's a max.
My Calculus book (James Steward) has optimization problems that are close to impossible difficulty for Calc 1 students. I wish we could be given problems like this to make sure we get the concept instead of trying to remember a million unimportant trig identities.
same with me. you are so on the point for this.
My favourite lecturer from TH-cam University! :-)
nice! : )
ahhhh the comments... like a wave of happiness at the end of a long day. : )
glad i was able to help
If my teacher had only used the word constraint, that word really is the reason I get the topic now.
Yup. Baby Clara.
TheBetito123 You do know how to make people feel uneasy.
@@clarahav Clara?
@patrickJMT the best part of this video (besides the fact that the material is much easier to follow than in class) is that i can rewind it if i don't comprehend the concept the first time as opposed to raising my hand and disrupting the flow of the class every few minutes. Thanks alot for taking the time to post these, math guru!
by far, the clearest anyone has ever explained math to me. you are my hero.
You are my favorite Professor in Online Class University
You don't apologize for a shameless plug, it's not shameless if you do!
yes, you can use the second derivative test to determine if a critical number is a local max/min value (in most cases)
happy to help :) come back any time!
i guess if you are a math teacher, the math noble prize is constantly yours absolutely no doubt. your usual present in youtube always make me pass my calculus. the first cheque am gonna get in my math career is will be yours. thank you so much Patrick
I'm majoring in middle school education. I've wanted to teach science, but I'm beginning to be more accepting of the possibility of teaching math someday because of all the people you're able to help. There's so much gratitude and relief on your channel.
You are AMAZING. Calculus has never been more clear to me :)
Thank you so much, I want you to know that you're helping a lot of students and that we're all super grateful to have you tutor us!
you not only have a gift in math but you also have a gift of teaching!!!!!!!! you have no clue how much your videos have helped me thank you so much
@china2207 u could show that the derivative is negative or positive by taking a number less than sqrt(8/3) to show the function is decreasing or increasing and a number larger than sqrt(8/3) to show it is increasing or decreasing to justify you have a min or max
@Leninade you can use the second derivative test, yes.
spent 2 weeks in math class not understanding optimization, learned it from just 2 videos of this
OMG! I saw this video last night, (a night before my test), and I swear to you my professor put the exact same problem on the exam except with different numbers! thanks to you I was able to do it without a problem!!! I know you must hear this all of the time but you help more than you know!!!!!
it's amazing how a free short video explains everything than a 80 minute paid college lecture
seems easy. But when i do it....fucking hard.
watwat293 The story of how I found out these Videos doesn't help, you actually have do many examples to figure out how to do it on your own. I usually just use these Videos for reference incase I missed something in class.
Story of my life...
The hardest part is setting up the fucking equation. Hate this part of calc
i feel you
my life in math
You sir just saved my life by teaching me what my BC Calculus test is about tomorrow!
If only you were my teacher! ;-;
you never fail me. This is my second year of calculus (last year was HS Calc, this year AP Calc) and you always make things easier to learn!
Dude, thanks for making it so clear and straightforward! I watched one of your videos and I finally understood the concept! :)
You're not just uploading videos, you're saving some people's lives! (mentally, financially, physically)
God bless this man
Don’t apologize for promoting your website :)❤️ thank you for being our ticket out of calc!!
this is much better than just having to read the book. it sucks not having someone teach you the material.
You have such an easy and simple way of teaching. Thanks man, you will save me through my first year of college.
these videos are the only reason i was able to pass calc 1 ....cant wait to spend hours watching your calc 2 videos this semester lol
You video is helping me learn Calculus a lot smoother! You should post more videos, you really know how to explain the different concepts in an understandable way.
If you are not a math teacher already, you should definitely think about becoming one! Very helpful video!
thank you sir, I came here to understand it a little bit more because I couldnt understand it from my professor. You made it a little bit clearer for me.
teach what you love :) people need good science teachers too!
The fact that you are left-handed makes me really happy.
--a left-handed person
LOL, I watched about 30 of his videos and never noticed until I read your comment ... :-)
You helped so much man! I wish you were my math teacher, you explain things in such a clear and organized manner, keep up the AMAZING work!
You are the reason I'm passing AP Calculus. Thank you for all the help.
You've helped me understand optimization with ease!!! not like others, even my own professor! who make it too complicated! THANK U!
Patrick, you are the man, seriously. You proved that being aware of max/min values, increasing/decreasing test, first,second derivative test all helps. However, i have a question. Is there any way to use the concept of the concavity test in optimization problems and if so, could you possibly demonstrate one that involves such? Once again,you are the man. I definitely will be contributing to your site in the form of a donation.
I cannot express how thankful I am for your videos!
Thanks so much, my Calc teacher doesn't particularly teach... well, anything, and you've been a great help!
I promised myself I would thank you (yet again) if I got an awesome FINAL grade in my calc class!! .... And guess what, I did!! I THANK YOU from the bottom of my heart because it was your videos which truly helped me more than my professor ever did!!! :D THANK YOU PATRICKJMT!! I look forward to using your statistics videos on your website!
I decided to look at this 2 hours before my test although we've never done a problem like it in class before....I just wanted to understand the concept & guess what a problem like this was on my test, YES, thank you.
if the coefficient on the x^2 term is negative, for example:
-x^2, -4x^2 + 7x - 49, -10x^2 + 8x, etc.,
the parabola opens downwards!
I am not able to do one optimization in the James Steward Calculus book for Optimization given the ridiculous difficulty in the problems... So I watch this and continue to Newton's Method...
I hate that book, stupid proofs and useless hard examples.
Bruh i'm here for the same reason. xD The optimization ones are absolutely ridiculous, i can only do ~ 1/8 of them, and i had no difficulty doing the ones before optimization.
@@lerubikscubetherubikscube2813 Same here Lol, honestly Im really just trying to understand bits and pieces of it so I get part marks..
dude same 100%
George Hanna SAME!! We also use James Stewart
@47der yes, rewinding is a good thing :)
Without you I would be failing. Went from like a 65 to an 80 with your help after viewing your videos for just a month, which is a lot for AP Calc. Hopefully I can make it into the high 80's, maybe even the 90's this marking period :)
Used this for Calculus in high school, still using for college :) super helpful, thank you!
I love every single one of your vids, which help me a lot in math (that is my favorite subject to do)!
Yay for patrickJMT helping me in Calculus, and everybody else : )
happy that i could help!
Love you man! Helped me understand before my exam.😅😅👊🏽👊🏽
@patrickJMT Seriously dude., You're helping me out so much for my final tommorow.
thanks for your videos man really helpful. i wish u were my personal tutor for calculus
This is so helpful! I'm in college and I'm using these videos as studying for my final!
Any given topic,i watch your videos. They help. God bless You
everyone 'relearns' algebra as they go.
my suggestion would be to brush up on it over the summer know.
know basic graphs, how to solve a variety of equations involving a variety of functions
You are helping me so much. Keep up the great work man.
lol...You have exam tmmro..thats why u are here...=)
oh man!!!....you are ten times better than my maths teacher
Thankxx bro.
i got perfect on my first calc test thanks to you!!! keep up the great work! these videos really do help :)
no problem
@charminator123456 no, it is there
a= xy is only the area of one side of the rectangle from the y axis. since its a parabola the area on both sides will be the same, so i guess u can multiply it by 2 or double it
@metalmine1 oh, people would still complain
Yes. I'm definitely interested in viewing your video concerning the application of the second derivative test to find max/min values. I would appreciate that greatly. On a more personal note, what would you say to an individual like myself who aspires to obtain a B.S. in math who also has a questionable strength in his foundation( algebra,etc). My foundaton in math can be compared to a removable and jump discontinuous function, too many gaps and holes,lol.
haha awesome, i was doing this exact problem when i felt like checking your vids.. BAM PatrickJMT saves my day.
i was laying on my side when i was thinking about it...
I was literally failing till I found these. Thank you so much!!
so where would u plug in the square root of 8/3 o check if its a maximum or a minimum? by the way u explain so well.
yep! thanks for helping choo!
Can you please do more complicated optimization problems, for example, triangles in circles
idk why i didn't discover this earlier... you're great!
Can you replace my current calculus teacher? Id appreciate it
Ughhh FML my Calc final is at 6pm! Your videos are helpful though!! :)
i love all of your videos, but can you please display the question in the beginning of the problem
YOU JUST SAVED ME FROM CRYING THANK YOU
good video, can do more examples in non linear optimisation and Dynamic optimisation
thanks alot
"heres my shameless plug for my website" haha love it
2(xy) = 2xy
Please write the question the comment box! That would really help. AND THANK YOU FOR ALL YOUR HELP.
Thanks for the video. You should make more, thanks!
i have a video on using the second derivative test to find max/mins if u are interested
Lol "next time: dont watch" I love you Patrick :D you make Calculus feel like the best subject ever :D Im definitely using you in college lol
i am trying!
Thanks so much! I'm studying for my exam and this problem showed up... with different numbers. :D
its becuz xy is the area for the rectangle on the right of the y-axis but there is a rectangle on both sides
thus 2xy since 2 rectangles
good luck in your class : )
sorry your teacher is not the best!
i am happy that ! could save you!!
could you have taken the second derivative to determine concavity, and therefore whether or not the point is at a max or min?
Thank you so much for these videos! They have helped a bunch :D
Thank you!! This is so simple, and easy to follow. I feel like I understand optimization problems now! :D though probably will have a hard time when I turn to the book haha
Nikolai Hegeman agreed. i literally bought the book only because we're given assignments from it. everything else on it seems really foreign to me
u r still helping us
Thanks for the video.
For this problem we only have one critical problem that was a maximum. If the question were the same but asked for the minimum is it possible to solve? I know you mentioned stretching out the length causing a smaller width but can a specific solution be found to this problem if it asked for minimum dimensions rather than maximum dimensions?
The product of xy is the area of only one rectangle.
So 2xy would be the area of both.
Why did you add the "2x" in the "2x*root*8/3" at the end? did you not already apply the 2x at the start of the question? that's the only part that confused me haha thank you for the video! it's sooooooo helpful! =D
Dylan Holton that is not an x it is supposed to represent "by" as in 2 root 8/3 by 16/3. It was definetely a bit confusing the way he wrote it
nice work, thank you for making it simple.
I have a question. How would you set up the equation(for the constraint) if the question asks for an interval?
Probably not going to pass this part of the test but with what I learned I'm confident I'll get partial credit at least.