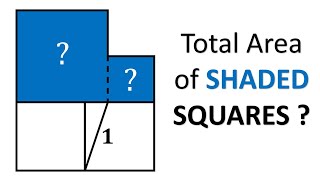
Can you calculate the area of congruent circles inside a right triangle? | An awesome math puzzle
ฝัง
- เผยแพร่เมื่อ 8 ก.พ. 2025
- In this video, we explore a fascinating math puzzle: can you calculate the area of two congruent circles inside a right triangle? This intriguing problem will test your geometry skills and challenge your mathematical thinking! You'll need to apply concepts like congruence, triangle properties, and circle geometry to solve this.
Whether you're preparing for a math competition or just love solving tricky puzzles, this problem is sure to keep your mind sharp. Watch the full explanation, step-by-step solutions, and discover the elegant math behind this geometric wonder!
🔔 Don't forget to like, subscribe, and hit the notification bell for more exciting math puzzles!
Join the Chanel 👉 / @thephantomofthemath
-------------------------------------------------------------------
📧 Contact Me:
✉️ thephantomofthemath@gmail.com
------------------------------------------------------------------
Free Music for Videos 👉 Music by Helkimer - original - thmatc.co/?l=2...








½(12r)+½(9*3r)+½(15r)=54
12r+27r+15r=108
r=2
Area=2(πr²)
Area=2(4π)
Area=8π
A great method.
@@devondevon4366 Thanks! ❤️
Easy. 54= the area of Triangle. So 54=15×r/2+3r^2+r(12-3r)/2+3r(9-r)/2===>r=2
So 54=15*r/2+12*r/2 + 9*3r/2
Wow!
@@lucdery6836 Glad you like it!
CB = a + b + c = 15
a = (5/4)(2r) ; b = (3/4)(12 - 2r) - r ; c = 12 - 3r
Hypothenuse of triangle = √(12² + 9²) = √225 = 15.
On the bottom: 3r + x = 12, with x = the tangent to the right circle from lower right vertex of the triangle, which also shows up on the hypothenuse. Consider the right angled triangle "midpoint of right circle-upper vertex of 9-12-15 triangle-Point(15-x) on hypothenuse", one gets (3r)² + (9 - r)² = (15 - x)² + r²
9r² + 81 - 18r + r² = 225 - 30x + x² + r² | putting x = 12 - 3r
9r² + 81 - 18r + r² = 225 - 30(12 - 3r) + 144 - 72r + 9r² + r²
81 - 18r + r² = 225 - 360 + 90r + 144 - 72r
72 = 36r
=> r = 2. Area = 2·2²·π = 8π sq. units.
Really appreciate your reminders of pertinent theorems as you solved the problem. I saw a 3-4-5 triangle and used trig to get r but I really like your purely geometric approach.
using trigonometry, one gets
12=2r+r+(5/3)r+(4/3)r
leading to r=2
genius solution, without using a calculator
Nice. Solução genial, sem uso de calculadora.👏👏👏
@@luiscostacarlos Thank you! ❤️
I used trig:
Angle ABC= arctan(9/12)
=36.87
Draw a line PB.
Since Triangle QPB=EPB,
angle PBQ=½ ABC
=½(36.87)=18.435
Tan(18.435)=r/(12-3r)
⅓=r/(12-3r)
X-Multiply:
3r=12-3r
6r=12
r=2
Area=2•[Pi(2)²]
=8•Pi
You beat me to it! Alternatively, you can use the tangent double angle formula to determine that tan(
Great job!!!
I solved this ( more like i guessed this) by using out of the box thinking, and it's very fast
we know there's two small circle and we know these two circle don't end up fitting the entire triangle,
assuming the leftover area doesn't end up leaving a room for another circle (that can be cut up and made to fit inside the triangle), we can use these inequality by comparing the two areas
2*pi*r^2 < (9*12)/2
r^2 < 27/pi
r < sq(27/pi) => 2,9316
the nearest integer of this inequality is 2, so we get r = 2
which mean :
Total Area = 2*pi*2^2 = 8*pi
Yes but there can he another method.find the hypotaneous . Area = 1/2 bh for larger triangle. Draw a tangent that divides the triangle into two halves . This tangent is equal to the diameter of two circles. Find the oenth of tangent . With we fan know the radius. Combined area = πr^r + πr^2 = 2πr^2.
The long side of the equation has equation y = 9-3x/4. the circumference of the right hand circle has (y-r)^2 + (x-3r)^2 = r^2. It is straightforward to determine r from these equaqtions and the area of the circles follows easily.
tan α = 9/12 --> α = 36,97°
tan ½α = r / (12-3r) = 1/3
12/r - 3 = 3
r = 2 cm
A = 2 (πr²) = 8π cm² ( Solved √ )
In an algebra class depending on the instructor, using trig may get you marked partial credit, even with the right answer a sound methodology LOL 💯
@@UAPch
Thanks four your comment.
I didn't understand that of "partial credit".
I didn't know that there were credits.
Using trigonometry, all is easier !!!
This videos are not just for students, are for everyone, that says the goal statement of this channel !!
I just solve these exercises, for fun
Nice vdo sir
Thank you sir!
drop a perpendicular to BC from P, PD. PDB and POB triangles are congrunet. If b^ = 2x tan 2x = 3/4. PBD = tan x. OB is 12 - 3r
Using tan formula, 3/4 = 2 tan x / 1 - tan^2 x -> 3tan^2 x + 8 tan x - 3 = 0, tan x = 1/3 or -3
since x > 0, tan x = 1/3
tan x = Po / OB = r/(12- 3r) = 1/3, r = 2
Area = 8pi
I draw a line to each angle A,B and C from center of right circle (point P) and I got 3 triangles
One with the height of r and base of 15
the other with the height of r and base of 12
and the third one with the height of 3r and base of 9
Total of 54r
the area of original triangle 9 × 12,=108 / 2
the sum of 3 triangles area is 54 r over 2
r×54=108
r=2
no calculator needed for this one😏
The radius of inscribed circle in famous 3-4-5 triangle is 1 (not hard to prove). The result follows by reflecting that circle via side length with 3 (in fact we need a picture 2 times proportional to arrive at given 9-12).
Crafty I like it
Thanks. Glad you liked it!
The area of each circle is 4pi, and the area of both circles = is 8pi or 25. 133 Answer
Draw a perpendicular line through the two red circles to form another right triangle 3-4-5 and a trapezoid.
This triangle will be similar to the 9, 12, and 15 triangles above or the 3-4-5 scaled up by 3 since both are right triangles
and share another angle
The new triangle's horizontal base will = 12 - 2r since it is a diameter away ( 2 radii = 1 diameter) from the new triangle
Hence, its vertical base will = 3/4 ( 12- 2r ) = 9 - 1.5 r (Recall, the original triangle is a scaled-up 3-4-5; hence the vertical
side will equal 3/4 of the horizontal side)
Hence its hypotenuse of the vertical side= 5/3 (9 - 1.5 r ) = 15 - 2.5 r HYPOTENUSE
But, according to the tangent circle theorem, the hypotenuse of a triangle ( focus on the new triangle ) when a circle is inscribed
can be determined by the sum of the distance from the point of tangency from both the vertical and horizontal base
Hence, the hypotenuse = (12- 2r - r ) + ( 9-1.5 r - r) = 21-5.5 r
So, the hypotenuse in terms of r is not only 15- 2.5 r but 21-5.5 r
Hence, to find r set both to equal each other 15 - 2.5 r = 21-5.5 r
- 2.5 r + 5.5 r = 21 -15
3 r = 6
r = 6/3
r = 2
The radius of the red circle = 2
Hence, area = pi r^2 = 4 pi
Hence, the area of both circles = 8 pi
@@devondevon4366 Very nice one!
@@ThePhantomoftheMath Thanks. I tried something new, hoping it would work, and it did by forming another 3-4-5 scaled up by 2, hence
6-8-10, and a trapezoid, height 4, bases ( 9 and 6).
Then, I checked if both = the area of the original triangle's area of 54, and it did as
The area of the original triangle (54) is equal to the area of the trapezoid (30) and the area of the 6-8-10 triangle (24).
@@devondevon4366 That's really clever!
@@ThePhantomoftheMath Thanks
I bisected the angle at B to get the two congruent right triangles BPQ and BPE that have the radius as one side. And from there on. I won't type it out here because I then went about it more roundabout than what is probably necessary. The crux is to find a relationship between the triangle and a circle center.
That's a really nice approach!
Actually, this problem is most easily solved using the formula for the radius of the in-circle of a right triangle: R = (1/2)( a + b - c )
In this case we have b = 12 - 2R, a = (3/4)b , c = (5/4)b, and we get a linear equation for R. No need to use Pythagorean Theorem.
The angle at x=12 is arctan(0.75) = 36.8699 degrees. If the red circles have radius r, then the center of the rightmost circle is at x = 3*r, y = r. To get to the tangent point of the rightmost circle with the triangle hypotenuse, we need to increase x by r*sin(36.8699) and y by r*cos(36.8699). So for the tangent point
x = (3+sin(36.8699))*r
y = (1+cos(36.8699))*r
This point must also be on the line y = 9 - 0.75*x. So
9 - 0.75*(3+sin(36.8699))*r) = (1+cos(36.8699))*r
[ (1+cos(36.8699)) + 0.75*(3+sin(36.8699)) ]*r = 9
This solves out to r = 2. Therefore, each circle has area 4*pi, so the total is
Area = 8*pi.
Q.E.D.
The equation of the tangent line to the second circle is y=-3x/4+9 and the equation of the perpendicular line through the center of the second circle is y=4x/3-3r. The intersection gives the point (108/25+36r/25, 144/25-27r/25). The distance of this point to (3r,r) is equal to r which lead to the equation 2r^2-13r+18=0. This results in r=2.
Nice approach!
Assume triangle vertices are A, B, C, labeled counterclockwise from right angle. Left circle center is O, right circle center is P, all as in video. (Paused video here)
Let the point of tangency between circle O and AC be S, and the points of tangency between circles O and P and AB be M and N respectively. Let the point of tangency between circle P and BC be V, and the point of tangency between the two circles will be T. Let the radius of the two congruent circles be r.
As AC = 9 = 3(3) and AB = 12 = 4(3), it's clear that ∆ABC is a 3:4:5 Pythagorean triple right triangle and BC = 5(3) = 15.
As NB and BV are tangent to circle P and intersect at B, NB = BV = x. As SA and AM are tangent to circle O and intersect at A, SA = AM. As ∠OSA = ∠AMO = 90° as S and M are points of tangency and OS and OM are radii, and as ∠SAM = 90°, ∠MOS = 90° as well and SAMO is a square.
As the point of tangency between two circles and their centers is always collinear, OP contains point T, so OP = OT + PT = 2r. As PN and OM are both perpendicular to AB and thus parallel to each other, OMNP is a rectangle with a width of 2r (OP, MN) and height of r (OM, PN).
As AB = 12 and AN = r+2r = 3r, then as x = NB, x = 12-3r. VC thus equals 15-(12-3r) = 3+3r.
Draw PV, and extend NP to L on BC. As ∠BVP = ∠LNB = 90° (radius at tangent), and ∠VLP = ∠BLN = ∠BCA (corresponding angles, as NL is parallel to AC), then ∆PVL and ∆LNB are similar to ∆ABC.
On ∆PVL, as PV = r corresponds to the long leg of the 3:4:5 triangle, then VL = 3r/4 and LP = 5r/4.
BL = BV + VL
BL = x + 3r/4 = 12 - 3r +3r/4
BL = 12 - 9r/4
LN = 5r/4 + r = 9r/4
Triangle ∆LNB:
BL/LN = BC/AC
(12-9r/4)/(9r/4) = 15/9 = 5/3
3(12-9r/4) = 5(9r/4)
36 - 27r/4 = 45r/4
72r/4 = 36
18r = 36
r = 36/18 = 2
Combined circle area:
A = πr² + πr² = 2πr²
A = 2π2² = 8π sq units
Very very nice!
Как то это сложно все. 12 - 4r = 2r, r = 2. Все решение.
Для тех, кто не понял (хотя трудно таких представить). Внутренняя общая касательная (она же радикальная ось) отсечет от треугольника подобный ему треугольник, для которого одна из окружностей, - правая, - вписанная. Так как и тот и другой треугольники подобны треугольнику со сторонами 3,4,5, у которого радиус вписанной окружности 1, то стороны отсеченного радикальной осью треугольника можно записать, как 3r, 4r, 5r, а разница между большими катетами равна 2r.
И никаких длинных уравнений. :)
A = 8π in total
I cheated. I used trig.
One only needs to notice that only the right triangle needs to be solved is that which is formed by right triangle PQB.
The acute angle of PQB is simply the 1/2 angle of the CAB acute angle.
so ...
r/(12-3r) = tan(1/2 angle of CAB)
In the example, r = 2. The rest is just using the pi-r-squared formula.
I wonder if there is a way to do this puzzle from pure geometry without Pythagoras? Maybe, using similar to the trig solution I show above. After all, angles and half-angles and their relationships are well defined with respect to the corresponding ratios of the sides of the right triangle no?
@@krwada No, you didn't "cheat". Trig is completely valid way of solving this problem.