Flux Integrals, Multivariable Calculus
ฝัง
- เผยแพร่เมื่อ 8 ก.พ. 2025
- We look at vector surface integrals, aka flux integrals, aka surface integrals of vector fields. We can imagine the surface S as a permeable membrane that allows a fluid or gas, represented by the vector field F, to flow through it. This analogy helps us understand the orientation and direction of fluid flow across the surface.
We start by comparing scalar surface integrals with vector surface integrals, noting the similarities in the process but also highlighting the crucial difference in how we handle the orientation of the surface. For vector surface integrals, it is essential that the surface S has a specified orientation, which is usually provided in the problem statement.
The process involves
(1) parametrizing the surface,
(2) evaluating the vector field along the parametrization,
(3) differentiating the component functions with respect to the parameters, and then
(4) computing the cross product of these derivatives.
Unlike scalar surface integrals, for vector surface integrals, the orientation of the cross product vector matters significantly as it determines the direction of the normal vector relative to the surface.
So I include a discussion on the concept of orientability, using illustrated examples to show how to analyze the orientation of a given surface. We want to only work with orientable surfaces for the computation of flux integrals, where we can make a consistent choice for the direction of the normal vector.
(Unit 6 Lecture 14)
#calculus #multivariablecalculus #mathematics #integration #flux #iitjammathematics #calculus3 #surfaceintegral #mathtutorial
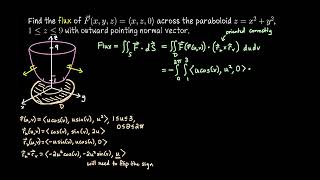







you do NOT UNDERSTAND HOW VIDEOS LIKE THESE actually change LIVES. I'm out here STRESSING OVER MY EXAM and I been looking for ONE VIDEO that CLEARLY EXPLAINS STEP BY STEP. ION GOT TIME FOR ALL THIS EXTRA STUFF. I FINALLY FOUND A VIDEO that CLEARLY, EXPLAINS EVERY SINGLE STEPS. breaks a DIFFICULT PROBLEM INTO STEPS. MAN IM SO HAPPY. GOD BLESS AMERICA for having teachers like you
Meanwhile, comments like this really make MY day! Thank you so much and I'm glad it was helpful.
idk if any1 ever told you this. but you are the goat. im just bummed out that I didn't find this earlier. I hope you make Physics electricity and mag views soon. You have a talent of making complicated stuff pretty simple.
Thank you so much! I'm unlikely to make many physics videos (in the foreseeable future) beyond how it arises naturally in the mathematics that I teach, but I appreciate the encouragement :).
This is probably one of the best videos I've found on TH-cam!
Great explanation!
What a nice thing to say, thank you!
Thank you so much for your video! This is so helpful and it literally saves my life for my upcoming vector calculus test tomorrow!
Great, I hope the test goes well!
@@bevinmaultsby I think I did well today on the test! Thanks!
Awesome!
Are the values on the axises on the graph at 12:22 the correct ones for this unit sphere? Surely not right?
No, good catch. That's a random upper hemisphere I used to sketch the normal vectors on, looks like it was radius 4 rather than radius 1.
At ex.1, how u parameterize?,, the surface is hemisphere right? So shall we use spherical coordinate to parameterize it
Good question. Because it's an upper hemisphere, you have three options here: 1) Rectangular coordinates r(u,v) = (u, v, sqrt(1-u^2-v^2)), 2) Polar coordinates r(u,v) = (ucos(v), usin(v), sqrt(1-u^2)), or 3) Spherical coordinates r(u,v) = (cos(u)sin(v), sin(u)sin(v), cos(v)). I choose option 2, but you can try with the others!
@bevinmaultsby here is why u get my subscribe, thanks in advance from Ethiopia, Mrs,could you recommend me the best book for vector analysis