Find the Flux of the Vector Field F = x i + y j + z^4 k Through the Cone with Downward Orientation

Find the Flux of the Vector Field F = x i + y j + z^4 k Through the Cone z = sqrt(x^2+y^2) beneath the plane z = 1 with Downward Orientation.
Here we first parameterize the cone. A standard parameterization for a cone or a paraboloid or anything with circle symmetry is some variation of x=rcos(t) and y = rsin(t) and z then is determined by the surface equation.
Once we have the parameterization we find the potential normal vector of the surface.
We then check to see if that vector points the way we want it to point by plugging in values of the parameters (this step requires us to fully understand our parameterization)
Once we have the correct normal vector we compute F(s(u,v)) and dot product that with our normal vector.
Lastly we integrate the dot product.

[@MatthewYung-x4b]

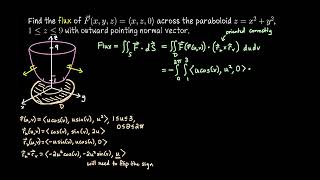
do we use r dr dtheta here at the end of the intergral?

[@mollyabramson]

what if the cone were a function of x and z? would the outward orientation still be in the negative y direction?

[@foreverinhandstand9456]

Great video, thanks! What happens if part of cone is z = 5(x^2 + y^2)^0.5.. does a constant in front change anything?

[@JonathanWaltersDrDub]

That’s becomes z=5r since x^2+y^2 = r^2

[@JakeTheCake254]

When converting to polar coordinates, how come you did not have to multiply by r?

[@JonathanWaltersDrDub]

That's a great question! The jacobian (s_r x s_theta) is the extra multiplier actually. So if we had not use polar coordinates to start and kept our parameterization in terms of x and y then we would have had a double integral in terms of x and y.
Then when switching we would have had to multiply by r. However by setting up our parameterization in terms of r and theta, the cross product automatically produces the r we need. (The cross product is basically the jacobian of the transformation/parameterization, and when we have a change of variables in a double integral that extra r is just the jacobian of polar coordinates.)

[@JakeTheCake254]

@@JonathanWaltersDrDub Wow, thank you that clears up a lot of things!

[@kajavikas7881]

r(dr) (dtheta) is the magnitude of area then while u calculate unit normal for surface area then u get a root 2 at the bottom why did you not considered it

[@JonathanWaltersDrDub]

so. vec{n} = (vec{s}_r x vec{s}_theta)/| vec{s}_r x vec{s}_theta| and d vec{S} = vec{n} dS
and dS = |vec{s}_r x vec{s}_theta| dr dtheta
Thus, vec{F} dot d vec{S} = vec{F} dot vec{n} dS =( vec{s}_r x vec{s}_theta)/| vec{s}_r x vec{s}_theta| dS = (vec{s}_r x vec{s}_theta)/| vec{s}_r x vec{s}_theta| |vec{s}_r x vec{s}_theta| dr dtheta = ( vec{s}_r x vec{s}_theta) dr dtheta.
So the magnitude cancels every time when doing flux.

[@farahasyiqa2652]

hi, may i know when do we use r(theta) x r(r) instead of r(r) x r(theta) because i am confused with that

[@JonathanWaltersDrDub]

The cross product creates a normal vector to the surface. The surface orientation is given in the problem. Your cross product needs to go in the same direction as the orientation of the surface.
For example if the vector is oriented up then the z component of the cross product should be positive no matter what r and theta values you plug into the cross product.
Hope this helps!

[@MusaYmc]

thanks a lot

[@JonathanWaltersDrDub]

You’re welcome! Thanks for watching!

[@wren_g24]

what if upwards orientation? what would change

[@JonathanWaltersDrDub]

The orientation always determines the direction the normal vector points. If it were upward orientation we would want to check to make sure our normal vector always had a positive z component.

[@wren_g24]

@@JonathanWaltersDrDub Thank you so much

[@JonathanWaltersDrDub]

You’re welcome!

[@Oscar_Doggy]

what to change
if z=2?

[@JonathanWaltersDrDub]

Your upper bound for r would be 2. =)

[@sakki3378]

@@JonathanWaltersDrDub what if it just says that z > 0? integrate from 0 to infinity?

[@JonathanWaltersDrDub]

@@sakki3378 Then 0 < r < infinity for the bounds for r in the integral. You'll have to be careful with the integral to infinity because it will be improper and you will need to use the limits to evaluate it.