วีดีโอ

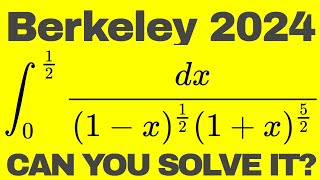
What if a was negative?

Wow, i like how it simplifies though the du initially looked daunting 👍

S=Li_-2(1/2)+2Li_-1(1/2)+3Li_0(1/2)+4Li_1(1/2) Li_1(x)=-ln(1-x) Li_s-1(x)=x•d/dx(Li_s(x)) Li_0(x)=x/(1-x) Li_-1(x)=x/(1-x)^2 Li_-2(x)=x(1+x)/(1-x)^3 S=(3/4)/(1/8)+1/(1/4)+(3/2)/(1/2)-4ln(1/2) S=6+4+3+4ln(2) S=13+4ln(2)

it might not be the fastest method, but it's still my favourite because it lets us solve the general case for sin(x)^n / x^n

Excellent! Yes, it's hard to find examples where it works... But when it does it's very refreshing🍻

sin(ln(x))=(x^i-x^-i)/2i I=-i/2•int(x^(2+i)-x^(2-i))dx I=x^(3+i)/2i(3+i)-x^(3-i)/2i(3-i)+C 1/(3+i)=(3-i)/10 I=x^3/20i•((3-i)x^i-(3+i)x^-i)+C =x^3/10•(3sin(ln(x))-cos(ln(x)))+C

Nice! You can use this approach to easily get the general formula Int[ x^n sin(ln x) = x^(n+1)/( (n+1)^2 + 1) { (n+1) sin(ln x) - cos(ln x)}.

Awesome solution from Waarschijn and excellent presentation!

Nice, thanks!

Very elegant👏👏👏

x=sinθ,I=int(1/(1+sinθ)^2)..θ=0,π/6...

Fantastic

I=int[0,1/2](1/sqrt(1-x^2)(1+x)^2)dx x=sin(t) dt=dx/sqrt(1-x^2) I=int[0,pi/6](1/(1+sin(t))^2)dt t->pi/2-t I=int[pi/3,pi/2](1/(1+cos(t))^2)dt u=t/2 dt=2du I=1/4•int[pi/6,pi/4](sec^4(u))du b=tan(u) db=sec^2(u)du I=1/4•int[1/sqrt(3),1](1+b^2)db I=(b/4+b^3/12)|[1/sqrt(3),1] I=(18-5sqrt(3))/54

Is the other method x = (1-u)/(1+u) ? This is another overpowered secret weapon like the Weierstrass substitution and it works very nicely on this one

Way to stick with it! If instead of updating the bounds with each substitution, you back substituted instead, the integral is a little nicer. It's just -(x+2) sqrt(1-x^2) / 3(x+1)^2, that's the antiderivative of the original without thinking about bounds. Plugging 0 and 1/2 into there is not so bad (at least given how the final answer is, you still have to play with some sqrt(3) in places)

You did a great job! That was pretty unwieldy. It will be interesting to see how the other method compares.

Excellent and clear video👏👏👏A lot of work... You should get some rest... 😀

Now, This is fantastic.❤👏🏽 I did it haphazardly by assuming that n is an integer then the xfloor(x) will now be x² integrating and working out the limit gives 1/3 I think I should invest time and learn how to integrate floor and ceiling functions. Thanks for the video.

Very bad handwriting. Can't read '+' sign properly

The max function in the integrand was very confusing because one may not realize if it's intended to maximize the argument on the variable x or the positive integer k. Based on your clear explanation, x should be considered fixed and k variable in the computation of the max. Essentially what value k should take in order for the max argument to be maximized for a given x.

I don't know if you can actually do this but I got the same answer by seeing it as a limit of the the integral divided by n^3. Then noting that when n->inf both the denominator and numerator tends towards infinity so I can use L'hopitals rule and the numerator simply becomes n*floor(n) by fundemental theorem of calculus. Therefore I=lim n->inf (1/3*floor(n)/n) which I evaluated to be just 1/3👍

Maybe it's because I don't know enough about infinite limits, but shouldn't the summation be from 1 to floor(n), giving a residue integral from floor(n) to n? This made my answer diverge, because it goes to 0 for all non-integer values of n and goes to 1/3 for all integer values of n, which makes more sense to me, since at everywhere except the integer values, n^3 will be much larger that floor(n)^3. So I guess I just want to know why we are allowed to sum directly to n instead of summing to floor(n). Correction: Just did the limit to infinity of ((floor(n))^3)/(n^3) by splitting (floor(n)) into (n-c)^3 for some 0≤c<1, and the limit converges to 1, so my intuition was wrong, and the limitt doesn't depend on whether n is an integer. Going through the math again, this does mean that the integral converges to 1/3 for all values of n. However, it would still be nice to know why we are allowed to sum up to n directly, and not just up to floor(n).

Nice video 👍 actually you can get 1/3 just by getting the highest-degree term at 4:55 (which is (1/3)n^3) and easily get the limit =1/3. on the actual competition this can save a lot of time.

I got the samd answer even tho i made a mistake while taking the integral i forgot about the x so i just put the bounds as theyre😭

This is analogous to Abel's summation formula. Consider the sum 1/2 * \sum_{k\leq n} k^2 = n^3/2 - \int_1^n x[x] dx by the summation formula. Rearrange for the integral, divide by n^2 and apply the formula for a sum of squares. The lower bound of the integral can be 0 or 1 because of the floor function. Taking the limit as n tends to infinity we get 1/2-1/6 = 1/3.

shouldn't the upper bound of the sum be n-1?

Nice job ; )

I am actually quite novice when non-elementary integrals come into place. So could you please explain these integral separately? How did they come into existence and how and why do we write in a way we do? For example, dilogarithm, Si(x) etc. Thanks for such a wonderful video. Happy New Year (I know I'm late 😅) That's all for now. Stay safe and healthy. Have a good day 😊😊

Our beautiful dilogarithm 👏👏👏

I actually was just thinking about this kind of problem with same bounds substitution but for a different integral. Though I am unqualified to give a statement, my opinion is that when we can make a "complete" substitution than there should be no problem, and by "complete" I mean a substitution that doesn't result in +-f(x) in the integrand For example integrating from -3 to 3 over x^2 and setting u = x^2 -> du =2xdx = +-2sqrt(u)dx. Thus the integral stops making sense as we are already integrating over a curve and not a function which is plainly not permitted (at least in single variable calculus)

I was thinking about the following points: Cos(x) =-cos(pi+x) so splitting the integral from o to pi of cos(x) and from pi to 2pi of -cos(pi+x) we can do a substitution for second integral to have y=pi+x so the boundaries become 2 pi to 3 pi but because of periodicity it is just the negative of the first integral so it is a fancy way of writing 0 because of the odd power exponent

Great parametrization. I thought the Feynman's trick carried out twice in the earlier evaluation was awesome, but then this turned out to be even better. Thanks to Samir and you for this excellent evaluation. Have a great 2025 ahead and continue to regale us with these lovely integrals. My question is did the UK Bee guys imagine that Frullani's integrals could pop up here? They are so enamored with the Feynman's trick.

Great insights from Samir, and excellent presentation. This channel brings some of my very distant math memories back alive, excitng and rejuvenating the brain cells in the process. Please keep up the good work.

Awesome 👍

I really enjoyed seeing the alternate use of Feynman's trick. Nice job.

Excellent video👏👏👏 I've never encountered Frullani's Formula... Thanks for the education and Happy 2025🍻

Nice, I liked the slightly more general method shown in the book where we look at a general function d(x) instead of e^(1/x). The property d(x)d(-x)=1 makes the result obvious for any such kind of function d(x)

do you know if the integral of 0 to infinity of e^-(x+1/x)^2 is possible, or have you done a vid on it ?

Worst video. Very bad handwriting. Goes very fast

Fantastic

Where do you find these integrals? I sat the UK int bee 2024 this wasn't on it or is it a different competition?

Or, you can just use the Gamma Function. I=lim(s to 0) int_(0 to inf) e^(-x)*x^(s-2)*(3x-1+e^(-3x))dx, int_(0 to inf) e^(-x)*x^(s-2)*3x dx= 3*Gamma(s), int_(0 to inf) e^(-x)*x^(s-2)dx=Gamma(s)/(s-1), int_(0 to inf) e^(-x)*x^(s-2)*e^(-3x) dx= 4^(1-s)*Gamma(s)/(s-1), so I=lim(s to 0) (3+1/(1-s)-4^(1-s)/(1-s))*Gamma(s), when s approachs to 0, Gamma(s)=1/s, 1/(1-s)=1+s, 4^(1-s)/(1-s)=4+4*(1-ln4)s, so I=4ln4-3. You can also use the same method to solve the other integral you mentioned.

Perfecto👏👏👏 Loved the didactic step-by-step approach🍻

Interestingly enough...you could also use feynman's technique by letting I (t) = the integral given but with e^(-xt) replacing e^(-x)( where t>0).....then by differentiating twice and integrating twice and letting t =1 we get the answer 4ln4 -3 = ln 256 -3

Cool. You could also namnyeF it by noting that the target integral is - d/da Int[ e^(-a x)].

u=e^x du/u=dx I=int[1,2](ln(u)/u^3)du U=ln(u) dv=du/u^3 dU=du/u v=-1/2u^2 I=-ln(2)/8+1/2•int[1,2](u^-3)du I=-ln(2)/8+3/16

Excellent👏👏👏 Almost what I meant... Will send a slightly modified version by email 🍻

Excellent

Unit step function feels like Dirac delta function?

i still can't even begin to comprehend how some people think of these solitons