A Very Nice Math Olympiad Problem | Can You Solve for x? | Algebra
ฝัง
- เผยแพร่เมื่อ 9 ต.ค. 2024
- In this video, I'll be showing you step by step on how to solve this Olympiad Maths Algebra problem using a simple trick.
Please feel free to share your ideas in the comment section.
And if you are new here and you enjoy my content, please hit the like button and subscribe to my channel. Don't forget to hit the bell icon as well so you don't miss on my upcoming videos.


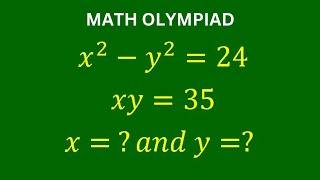






It’s super 👌🏿
Excellent thank you
You're welcome 😊
Thank you for explaining. I will show my method.
Letting, f(x)=(x^2-2)^2, g(x)=x+2, f(2)=g(2)=2 and f(-1)=g(-1)=1. Therefore, f(x)-g(x) is divided by (x-2)(x+1) [=x^2-x-2].
>
∴ x^4 - 4x^2 - x + 2 = (x^2-x-2)(x^2+ax+b) ∴ x^2+ax+b = x^2 + x - 1 From x^2+x-1=0, x=(-1±√5)/2 ∴ x = 2, -1, (-1±√5)/2
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
I guess the test-maker respected the test-takers can calculate or find x=-1,2 at the beginning when he/she made this problem.
Judging from the left side of the given equation is (・・・)^2, if x has integer solutions, the value of (x^2-2)^2 [=x+2] is 0, 1, 4, 9, ・・・.
The case of =0 should be rejected because x^2-2 cannot be 0 if x is an integer. And, we can find x=-1 and x=2 easily by trial and error.
Thus, we can get 2 integer solutions at the beginning without complicated calculation.
・・・ Hence, I guess the test-maker made the problem because he/she tried to know the test-takers' can notice the calculation that I typed above.
Simpler method: Once you get the equation at 2:42 you can use the Rational Roots Theorem and see immediately that the only possible rational roots are 1,-1,2 or -2. Testing these options and finding x_1 and x_2 only takes a few seconds. Then you can divide by (x+1)(x-2) and get the second degree equation that gives you x_3 and x_4.
Nice problem
other solution are
Method 1
(x^-2)^2 = x+2
Let y= x^ 2 - 2
then y^2 = x+2
adding these equations
x^2+x =y^2+y
(x-y)(x+y+1) = 0
(x-x^2+2)(x+x^2-2+1) = 0
(x^2-x-2)(x^2+x-1) = 0
(x+1) (x-2) (x^2+x-1)=0
Method 2
subtracting x^2 both sides and factorising LHS
(x^2-2+x ) ( x^2-2-x) = x+2-x^2
transposing RHS to LHS and taking common
(x^2-x-2)(x^2+x-1) = 0
Method 3
x4-4x^2-x+2 = 0
suppose that factorisation of expression is
(x^2+px+a )(x^2-px+b) then
a+b-p^2= - 4
P (b-a ) = - 1
ab = 2
Now (a + b)^2 - (a - b)^2 = 4ab hence
(P^2-4)^2 -1/p^2 = 8 let t = p^2
t^2-8t+16-1/t = 8
t^3-8t ^2+16t-9 = 0
t = 1 because sum of coefficients is zero
hence p = 1
a+b = -3 , a - b = 1
hence a = -1 , b = -2
(x^2+x-1)(x^2-x-2) = 0
Method 4
let a = 2 then
x^4+a^2-2ax^2-x-a = 0
a^2 - (2x^2+1)a + (x^4-x)= 0
Discriminant is
4x^4+4x^2+1-4x^4+4x = (2x+1)^2
a =(2x^2+1+2x+1)/2 , (2x^2+1-2x-1)/2
hence 2 = x^2+x+1 and x^2-x
x^2+x-1 =0 , x^2-x-2 = 0
Superb! 👌
(x² - 2)² = x + 2
x⁴ - 4x² + 4 = x + 2
x⁴ - 4x² + 4 - x - 2 = 0
x⁴ - 4x² - x + 2 = 0 ← it would be interesting to have 2 squares on the left side (because power 4 and power 2)
Let's rewrite the equation by introducing a variable "λ" which, if carefully chosen, will produce 2 squares on the left side
Let's tinker a bit with 25x⁴ as the beginning of a square: x⁴ = (x² + λ)² - 2λx² - λ²
x⁴ - 4x² - x + 2 = 0 → where: x⁴ = (x² + λ)² - 2λx² - λ²
(x² + λ)² - 2λx² - λ² - 4x² - x + 2 = 0
(x² + λ)² - [2λx² + λ² + 4x² + x - 2] = 0 → let"s try to get a second member as a square
(x² + λ)² - [x².(2λ + 4) + x + (λ² - 2)] = 0 → a square into […] means that Δ = 0 → let"s calculate Δ
Δ = (1)² - 4.[(2λ + 4).(λ² - 2)] → then, Δ = 0
(1)² - 4.[(2λ + 4).(λ² - 2)] = 0
4.[(2λ + 4).(λ² - 2)] = 1
8.[(λ + 2).(λ² - 2)] = 1
(λ + 2).(λ² - 2) = 1/8
λ³ - 2λ + 2λ² - 4 - (1/8) = 0
λ³ + 2λ² - 2λ - (33/8) = 0
λ = - 3/2
Restart
(x² + λ)² - [x².(2λ + 4) + x + (λ² - 2)] = 0 → when λ = - 3/2, a square will appear
[x² - (3/2)]² - [x².(2.{- 3/2} + 4) + x + ({- 3/2}² - 2)] = 0
[x² - (3/2)]² - [x².(- 3 + 4) + x + ({9/4} - 2)] = 0
[x² - (3/2)]² - [x² + x + (1/4)] = 0 ← we can see a square
[x² - (3/2)]² - [x + (1/2)]² = 0 → recall: a² - b² = (a + b).(a - b)
{ [x² - (3/2)] + [x + (1/2)] }.{ [x² - (3/2)] - [x + (1/2)] } = 0
[x² - (3/2) + x + (1/2)].[x² - (3/2) - x - (1/2)] = 0
[x² + x - (2/2)].[x² - x - (4/2)] = 0
(x² + x - 1).(x² - x - 2) = 0
First case: (x² + x - 1) = 0
x² + x - 1 = 0
Δ = (1)² - (4 * - 1) = 5
x = (- 1 ± √5)/2
Second case: (x² - x - 2) = 0
x² - x - 2 = 0
Δ = (- 1)² - (4 * - 2) = 9
x = (1 ± 3)/2
Solution = { (- 1 - √5)/2 ; - 1 ; (- 1 + √5)/2 ; 2 }
Excellent job well done 👏