Japanese Math Olympiad | A Very Nice Geometry Problem | 3 Different Methods

Japanese Math Olympiad | A Very Nice Geometry Problem | 3 Different Methods
MY OTHER CHANNELS
••••••••••••••••••••••••••••••••
Calculus Booster : / @calculusbooster
Math Hunter : / @mathshunter
--------------------------------------------------------------------------------
Join the channel to become a member
/ @mathbooster

[@prime423]

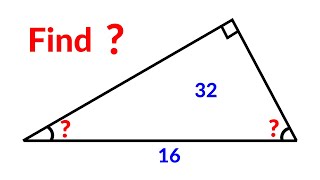
The most important part of the solution is an analysis of the problem. For example, how do we use the given information. The details most solvers know and be glossed over. These problems are teaching moments!!

[@ROCCOANDROXY]

Let theta = angle(BDA) implies angle(B) = 135(degrees) - theta and using law of sines on triangle(ABD) implies sin(theta) = x/(5 * sqrt(2)) implies cos(theta) = sqrt(50 - x^2)/(5 * sqrt(2))
and in triangle(ABC) we have 3/x = sin(135(degrees) - theta) = (sqrt(50 - x^2) + x)/10 implies 30 - x^2 = x * sqrt(50 - x^2) implies (x^2 - 45) * (x^2 - 10) = 0 implies x = sqrt(10), 3 * sqrt(5).
Let DC = j. For x = sqrt(10) implies j^2 + 10 * j + 24 = 0 implies j < 0 implies drop x = sqrt(10). For x = 3 * sqrt(5) implies (j + 11) * (j - 1) = 0 implies j = 1. Therefore x = 3 * sqrt(5).

[@Istaphobic]

I did it the following way:
Extend line AD to point E and construct a line from B to meet line AE such that ∠BEA = 90°
Let ∠CAD = α
⇒ ∠EBC = ∠CAD = α as ∠BEA = ∠DCA = 90° as BECA is a cyclic quadrilateral (Butterfly Theorem). So ∠EBC = α
∴ △BDE ~ △ACD (angle-angle-angle)
Now, as ∠CAB = 45 + α, ⇒ ∠ABC = 45 - α (angles of a triangle add up to 180°), however, as ∠EBC = α, ∴ ∠EBC + ∠ABC = 45 - α + α = 45°
∴ △ABE is a 90°-45°-45° isosceles triangle, and as ∠ABE = ∠BAE = 45° ⇒ BE = AE
As line AB = 𝑥, ∴ BE = AE = 𝑥/√2 (Pythagoras' Theorem)
Now, letting line AD = y, and as △BDE ~ △ACD, ∴ (𝑥/√2)/5 = 3/y
⇒ y = 15√2/𝑥
Taking △BDE, (𝑥/√2 - 15√2/𝑥)² + (𝑥/√2)² = 5² (Pythagoras' Theorem)
⇒ 𝑥²/2 - 30 + 450/𝑥² + 𝑥²/2 = 25
⇒ 𝑥² + 450/𝑥² - 55 = 0
⇒ 𝑥⁴ - 55𝑥² + 450 = 0
⇒ (𝑥² - 10)(𝑥² - 45) = 0
⇒ 𝑥² = 10 or 45
⇒ 𝑥 = ±√10 or ±√45
Now, 𝑥 > 5 as line BC > 5 (hypotenuse > either side of a right-angled triangle)
And √10 < 5
⇒ 𝑥 = √45
∴ 𝑥 = 3√5

[@MarieAnne.]

My method started off the same as method 3 in video:
Let θ = ∠CAD, and let CD = a
tan θ = a/3 and tan(θ+45) = (a+5)/3
Now we calculate a using the tangent formula for difference of angles:
tan((θ+45)−θ) = tan 45
(tan(θ+45) − tan θ) / (1 + tan(θ+45) tan θ) = 1
((a+5)/3 − a/3) / (1 + ((a+5)/3)(a/3)) = 1
(5/3) / ((9 + (a+5)a)/9) = 1
15 / (9 + a² + 5a) = 1
a² + 5a + 9 = 15
a² + 5a − 6 = 0
(a − 1) (a + 6) = 0
Since a is a length, then a > 0
a = 1
Using Pythagorean Theorem in △ABC, we get:
x² = 3² + (5+1)² = 9 + 36
x² = 45
*x = 3√5*

[@jimlocke9320]

In the third method, the notation made be made easier to work with by designating length CD as a, as you did in the first 2 methods. Then, tan(Θ) = a/3 and tan(Θ + 45°) = (a + 5)/3. Apply the tangent sum of angles formula tan(α + ß) = (tan(α) = tan(ß))/(1 - tan(α)tan(ß)) where tan(α) = tan(Θ) = a/3, tan(ß) = tan(45°) = 1 and tan(α + ß) = tan(Θ + 45°) = (a + 5)/3. So, (a + 5)/3 = ((a/3) + 1)/(1 - (a/3)(1)). The positive solution is a = 1. Alternatively, let tan(Θ) = b and then CD = 3b, which also simplifies the notation in your equations.

[@User-jr7vf]

There's yet a fourth method, which is what I used before watching the solution, which consists of using the Law of Sines in the triangles ABC and ADC to express length AD in terms of x only, then using the Law of Cosines in the triangle ABD to solve for x.

[@jonpress6773]

Here's another, similar but different: Let Θ =

[@hungtran-zs4tx]

DAC= x ; AD=3/cosx ;
AD=(BD/sin45)XsinABC=5/(cosx-sinx); from that we have an equation: 3/sinx=5/(cosx-sinx) and then equation changed to: 3tanx^2+5tanx-2=0 and root tanx=1/3 ; DC=3tanx=1; X^2=AC^2+BC^2=3^2+6^2=45 and then X=3√5 .

[@Irtsak]

*If you have n variables, you usually need n equations*
The easiest thing is to discover them with the help of the scheme.
The most difficult thing is to solve the system, since the equations are independent !!!!
Let DE⊥AB and AE=α => BE=x-α
Triangle AED is obviously isosceles => AE=ED=α . Very easily AD=a√2
Using areas :
(ABD+(ADC) = (ABC) => 1/2⋅ αx+1/2⋅ 3y=1/2⋅ 3(5+y) => *αx=15* (1)
Pythagoras in triangle BED => (x-α)²+α²=5² => x²+2α²-2αx=25
=> x²+2α²⋅ 2⋅ 15=25 cause (1)
x²+2²=55 => x²+y²+9=55 => *x²=46-y²* (2)
Pythagoras in triangle ABC => x²=(y+5)²+3² => x²=y²+10y+34
=>46-y²=y²+10y+34 cause (2)
=> y²+5y-6=0 => y=1 (y>0)
So by (2) => x²=45 ⇒ *x=3√5*

[@supriyomondal5139]

Using the figure of method 2, in 📐 BDE b²+(x-b)²=5²=25
&
In 📐 BDE and 📐 ABC respectively
sine of angle B=(x-b)/5 =3/x
Substitute b w.r.t. x and replace b in the first eqn we get an equation of x of fourth power which has 4 solution out of which √45 is the only solution

[@papkenhartunian186]

You could have calculated the tangent of angle DAC = DC/3 and also you could have calculated the tangent of angle BAC = (5+DC)/3. Then use tangent of angles (BAD + DAC) = (Tang BAD + Tan DAC)/(1-tangent BAD. Tangent DAC). Eazyly, you could find the tangent of DAC =1/3 which lead you to the DC and next to get X.

[@michaeldoerr5810]

This is the first time that I thinj that the third method is much much easier. Perhaps I should apply that method to similar geometry problems. What do you think?

[@MathBooster]

Yes, third method is easy. But sometimes geometry problems are not allowed to solve by using trigonometry, so you need to learn first and second method also.

[@mariopopesco]

Angle ABC =@
So, angle ADC = 45+@
In triangle ABD, sin ADC = 3/ AD --> sin (45+@) = 3/AD --> AD = 3 / (sin 45 * cos @ + cos 45 * sin@) --> AD = 3 sqrt(2) / (cos @ + sin @)
In triangle ABD , sines law : AD / sin @ = BD / sin 45 --> AD = 5 sqrt (2) * sin @
So, 5 sqrt (2)* sin @ = 3 sqrt (2) / (sin@ + cos@) -->
(sin @)^2 + sin @* cos @ = 3/5 , and (sin@)^2 + (cos@)^2 = 1 -->
(sin @)^2 + sin @* cos @ = 3/5 * [(sin@)^2 + (cos@)^2], we divide by (cos @)^2 -->
(tan @)^2 + tan @ = 3/5 [(tan @)^2 + 1] , positive solution tan @ = 1/2 -->
In triangle ABC : tan @ = AC / BC --> BC = AC / tan @ = 3 / (1/2) = 6 -->
Pithagora in triangle ABC : X^2 = 3^2 + 6^2 = 45 --> X = 3 sqrt5

[@user-zy1rw6yb9p]

Thanks for watching

[@yakupbuyankara5903]

X=3×(5^(1/2))

[@prossvay8744]

X=3√5

[@comdo777]

asnwer=15 isit

[@User-jr7vf]

Yes, the "asnwer" can be 15 for all we know. However, the answer is not 15.

[@lnmukund6152]

Mr anerobic
Ur process is 2 mch cumbersome, totally un lucid, invalid, sorry
Mukund