A Simple Sequence, with Fun Consequences
ฝัง
- เผยแพร่เมื่อ 4 มิ.ย. 2024
- We define a sequence by taking n starting terms x_1, ..., x_n, then defining each subsequent term as the arithmetic mean of all previous terms. Studying this sequence allows us to uncover some interesting results about partial fractions.
00:00 The Sequence
01:10 Why is this interesting?
02:03 First result
03:52 Second result
07:02 Dealing with the final term
09:21 Conclusion



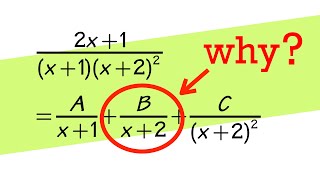



![[UNCUT]"เศรษฐา" โดนบีบให้ลาออก เผยดีลลับ "ทักษิณ" ต้องต่อโปร ไม่งั้นเจอจุดจบ! I คนดังนั่งเคลียร์](http://i.ytimg.com/vi/XlH3k81dxmE/mqdefault.jpg)

a very interesting way to generate partial fraction definitions! great video as always Dr. Barker.
I wonder if there's a way to use this line of thinking to derive identities where the denominator polynomial doesn't factor into consecutive terms?
I can see how we could quite easily generalise the argument at 07:02 to any two non-consecutive terms like n(n + k), using that x_{n+k} = S/n = (S + kS/n)/(n+k).
We should be able to do something similar for three terms like n(n + k)(n + k + a), using a setup along the lines of x_{n+k+a} = S/n = (S + (k+a)S/n)/(n+k+a) = (S + (k+a)(S + kS/n)/(n+k))/(n+k+a), where we use the fact that S/n = (S + kS/n)/(n+k) for the last step.
@@DrBarker very interesting. thanks for the detailed reply!
I follow you from 500 subs you never disappointed
I'm glad you're still watching!
Just found another pearl... Thx!
That's interesting it can be used to simplify raising factorials, I wonder what would the expansion approach for 1/n*(n+1)...(n+k) as k approaches infinity
i imagine youre asking for a generalisation of these expansions, because taking k->inf will just get you 0
WARNING: RANT AHEAD
Not actually gonna use the sequence, just gonna PFD this some other way, sorry
I'm using cover up method btw
S/n = S/n
S/n(n+1) = S/n - S/(n+1)
S/n(n+1)(n+2) = (1/2)S/n - S/(n+1) + (1/2)S/(n+2)
S/n(n+1)(n+2)(n+3) = (1/6)S/n - (1/2)S/(n+1) + (1/2)S/(n+2) - (1/6)S/(n+3)
The coefficients look like this series of numbers
so for S/n(n+1)...(n+k) you might expect the S/(n+j) term to have coefficient (-1)^j / (j!)(k-j)! which is almost the choose function but not quite
I wanna check the other properties of these terms just as terms without the S/(n+j) stuff
k=0:{1}
k=1:{1, -1}
k=2:{1/2, -1, 1/2}
k=3:{1/6, -1/2, 1/2, -1/6}
k=4:{1/24, -1/6, 1/4, -1/6, 1/24}
k=5:{1/120, -1/24, 1/12, -1/12, 1/24, -1/120}
k=6:{1/720, -1/120, 1/48, -1/36, 1/48, -1/120, 1/720}
their product has something to do with hyperfactorials
their sum is always 0. can only prove it for the odds bc that ones easier
half of the terms are the negative of the other half so everything cancels nicely
It's a binomial expansion
S*Πᵢ₌₀ⁱ⁼ᵏ(1/(n+i))=S*∑ᵢ₌₀ⁱ⁼ᵏ((-1)ᵏ/(i!(k-i)!(n+i)))
Although proving it is the challenge. It'd probably have to be by induction.
@@ThAlEdison could do with the cover up method of partial fraction decomposition, no induction needed
The coefficient of S/(n+j) would be:
plug in n = -j into prod[1/(n+i); i = 0 -> k && i ≠ j]
= prod[1/(i-j); i = 0 -> j-1] * prod[1/(i-j); i = j+1 -> k]
= (-1)^j/(j!)(k-j)!
Next thing to prove: they look like the coefficients of pascal's triangle, scaled by 1/k! and also alternating
k!/j!(k-j)! is by definition k choose j
which should appear in pascal's triangle
for the pascal's triangle of the zero property i mentioned earlier i think i have something but it's not rigorous
construct pascal's triangle as follows:
start with 1
each element in the row below is now the element in the upper right MINUS the element in the upper left
which can also be thought of as this operation
to get row R+1, copy row R down to the left, the negate R, copy it down to the right, and add
for example if the row was 1 -3 3 -1
i would have
1 -3 3 -1
-1 3 -3 1
1 -4 6 -4 1
pretty easy to see that starting from row 1 (the tip of the triangle is row 0) all the sums should add up to 0
the base case is that row 1 = 1 -1 which so obviously sums to 0
and since all rows after are just copies of the row above shifted around, it's all 0 - 0 = 0 in the end
+1 -3 +3 -1 = 0
-1 +3 -3 +1 = 0
+1 -4 +6 -4 +1 = 0 + 0 = 0
I found a much simpler proof as follows.: write x[n]= 1/(n-1)*( x[1]+x[2]+ .....x[n-1]) and
x[n+1) = 1/n*(x[1]+x[2]+ ... x[n-1]+ 1/(n-1)*( x[1]+x[2]+ .....+x[n-1]) ).
But the last expression can be written as 1/n*(n-1+1)*1/(n-1)*(x[1]+.....+x[n-1]) . Since 1/n*(n-1+1)/(n-1 ) = 1/(n-1), this means that all terms
after the first given ones are just the same , namely the mean of the first given ones , i.e. they are all equal.
Nice video and catchy title!
next is to take this all the way to S/n!
Why not this much more simple solution:
This definition starts at x2 , that is xn+1 with n=1, 2, ... (n can't be 0 otherwise we'd divide a sum of 0 elements by 0 which can't work)
So x1 is not defined, but x1 is used in the definition, so we need to define it, say x1=k.
then we see that x2 = x1/1 = x1 ( = k ) .
next, x3=(x1+x2)/2 = 2x1/2 = x1.
x4 = (x1 + x2 + x3)/3 = 3x1/3 = x1
etc
=> xn = x1 = k for all n.
This is true but it wasn't the point of the video. It is easy enough to see that each term has to be the same once we define the subsequent term to be an average. The trick here was to derive pfd without having to do the normal algebra calculations using the above sequence
Yes, I think the fact that the sequence is allowed to start with n terms x_1, ..., x_n, is actually redundant, and we could still do the same calculations and derivation of partial fractions results if the sequence just had a single starting value x_1. So we could actually get the same partial fractions results from an even simpler type of sequence!
i found a simpler solution, n has to be greater or equal to 2 since 1-1 =0 and we cant divide a sum of 0 elements, using mathematical induction we can see xn = x1. x2 = x1/1 = x1. we are going to asume xk is true, x(k+1) = (x1+x2+x3+...xk)/(k+1-1) since we assument xk = x1 we will get k(x1)/k = x1 and because this is true we get xn = x1 for any values of n bigger or equal to 2
this just seems like a bunch of random math
PROF UR VIDEOS too ADVANCED.
Then, don’t Watch them
This takes the prize for the least interesting sequence ever. An interesting paradox, too advanced yet not advanced at all.
:-/
Rip bozo