Germany | Can You Solve This | A Nice Math Olympiad Problem | You Should Learn This Best Trick.

In this Math Olympiad problem, we tackle the equation and find the value of with a clear, step-by-step solution. Perfect for math enthusiasts looking for a challenge!
#MathOlympiad #MathChallenge #CubicEquation #Algebra #ProblemSolving #STEM #MathLovers

[@wes9627]

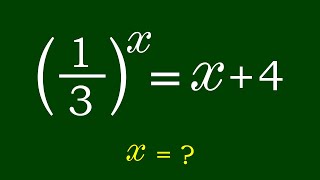
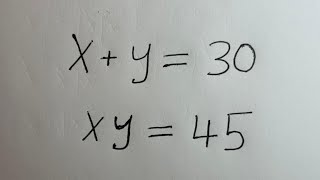
Students, learn this symmetric trick for faster solution. Substitute x=10+z and y=10-z into the second equation: (10+z)(10-z)=200.
z^2=100-200=-100 yields z=±10i, x=10±10i, and y=10∓10i.

[@aldoazcona5383]

X=?
Y=?

[@walterwen2975]

Germany, Math Olympiad: x + y = 20, xy = 200; x,y =?
(x - y)² = (x + y)² - 4xy = 20² - 4(200) = - 400 = (20i)², x - y = ± 20i; x + y = 20
2x = 20 ± 20i, x = 10 ± 10i; 2y = 20 -/+ 20i, y = 10 -/+ 10i
Answer check:
x = 10 ± 10i, y = 10 -/+ 10i: x + y = (10 ± 10i) + (10 -/+ 10i) = 20; Confirmed
xy = (10 ± 10i)(10 -/+ 10i) = 10² - (10i)² = 100 + 100 = 200; Confirmed
Final answer:
x = 10 + 10i, y = 10 - 10i or x = 10 + 10i, y = 10 - 10i

[@aldoazcona5383]

Not solution

[@ORCODEMONE]

x = 10 y = square root 100