Can you find the area of the tiny Red shaded region? | (Semicircle and Triangle) |
ฝัง
- เผยแพร่เมื่อ 9 ก.พ. 2025
- Learn how to find the area of the tiny Red shaded region. Important Geometry and Algebra skills are also explained: Thales' theorem; area of a triangle formula; area of a sector formula; Pythagorean theorem. Step-by-step tutorial by PreMath.com
Today I will teach you tips and tricks to solve the given olympiad math question in a simple and easy way. Learn how to prepare for Math Olympiad fast!
Step-by-step tutorial by PreMath.com
• Can you find the area ...
Need help with solving this Math Olympiad Question? You're in the right place!
I have over 20 years of experience teaching Mathematics at American schools, colleges, and universities. Learn more about me at
/ premath
Can you find the area of the tiny Red shaded region? | (Semicircle and Triangle) | #math #maths
Olympiad Mathematical Question! | Learn Tips how to solve Olympiad Question without hassle and anxiety!
#FindRedArea #Triangle #Sector #AreaOfSector #Radius #AreaOfTriangle #CircleTheorem #GeometryMath #EquilateralTriangle #PythagoreanTheorem #PerpendicularBisectorTheorem #ThalesTheorem
#MathOlympiad #ThalesTheorem #RightTriangle #RightTriangles #CongruentTriangles
#PreMath #PreMath.com #MathOlympics #HowToThinkOutsideTheBox #ThinkOutsideTheBox #HowToThinkOutsideTheBox? #FillInTheBoxes #GeometryMath #Geometry #RightTriangles
#OlympiadMathematicalQuestion #HowToSolveOlympiadQuestion #MathOlympiadQuestion #MathOlympiadQuestions #OlympiadQuestion #Olympiad #AlgebraReview #Algebra #Mathematics #Math #Maths #MathOlympiad #HarvardAdmissionQuestion
#MathOlympiadPreparation #LearntipstosolveOlympiadMathQuestionfast #OlympiadMathematicsCompetition #MathOlympics #CollegeEntranceExam
#blackpenredpen #MathOlympiadTraining #Olympiad Question #GeometrySkills #GeometryFormulas #Angles #Height
#MathematicalOlympiad #OlympiadMathematics #CompetitiveExams #CompetitiveExam
How to solve Olympiad Mathematical Question
How to prepare for Math Olympiad
How to Solve Olympiad Question
How to Solve international math olympiad questions
international math olympiad questions and solutions
international math olympiad questions and answers
olympiad mathematics competition
blackpenredpen
math olympics
olympiad exam
olympiad exam sample papers
math olympiad sample questions
math olympiada
British Math Olympiad
olympics math
olympics mathematics
olympics math activities
olympics math competition
Math Olympiad Training
How to win the International Math Olympiad | Po-Shen Loh and Lex Fridman
Po-Shen Loh and Lex Fridman
Number Theory
There is a ridiculously easy way to solve this Olympiad qualifier problem
This U.S. Olympiad Coach Has a Unique Approach to Math
The Map of Mathematics
mathcounts
math at work
Pre Math
Olympiad Mathematics
Two Methods to Solve System of Exponential of Equations
Olympiad Question
Find Area of the Shaded Triangle in a Rectangle
Geometry
Geometry math
Geometry skills
Right triangles
imo
Competitive Exams
Competitive Exam
Calculate the Radius
Equilateral Triangle
Pythagorean Theorem
Area of a circle
Area of the sector
Right triangles
Radius
Circle
Quarter circle
coolmath
my maths
mathpapa
mymaths
cymath
sumdog
multiplication
ixl math
deltamath
reflex math
math genie
math way
math for fun
Subscribe Now as the ultimate shots of Math doses are on their way to fill your minds with the knowledge and wisdom once again.
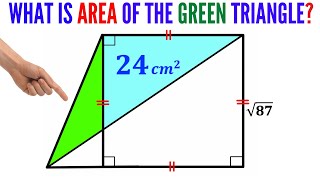







Thales Theorem is a special case of the Inscribed Angle Theorem and that Angle ABE is always 90⁰. Then Sector Area minus Area of Triangle EOD is just iceing on the cake. 🙂
Thanks ❤️🌹
Awesome, the sheer adroitness of your clarification combined with the quality of the video makes for less intricacies and obstacles!
Thanks ❤️🌹
1/Calculating the radius R:: connect EB, we have EBA is a right triangle of which the angle A= 45 degrees EBA is an right isosceles one. So the diameter EA =8sqrt2----> r= 4sqrt2.
2/Calculating the value of angle EOD: notice that the triangle ADC is a special right 30-90-60 triangle-----> angle DAC= 30 degrees --------> angle EAD= 45-30=15 degrees-----> the angle EOD = 30 degrees ( EOD is the angle at the center).
3/Calculating the Area of the sector OED:: = pi sq(4 sqrt2) , 30/360 = pi . 32. 1/12 = 8 pi/3 (1)
4/Calculating the area of the triangle OED: drop the height EH to OD. We have the triangle EHD is a special 30-90-60 too, so EH= EO/2= 2 sqrt2
the area of the triangle EOD= 1/2 . 2sqrt2 .4sqrt2= 8 (2)
5/ Area of the red segment= (1)- (2) = 8pi/3 -8 =
Got it! A very good exercise, many thanks.
Very Very nice video sir 👍
So nice of you
Thanks ❤️🌹
Can you please make some more videos on algebra also
From triangle AEC you can immediately see that angle AEC = 75 = 180 - 69 - 45.
Angle is 75 degrees can be obtained from initial given triangle itself. Also, diameter can be seen to be the hypotenuse of the isosceles triangle and diameter is 8.sqrt(2).
I solved the problem using various geometry and the law of sines, and subsequently solved it using integral calculus. In both cases I reached identical outcomes matching your result.
Nice. Alternatively, angle E=75 and after drawing radius OD we have Isosceles triangle OED which forces central angle EOD=30. To find r, inscribed angle A=45 forces central angle EOB=90 which makes triangle AOB a 45-45-90 right triangle. Hence, r=OA=4√2 so with angle EOD=30 the red area is found like you did.
Trigonometric magic!
Thanks ❤️
8 is equal to a side length of a Square, Hence the diagonal, the Radius turns out to be 8* sqrt 2.
Pretty much the same way I solved it, except that I calculated ∠OED from △ACE:
∠OED = ∠AEC = 180° − ∠ACE − ∠CAE = 180° − 60° − 45° = 75°
I calculated angle OED from triangle ACE.
Also, EA = sq.rt.128, so r = 1/2 x sq.rt 128 = sq.rt.32.
Then sector area = Pi x (sq.rt.32)^2 /12.= Pi x 32 /12 = Pi x 8 /3.
Nice, many thanks, Sir! (8/3)(π - 3)
Very good!
Thanks ❤️🌹
From D we can drop the perpendicular to EO, calling H the point of intersection; we have the 30°-60°-90° triangle HDO, so we can put 2DH= 4square root of 2, so DH= 2square root of 2, then finally the same method you finished the problem putting EDO= EO•DH/2
Thanks
The area of a circular sector is ½ R² θ where R is the radius of the circle and θ the central angle in radians.
The area of the isosceles triangles defined by the same three points as this circular sector is ½ R² sin θ.
Therefore, the area of a circular segment is ½ R² θ − ½ R² sin θ which simplifies to ½ R² (θ − sin θ).
yes, but you didn't find theta or R, so your answer is just incomplete
0.37758 Answer
A different approach
Draw a straight line from B to E, forming an isosceles right triangle ABE.
BE = 8 due to BA= BE ( 45 45 and 90 degrees)
AE = (diameter) 8 sqrt 2 due 45 45 90
Hence, the radius of the circle = 4 sqrt 2
Draw a straight line from O to D . This is the radius.
But O E is also the radius. Hence, triangle EDO is an isosceles with the angles.
75 75 and 30 degrees
length ED of triangle EDO can be derived from the cosine formula
c= sqrt(a^2 + b^2 - 2ab cos 30
a= 4 sqrt 2 , b = 4 sqrt 2 Gamma 30
c = 2.93
The area of triangle EDO can be derived from using Heron's formula
and the sides 2.93, 4 sqrt 2, and 4 sqrt 2
Area of of EDO = 8
Since the area of EDO + the small red-shaded region equal
1/12 of the circle (since the circle covers 360 degrees and 360/30 =12),
then the area of EDO + the red segment = 1/12 area of the circle
The area of the full circle = 4 sqrt 2 pi r^2 = 100.53 square units
Hence the are of EDO + the small red segment = 100.53096/12 or 8.37758
Since the area of EDO (as calculated earlier) = 8
then the area of the red segment = 8.37758 - 8 = 0.37758
Area of the red shaded region=π(4√2)^2(30/360)-1/2(4√2)^2sin(30)=8π/3-8=0.38 square units. Thanks ❤❤
Thanks ❤️🌹
The AEC=75°=180°-60°-45°....
It is only a half