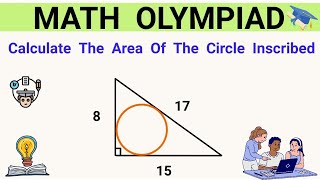
How to find side length of a square inside a triangle | Area of square inside a triangle

How to find side length of a square inside a triangle | Area of square inside a triangle
area of a triangle
triangle
find side of square inside a triangle
area of square inside a triangle
square of max. area inside a triangle
perimeter of square inside a triangle
square
right triangle
square inside in a triangle
area of triangle
square inside a triangle theorem
square inside a triangle
how to find the area of a triangle
how to find the area of a triangle step by step
how to do area of triangle
find the area of a triangle step by step
Join this channel to get access to perks:
/ @mathbooster
MEMBERS OF THIS CHANNEL
••••••••••••••••••••••••••••••••••••••••
Mr. Gnome
ஆத்தங்கரை சண்முகம்
Εκπαιδευτήρια Καντά
堤修一
Sidnei Medeiros Vicente
Sambasivam Sathyamoorthy
Muhtar Samedov
Gerard van Bemmel
Petr'ahcz
Khusi Wala
Gopal Yadav
Sam
Fatih Ekşioğlu

[@RobG1729]

A recent video on another channel used that ( a = bh/b + h ) without demonstrating that property of a square within a triangle as you've done so well here.
Thanks so much

[@AAZ3000]

Theorems are used the same way. Once proved and shown, they are applied in geometry problems without proving them again

[@dimuthdarshaka7985]

Sir I did this way triangle
ABC Area - ARS Area - BPS Area - QCR Area = a^2
Triangle BPS and QCR base is equal to (10-a) .
Thanks

[@marioalb9726]

Similarity of triangles:
(h-a)/a = h/b = 8/10
h/a - 1 = h/b
h/a = h/b +1
a = h / (h/b+1)
a = 8 / (8/10+1) = 80/18
a = 40/9 cm

[@marioalb9726]

Similarity of triangles:
(h-a)/a = h/b. = 8/10
(h-a) = 4/5 a
a + (h-a) = h
a + 4/5 a = 8
9/5 a = 8
a = 40/9 cm ( Solved √ )

[@miguelgnievesl6882]

Triangles ABC and ASR are similar due to their angles, therefore; If the ratio between the base and the height of triangle ABC is 4:5, then the same ratio applies to triangle ARS. Consequently, if the base = a then the height = 5a/4. Finally a + 5a/4 = 10. We obtain that a = 40/9.

[@marioalb9726]

then height = 4a/5 (not 5a/4)
Finally a + 4a/5 = 8 (not 10)
We obtain a = 40/9
or
then b-a = 5a/4 ( not height )
Finally a + 5a/4 = 10
We obtain a = 40/9

[@marioalb9726]

Similarity of triangles:
a / b = (h-a) / h
(h-a) = a. 8/10
Also:
(h-a) + a = 8
Replacing:
8/10 a + a = 8
a (1+4/5)=8
a= 8 / (1+4/5) = 8 / (9/5)
a= 40/9 cm

[@RAG981]

Label the side lengths, add up the areas =40. Works to give 40/9.

[@anthonyvalenti9093]

Well, I used area of triangle ars + area of trapezoid srcb.

[@sfratini]

Seems that you are assuming an acute triangle. Doesn't work for an obtuse triangle, unless I am missing something.

[@giuseppemalaguti435]

a=40/9

[@syedmdabid7191]

Eheu! Id est a= 40/9 unit. Responsimus.

[@yakupbuyankara5903]

a=40/9