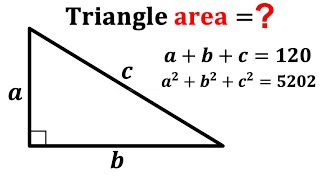
Can you find Perimeter and Area of the right triangle? | (Solve) |
ฝัง
- เผยแพร่เมื่อ 5 ก.พ. 2025
- Learn how to find the Perimeter and Area of the right triangle. Important Geometry and Algebra skills are also explained: Pythagorean Theorem; area of a triangle formula; perimeter. Step-by-step tutorial by PreMath.com
Today I will teach you tips and tricks to solve the given olympiad math question in a simple and easy way. Learn how to prepare for Math Olympiad fast!
Step-by-step tutorial by PreMath.com
• Can you find Perimeter...
Need help with solving this Math Olympiad Question? You're in the right place!
I have over 20 years of experience teaching Mathematics at American schools, colleges, and universities. Learn more about me at
/ premath
Can you find Perimeter and Area of the right triangle? | (Solve) | #math #maths | #geometry
Olympiad Mathematical Question! | Learn Tips how to solve Olympiad Question without hassle and anxiety!
#FindPerimeter #FindArea #PythagoreanTheorem #TriangleArea #GeometryMath
#MathOlympiad #IntersectingChordsTheorem #RightTriangle #RightTriangles
#PreMath #PreMath.com #MathOlympics #HowToThinkOutsideTheBox #ThinkOutsideTheBox #HowToThinkOutsideTheBox? #FillInTheBoxes #GeometryMath #Geometry #RightTriangles
#OlympiadMathematicalQuestion #HowToSolveOlympiadQuestion #MathOlympiadQuestion #MathOlympiadQuestions #OlympiadQuestion #Olympiad #AlgebraReview #Algebra #Mathematics #Math #Maths #MathOlympiad #HarvardAdmissionQuestion
#MathOlympiadPreparation #LearntipstosolveOlympiadMathQuestionfast #OlympiadMathematicsCompetition #MathOlympics #CollegeEntranceExam
#blackpenredpen #MathOlympiadTraining #Olympiad Question #GeometrySkills #GeometryFormulas #Angles #Height #ComplementaryAngles
#MathematicalOlympiad #OlympiadMathematics #CompetitiveExams #CompetitiveExam
How to solve Olympiad Mathematical Question
How to prepare for Math Olympiad
How to Solve Olympiad Question
How to Solve international math olympiad questions
international math olympiad questions and solutions
international math olympiad questions and answers
olympiad mathematics competition
blackpenredpen
math olympics
olympiad exam
olympiad exam sample papers
math olympiad sample questions
math olympiada
British Math Olympiad
olympics math
olympics mathematics
olympics math activities
olympics math competition
Math Olympiad Training
How to win the International Math Olympiad | Po-Shen Loh and Lex Fridman
Po-Shen Loh and Lex Fridman
Number Theory
There is a ridiculously easy way to solve this Olympiad qualifier problem
This U.S. Olympiad Coach Has a Unique Approach to Math
The Map of Mathematics
mathcounts
math at work
Pre Math
Olympiad Mathematics
Two Methods to Solve System of Exponential of Equations
Olympiad Question
Find Area of the Shaded Triangle in a Rectangle
Geometry
Geometry math
Geometry skills
Right triangles
imo
Competitive Exams
Competitive Exam
Calculate the length AB
Pythagorean Theorem
Right triangles
Intersecting Chords Theorem
coolmath
my maths
mathpapa
mymaths
cymath
sumdog
multiplication
ixl math
deltamath
reflex math
math genie
math way
math for fun
Subscribe Now as the ultimate shots of Math doses are on their way to fill your minds with the knowledge and wisdom once again.








Very clear steps with explanations,thanks.
You are very welcome! Thanks for the feedback ❤️🙏
Easy and solved it on my own.
Only difference is that I substituted a²= x first before solving
Given
AC= 6a²+11
AB= 3a²-2
BC= 7a²-3
A=?, P=?
a²= x
(6x+11)²= (3x-2)²+(7x-3)²
22x² -186x-108= 0
11x²-93x-54= 0
11 6
1 -9
Cross multiplied then added the factors to obtain -93
(x-9)(11x+6)
x= 9, -6/11
Since x > 0 in geometry
x= 9
a²= 9
a= 3
AC (hypotenuse) = 65
AB (height)= 60
BC (base)= 25
Area= 750 units²
Perimeter= 150 units
Excellent!
Thanks for sharing ❤️
Let's face this challenge:
.
..
...
....
.....
ABC is a right triangle, so we can apply the Pythagorean theorem:
AB² + BC² = AC²
(7a² − 3)² + (3a² − 2)² = (6a² + 11)²
49a⁴ − 42a² + 9 + 9a⁴ − 12a² + 4 = 36a⁴ + 132a² + 121
22a⁴ − 186a² − 108 = 0
11a⁴ − 93a² − 54 = 0
a² = {93 ± √[93² − 4*11*(−54)]}/(2*11)
a² = [93 ± √(8649 + 2376)]/22
a² = (93 ± √11025)/22
a² = (93 ± 105)/22
Since a²>0, the only useful solution is:
a² = (93 + 105)/22 = 198/22 = 9
⇒ AB = 7a² − 3 = 7*9 − 3 = 60
∧ BC = 3a² − 2 = 3*9 − 2 = 25
∧ AC = 6a² + 11 = 6*9 + 11 = 65
Now we are able to calculate the area A and the perimeter P of the triangle:
A(ABC) = (1/2)*AB*BC = (1/2)*60*25 = 750
P(ABC) = AB + BC + AC = 60 + 25 + 65 = 150
Best regards from Germany
Excellent job!
Thanks for sharing ❤️
To my mind it is easier to START with substitution x=a^2 than to apply it in the middle ;))
Excellent!
Thanks for the feedback ❤️
Technically speaking, it's not even necessary to use substitution, as it's not really a you're solving for, but a². Whether a = 3 or a = -3 doesn't affect the side lengths of the triangle, as a never appears as a direct component of their lengths. It only appears as a².
Let x = a^2
(3x - 2)^2 + (7x - 3)^2 = (6x + 11)^2
22x^2 - 186x - 108 = 0
11x^2 - 93x - 54 = 0
(x - 9)(11x + 6) = 0
x = 9, a = 3
Perimeter = 16x + 6 = 150
Area = (3x - 2)(7x - 3)/2 = 750
👍
After framing quadratic equation we will put a^2 = 9 t to reduce the coefficients
33 t^2 - 31 t - 2 = 0
t = 1 ( because it a^2 = 9 t)
Now t = 1 gives a^2 = 9
sides are 25 , 60 , 65
area = 750
perimeter = 150
Excellent!
Thanks for sharing ❤️
My way of solution ▶
In this right triangle ΔABC, we have :
[AB]= 7a²-3
[BC]= 3a² -2
[CA]= 6a²+11
By applying the Pythagorean theorem, we can write:
[AB]² + [BC]² = [CA]²
(7a²-3)² + (3a² -2)² = (6a²+11)²
49a⁴ - 42a² +9 + 9a⁴ - 12a² + 4 = 36a⁴ + 132a² + 121
58a⁴ - 54a²+ 13 = 36a⁴ + 132a² + 121
22a⁴ - 186a² - 108=0
Let's define a²= t
⇒
22t² - 186t -108=0
both sides divided by 2, we get:
11t² - 93t - 54= 0
Δ= 93²-4*11*(-54)
Δ= 11.025
√Δ= 105
t= (93+105)/2*11
t₁= 9
t= (93-105)/2*11
t₁= -6/11 ❌
t < 0
⇒
t= 9
⇒
a²= 9
a= 3
[AB]= 7a²-3
= 7*3²-3
= 60
[BC]= 3a² -2
= 3*3²-2
= 25
[CA]= 6a²+11
= 65
P(ΔABC)= 60 + 25 + 65
P(ΔABC)= 150 length units
b) A(ΔABC)= [AB]*[BC]/2
A(ΔABC)= 60*25/2
A(ΔABC)= 750 square units
Thank you!
You are very welcome!
Thanks for the feedback ❤️
Thanks easy ❤
شكرا لك من المغرب
You are very welcome!
Thanks for the feedback ❤️
Love and prayers from the USA! 😀
I did it the same way except I substituted x for a^2 before using the Pythagorean theorem rather than after. Either way results in the same answer.
Excellent!
Thanks for the feedback ❤️
(7a^2-3)^2+(3a^2-2)^2=(6a^2+11)^2
a= 3
b=3(3)^2-2=25
h=7(3)^2-3=60
A= 1/2*25*60 = 750
c=6a^2+11=65
P = 25+60+65 = 150
Solution:
Perimeter = (7a² - 3) + (3a² - 2) + (6a² + 11)
Perimeter = 16a² + 6 ... ¹
Area = ½ (3a² - 2) (7a² - 3)
Area = ½ (21a⁴ - 9a² - 14a² + 6)
Area = ½ (21a⁴ - 23a² + 6) ... ²
Pythagorean Theorem
[(3a² - 2)]² + [(7a² - 3)]² = [(6a² + 11)]²
9a⁴ - 12a² + 4 + 49a⁴ - 42a² + 9 = 36a⁴ + 132a² + 121
58a⁴ - 54a² + 13 = 36a⁴ + 132a² + 121
22a⁴ - 186a² - 108 = 0 (÷2)
11a⁴ - 93a² - 54 = 0
Let's consider a² = k
11k² - 93k - 54 = 0
∆ = (-93)² - 4 . 11 . (-54)
∆ = 8.649 + 2.376
∆ = 11.025
√(∆) = 105
k = (93 ± 105)/22
k' = -12/22 = - 6/11 Rejected
k'' = 198/22 = 9 Accepted
a² = k
a² = 9
a = 3 ... ³
Replacing ³ in ¹ to find the Perimeter
Perimeter = 16a² + 6
Perimeter = 16 (3)² + 6
Perimeter = 150 Units
Replacing ³ in ² to find the Area
Area = ½ [21. (3)⁴ - 23 . (3)² + 6)]
Area = ½ (21. 81 - 23 . 9 + 6)
Area = ½ (1.701 - 207 + 6)
Area = ½ . 1.500
Area = 750 Square Units
Thus:
Perimeter = 150 Units ✅
Area = 750 Square Units ✅
Excellent!
Thanks for sharing ❤️
STEP-BY-STEP RESOLUTION PROPOSAL :
01) Solving the Equation :
02) (7a^2 - 3)^2 + (3a^2 - 2)^2 = (6a^2 + 11)^2
03) Real Positive Solution : a = 3
04) Area = 60 * 25 / 2 ; A = 30 * 25 ; A = 3 * 250 ; A = 750 sq un
05) Perimeter = 60 + 25 + 65 ; P = 150 lin un
Thus,
OUR ANSWER :
Area equal 750 Square Units and Perimeter equal 150 Linear Units.
Super work!
Thanks for sharing ❤️
In triangle ABC: AC^2 = AB^2 + BC^2 or 36.(a^4) +132.(a^2) +121 = 9.(a^4) - 12.(a^2) +4 +49.(A^4) -42.(a^2) + 9, or 22.(a^4) -186.(a^2) -108 = 0,
or 11.(a^4) -93.(a^2) - 54 = 0. Delta = 93^2 +4.11.54 = 11025 = 105^2, so a^2 = (93 +105)/22 = 9 (the other possibility is rejected as beeing negative)
So a^2 = 9, and AC = 65, AB = 60, BC = 25. The perimeter of ABC is 65 + 60 + 25 = 150, and the area of ABC is (1/2).AB.BC = (1/2).60.25 = 750 (Easy.)
(I am always surprised to see how you solve second degree equations!)
It is really impressive how Premath solves the quadratic equations every time. Of course, the abc-formula also works, but using this approach avoids handling more inconvenient numbers in between.
@@unknownidentity2846 See the present example: How is it possible to guess that it is a good idea to use the fact that -93 = -99 +6 whithout knowing in advance that (x - 9) will be a factor, or if you prefer that 9 will be a solution? (If 9 is an evident solution, no need to factorize, it is quicker to use the product of the solutions to find the other one.)
@@marcgriselhubert3915 You are absolutely right. I think that took a lot of practice. On this channel I found an interesting video called “How to Solve Quadratic Equations using Three Methods - When Leading Coefficient is Not One” published in 2018 that shows how this approach works.
Best regards from Germany
Excellent!
Thanks for the feedback ❤️
I know the Pythagorean formula is easier, But, can the problem be solved using Heron's formula to find the AREA of the triangle and find the value of (a^2) or (a) and use that to find the PERIMETER?
Thé périmètre of triangle ABC IS
7a^2-3+3a^2-2+6a^2+11
P=16a^2+6
Thé area of triangle ABC IS
A=h×b/2
=(7a^2-3)(3a^2-2)/2
=7a^2-9a^2+6
A=-2a^2+6
P=150
S=750
Excellent!
Thanks for sharing ❤️
Triangle ∆ABC:
AB² + BC² = CA²
(7a²-3)² + (3a²-2)² = (6a²+11)²
(49a⁴-42a²+9) + (9a⁴-12a²+4) = (36a⁴+132a²+121)
58a⁴ - 54a² + 13 = 36a⁴ + 132a² + 121
22a⁴ - 186a² - 108 = 0
11a⁴ - 93a² - 54 = 0
11u² - 93u - 54 = 0 --- u = a²
11u² - 99u + 6u - 54 = 0
11u(u-9) + 6(u-9) = 0
(u-9)(11u+6) = 0
u = 9 | u = -6/11 ❌ u = a² ≥ 0
a² = 9
AB = 7(9) - 3 = 63 - 3 = 60
BC = 3(9) - 2 = 27 - 2 = 25
CA = 6(9) + 11 = 54 + 11 = 65
P = 60 + 25 + 65
[ P = 150 units ]
A = bh/2 = BC(AB)/2
A = 25(60)/2 = 25(30)
[ A = 750 sq units ]
Note that if one wishes to know the value of a, then it can be either 3 or -3. The usual requirement for a positive value of a variable involved in the dimensions of a polygon is unnecessary, as a only ever appears squared in the values. This is why I did not bother to solve for a, but rather a².
150
Thanks for sharing ❤️
a^2 quel intérêt ?
On the onset by inspection I automatically knew (a) around the perimeter was some form of the Number of the Beast, either 666 or 999. 😊
😀
That’s an interesting observation! 👍