วีดีโอ

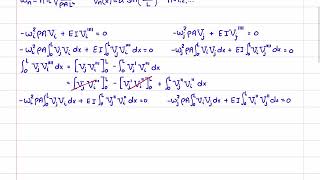
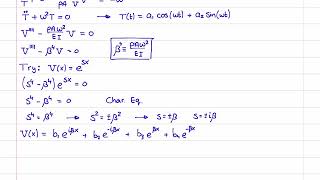
are you sure about the general Solution? Does that mean the system is unstable if c2 is not zero....I looked into other resources and I didn't see the same solution

Hi. Is the structure of your lessons for mechanical vibrations based on a specific textbook? If yes could you please name the textbook.

WOAH, this was your FIRST online course??? I absolutely loved how you taught it! I am sad you don't have lectures for the rest of my subjects! Or just more vibrations like with Fourier Series and such

❤❤❤

I feel like i've seen this guy in the "Have you seen this guy in your Sleep" posters

Is f0(t+1) a function or a variable*brackets?

What a beautiful writing

Thank you for the series. It was very helpful for studying dynamics 2 :)

Tks for sharing this course. :)

I hope to get 11/10 in 2 months, amazing videos!

Where does Ic=1/2mR^2 came from for homogeneous mass for the disc?

I very like these introductory lectures before the detailed lectures of each different concepts. Great way to motivate the students, and make the concept more intuitive during learning process. Thank you.

Thank you so much

hello is this beam subjected to a force or not if yes give me the value of this force

Great video! Thank you for explanation! Anyway, I didn't understand why the fourth deivative of Vi is canceled. Shouldn't it be replace with a terms that in some steps gives you the modal mass? Or maybe I just missed some assumptions. Sorry I'm trying to figure out the meeaning of modal mass on the beam

thanks, very clearly explained:)

Valuable videos🎉🎉

Great... Very helpful ❤❤

Thank you for sharing your knowledge on this subject! The explanations are clear and concise and very cleanly illustrated on the paper.

This is the best vedio I have seen on TH-cam. Thank you for your demonstration and thank you for your time👏

can you explain more the chain rule of calculus in this case please?

Natural frequency isnt it 1 over time? , 1/t=f

Can I know the program that u use to write like this plz

Which book do you follow sir

Which book do you follow

Hi Juran, Heel duidelijk uitgelegd. Top

Tanks a lot sir for making this course public. Is there any possible way to make the lecture notes available too? It can be so helpful to review the contents...

If the masses and sping constants are same in 1st problem, how the expression of kinetic and potential energy will vary? Please answer

Hi! Prof. Schilder, I am glad to learn about your mechanic vibration lesson, these lesson hello me a lot. to reduce the vibration amplitude of a centrifugal fan whose motor support bracket like a spider, I optimize the structure of the spider, which is like a cantilever system. I change the leg of spider structure from one beam to a trusswork, and the vibration amplitude was reduced. and I can't understand the relationship between the stability of structure and vibration amplitude. could you share me some know-how about this issue? may you have a nice day.

thank you for all the hard work you have put in.

Do you have MATLAB code to solve this?

Life saver

Thank you for the videos. They were very enjoyable and clear.

at 9:35 , why do you say that B^4 = (n^4pi^2/L^4) _times_ rhoA ..., should it not be *equal* to rhoA ...?

So, if I understand correctly, when integrating the delta function from 0 to L, we can always say it is equal to 1? Is that like saying you integrate from 0 to (L- to L+) as it is such a small piece of L? I am confused, as when evaluating the integral you get delta(L - L) - delta (0 - L) = 0 - delta (-L) , where -delta(-L) = infinite.

If i is j, why still write down Vj Vi, and not just Vi^2 or something like that?

What a ride! This whole course had its highs and its twits and turns, with me not getting it, but in the end the whole plot fell together wonderfully. Jokes aside, many thanks Professor Schilder for these lectures, a great series!

(Possibly stupid question) Shouldn't there be some sort of coefficients in from of each term U(x)\eta(t) so that the sum converges? I'm modeling some vibrations in a beam in MATLAB, and, without these coefficients in front, the first 10 terms appear not to capture ~99% of the variability, which, I would think the first 4 or 5 terms would ordinarily do so. TIA

So for X1, do you multiply the function by (1/m) / (1/m^2)?

Wonderful video series, sir! Thank you so much for your lovely exposition.

Do we just assume its an exponential? So choose e^(st) every time? or because it would be logical is the bullet was to slow down exponentially?

1) It looks like you are using the fact that the "differential equation operator" is self-adjoint (Sturm-Liouville theory), so eigenvectors corresponding to distinct eigenvalues are orthogonal (really a consequence of The Spectral Theorem) th-cam.com/video/12d15vI52b8/w-d-xo.html 2) "The Gram-Schmidt process is A Good Thing" (TM).

[OT] How, if at all, can all of this be simplified/streamlined by Laplace/Fourier transforms?

1) Super-great video series! Thank you so much. 2) I guess I'm used to seeing k as the symbol for the wave number, not \beta, but, if this is common usage, I'll get used to it.

watching this 3 years after you posted them and I have to say they are the best I've seen. please consider doing videos on other subjects. Thanks a lot!

thanks a lot! great!

thanks that is very helpful, really appriciate it

thanks a lot

Great Lectuve, thank you, but why do you take the second Partial derivative of v(x,t) with respect to t, for the acceleration term ? I would have take the total second derivative of v(x,t) with respect to t, for the acceleration, and develop this term using the chain rule. Would i find the same result if i do this ? I do not know if my question/probleme is clear.

I didn't get how the solution part works at 10:26 How did the quadratic eqn with s^2 + ... gets multiplied to the exponent and equated?