วีดีโอ

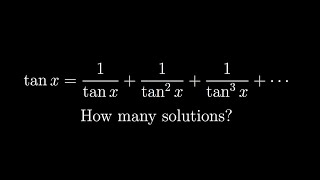
neat - also follows immediately from Descartes's rule of signs

We love the Calvin and Hobbes shirt!

P(x)=2x^5+8x-7 P'(x)=10x^4+8>0 for any x so by the consequence of Theorem of Lagrange for the interval (-inf,inf) P(x) is strictly increasing because P(x)>0. Because lim (x->-inf) P(x)=-inf and lim (x->inf) P(x) -> inf by IVT there exists a point where P(x)=0 I was expecting P'(x) to have roots as this would involve T Rolle and be more interesting

I like the work you did with option D, but I'm confused about how you came up with the inequality with the minimun of the function, integral of the function, and maximum of the function. Is that some truth or property of integrals? I've taken a calculus course, but its been a bit.

It only takes a few seconds to obtain 10! = 2^8 * 3^4 * 5^2 * 7 (I'll now talking terms of the antilogs of the choices) We can reject A and E because they don't have have a factor of 7 directly or indirectly. We can reject B because it only has a factor of 3^2 We can reject D because it has a factor of 3^(2 + 6 + 4) = 3^12 That leaves us with C. Check: it gives us (2^2 * 5^2)(2^2)(2^4 * 3^4)(7) = 2^8 * 3^4 * 5^2 * 7 as required.

I like your explanation for option D .. keep the good work

I just view it as adding up cylinders of base radius y and height dx so overall πy^2dx=π int(1/(1+x^2)dx) which is arctan from 0 to infinity and we get a π^2/2 result

didn’t understand the notation for D however i settled on E after remembering the cube root function

Your logic and reasoning was spot on. It is 1 solution. I got it wrong, said it was 2 solutions, I forgot |r| has to be <1, so did not reject one of the solutions

I see this infinite series being x+x^2+x^3+...=1/(1-x) when |x|<1 In this case |tan x| > 1 and tan(x)=(by condition) 1/tan(x) +1/tan^2(x)+...=1/(1-tanx) => tan(x)-tan^2(x)=1 or tan^2(x)-tan(x)+1=0 Tan(x)=(1+-sqrt(5))/2 we reject tan(x)=(1-sqrt(5))/2 because it is not smaller than -1 so we are left with one choice

4096*1.2 is in fact 4915.2, so your approach doesn't quite work at the end, but it's still clearly more than 4100, so that's good enough given the multiple-choice answers.

Happy New Year. Thanks for doing the question. It was UCLES A level Further Mathematics B 1, QP 9220/1, 1984, Q1. The given solution said, if ax³ + bx² +cx + d=0 then if the roots are α ß and Γ then α + ß + Γ = -b/a, αßΓ = -d/a and αß +αΓ +ßΓ = c/a. Equate that to terms of an AP n-d, n and n+d. That avoids a lot of the algebra you had to do. That leads to 3n = -p, 3n² -d² = q and n³ - nd² = -r. Then eliminate n and d to get answer

I think all of them are true. A) since the function is continuous it will be bounded B) from above the surface under curve will be finite C) another way of stating intermediate values all exist D) the average value of f(X) is between f(-2) and f(3) E) the function is continuous but necessarily derivable on the interval so f'(0) may not exist I thought all are true when I read it lol

Let P(x)=y=x^3+ax^2+bx+c with local extrema points (1,2) and (3,d) From T Fermat if a function admits a local extrema at a point c then f'(c)=0. In our case P'(x)=3x^2+2ax+b and consequently P(1)=0 and P(3)=0 so the polynomial can be rewritten with regards to it's roots as P'(x)=3(x-1)(x-3)=3x^2-12x+27 equating coefficients => a=-6 b=27 We additionally know P(1)=2 so 1+(-6)*1+27*1+d=3 => d=-19 so d=P(3)=27+(-6)*9+27*3-19=27*4-2*27+19=54-19=35

Ha ha! Based on the thumbnail, I did the entirely wrong calculation: log 10| = 2 + log( 3*4 * 6*7*8*9 ) = 2 + log( 12 * (55² - 1) ) - that's its own internet meme, for product of 4-term arithmetic sequence = 2 + log( 12 * 3024 ) - using mental-math shortcut for (10n + 5)² = 100*n(n+1) + 25 = 2 + log(36,288) = 5 + log(36.288) - but log(36) = 2*log(6) ~ 2 * 0.77 ~ 1.54 from my old E.E. courses ~ 6.54 + a bit more. As for the ACTUAL problem: 10! becomes (10*5*2) * (6 * 3 * 8 * 9) * 4 * 7 for 2 + 2 log 2 + 4 log 6 + log 7 => (c). It's a bookkeeping challenge - especially under pressure, whether of contest time or the camera. Easier when one is seated comfortably on the couch with a Christmas beverage.

Definitely needs to have prime factors in there Must have 2,3,7 for sure. Because we are using lg then we can rewrite lg 5= lg10/2=1-lg2 so we can skip 5. Because of this substitution the leading integer should be 2. In the factorial we can gather a total of 2^7 (excluding lg10) and 3^4 so we can compile 4lg6 and 3lg2 out of them -1 lg2 from converting lg5 so so 2+2lg2+4lg6+lg7. Looks like I am getting too lazy :)

That was fun! I used the same approach as you.

Here’s a (ultimately logically equivalent) solution that proceeds by identifying that certain algebraic combinations of a and d must be integers. Note: I take a to be the middle term of the sequence, which I think simplifies the algebra. The sequence (a-d), a, (a+d), is “special” if (a-d)^2 + a^2 + (a+d)^2 = a d^2 or (expanding and simplifying), 3 a^2 = (a-2) d^2. Note that 3 (a/d)^2 = (a-2) is an integer. In fact, since 3 is not square, a/d is an integer. Define r = a/d. Writing a and d in terms of r gives a = 3 r^2 +2 and d = a/r = 3 r + 2/r. By the second line, 2/r = d - 3 r and is, therefore, an integer. So r can only be 1 or 2, which correspond to the only two special sequences: 0, 5, 10 and 7, 14, 21.

Wow this problem formulation is interesting. I think I will select my 3 terms to have the form a-r,a,a+r with r>0 to have more symmetry. So the special series has the property (a-r)²+a²+(a+r)²=a*(r)² and we need the sum of all a+r possible 3a²+2r²=ar² Notation x(r)=a+r what we want to find => a=x-r and substituting back. 3(x-r)²+2r²=(x-r)r² 3x²-6xr+3r²+2r²=xr²-r³ 3x²-x(6r-r²)+5r²-r³=0 Delta=(6r-r²)²-4(5r²-r³)=36r²-12r³+r⁴-20r²+4r³=r⁴-8r³+16r²=[r(r-4)]² => x1,2= (6r-r²±√[r(r-4)]²)/6=(6r-r²±(r²-4r))/6 x1(r)=(6r-r²+r²-4r)/6=r/3 x2(r)=(6r-r²-r²+4r)/6=(5r-r²)/3 now the function x1(r) is a function defined on x1:(0,+inf)->(0,+inf) function x2 : (0,inf)->(25/6,-inf) seems like a whole lot of values if you ask me so I might be missing something. I see now the values are integers. Now that changes things... x1(r) is an integer if and only if r=3k , k belongs to N+ x2 is an integer also when x=3k or when 5-r=3l which means r=5-3l equivalent to r=-1+3k (mod 3) k>=1 in both cases. But the thing is there is still an infinite number of values I am probably missing some limiting conditions... 3a²+2r²=ar² implies lhs is positive and rhs must be positive so a>0 too so x must also be positive. I will verify if my solutions are good for the starting condition : Case 1: x=k r=3k , k>=1 integer => a=x-r=-2k for every k but a cannot be negative thus rejecting this posibility case 2: x=k(5-3k) r=3k => a=x-r=2k-3k² does not work even for k=1 a=-1 r=3 x=(-1+3k)(5-(-1+3k))/3=(-1+3k)(6-3k)/3=(-1+3k)(2-k)=-2+7k-3k² r=-1+3k so a=-1+4k-3k² when k=1 x=2 and r=2 so a=0 which is a possible solution when k=2 x=0 and r=5 so a=-5 which is not a valid solution for larger k x<0 so we reject So over the integers we have only a possible solution -2 , 0, 2 series I missed the statement saying we are looking at integers lol. I was prepared to pull off an integral or something

Nice. Pretty much what I did. The run up at the end can be reduced by observing the difference between two adjacent squares is always odd, while 24 is even and must be the sum of at least two of those. So for d = 7 and we've hit a difference of perfect squares exactly 2 apart, we are done.

I prefer the standard proof: 1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + ... > 1 + 1/2 + (1/4 + 1/4) + (1/8 + 1/8 + 1/8 + 1/8) + ... = 1 + 1/2 + 1/2 + 1/2 + ... which obviously diverges.

I will just show a classic usage of theorem of Laplace here. Let f(x)=ln(x) f: R+ -> R . As an elementary function it is continuous and derivable on (0,+inf) and subsequently on each interval [k,k+1] where k is a natural number. Since the prerequisites are satisfied from applying the Theorem of Laplace it follows that for each interval [k,k+1] there exists a number c such that k<c<k+1 and f'(c)=(f(k+1)-f(k))/(k+1-k) or 1/c=ln(k+1)-ln(k) (1) Now we are working on the inequality k<c<k+1 and raise it to power -1 => 1/k>1/c>1/(k+1) (2) from (1) and (2) => 1/k> ln(k+1)-ln(k)>1/(k+1) k=1 1>ln2-ln1>1/2 k=3 1/2>ln3-ln2>1/3 .... k=n 1/n>ln(n+1)-ln(n)>1/(n+1) Add everything up and simplify telescoping sum results in sum(1/i ; i=1..n)>ln(n+1)-ln1>sum(1/i ; i=1..n+1)-1 Taking limit as n-> + inf from the first part of the inequality results 1/1+1/2+1/3+...>lim ln(n+1) -> + inf so it diverges I watched the video and for your proof the integral should go from 1 to n+1 and you get the exact result from here. I was expecting the elegant showcase proof from math professors from below: 1 + 1/2 + 1/3 +1/4 +1/5+1/6+1/7+1/8+1/9+... series is always greater than the following sum 1 + 1/2+ 1/4 +1/4 +1/8+1/8+1/8+1/8+1/16+... because 1/4<1/3;1/8<1/5 and so forth But watching the series we have 2x values of 1/4 which add to 1/2 and 4x values of 1/8 adding to 1/2 followed by 8 vaules of 1/16 which also add to 1/2... This basically means that we can rewrite as 1+1/2+1/2+1/2+... -> +inf which means that the harmonic series which is larger also diverges

Number theory problems. It reminds me of when out math teacher was sick and we got replacement another class' math teacher who didn't bother to see how far we were into the curriculum and progress us trough 1-2 lessons But he gave us problems about last digit of power of x. My take away was that for any number multiplying by itself results in a loop of the last digit , which , makes sense since there are only 10 digits in decimal notation and they will repeat after a while :) So here we go 7^0=1 7^1=7 7^2=x9 7^3=x3 7^4=x1 so the loop repeats every 4 powers this means the last digit of 7^25=(7^4)^6*7=7

Quick trick from Olympiads can be used here - use the AM-GM inequality on the mean of 2y and z, where y and z are side lengths with 2y+z = x. This gives x/2 = (2y+z)/2 >= sqrt(2yz) ==> yz <= x^2/8. This more easily generalises to higher dimensions of other constraints.

well just area under parabola while taking out a triangle situated between x=a^2 , y=0 and tangent line at point (a,a^2) . line equation with a given slope is y-y0=m(x-x0) m=f'(a)=2a in this case so plugging in y-a^2=2a(x-a) y=2ax-a^2 which intersects x axis when y=0 so x=a^2/2a=a/2 Areatriangle=1/2b*h=1/2(a-a/2)*a^2=a^3/4 Area under parabola= 1/3 x^3 (evaluated between a and 0)=1/3 a^3 Final area=a^3/3-a^3/4=a^3/12

What program do you use?

this is a headscratcher i was jsut lookig at the text of the problem not knowing wtf to do. Inserting angles into it will make it awkward If we have sides 4,10 and letters a,b taken for interval I will use c as length of final side so this means s=sqrt(1/16(14+c)(6+c)(14-c)(-6+c)) so s=1/4sqrt((14^2-c^2)(c^2-6^2)) from this it results that 6<c<14 so that the square root exists and this does not account yet for the size of s => 16s^2=-c^4+(196+36)c^2-36*196 c^4-232c^2+16s^2+36*196=0 (36*196=(40-4)(200-4)=8000-4*240+16) (c^2-116)^2-116^2+8000-960+16+16s^2=0 (c^2-116)^2+90^2-116^2-100-960+16+16s^2=0 (c^2-116)^2-26*206-1060+16+16s^2=0 so 16(s^2+1)-1060-26*206 < 0 so that equality can take place if we call this expression -t^2 then (c^2-116+t)(c^2-116-t)=0 will have 2 solutions only when 116-t >0 and 116+t>0 so -116<t<116 so -t^2>-116^2 not sure i understand the problem. Maybe tomorrow when I am actually awake because what i got looks totally uncalled for

Why can't I take the the the hexagon sides as simple x? The remaining would be (1-x). So by like this, (1-x)^2 = x^2+x^2 And answer changes.

Nice reasoning!

Maximum area is always when half the fencing runs in each orthogonal direction. Here, that gives dimensions of (x/2) by (x/4) and thus A_max = x² / 8. In general: for a rectangular plot of width w and height h, where the fencing constraint can be modelled as a⋅w + b⋅h = f, then it's a few lines of algebra to show that A = - (a⋅w - ½⋅f)² / ab + ¼⋅f²/ab and hence the maximum area occurs when aw = ½f. Working through the proof makes a good challenge question for a pre-calculus class.

Let's consider the rectange having 2 sides L and l L>=l then it follows that x=L+2l and A(l,L)=l*L => L=x-2l => A(l)=l(x-2l)=lx-2l^2 as a quadratic wirh the coeffixient of l^2<0 it admits a maximum with the value of -delta/(4a) if quadratic is of the form al^2+bl+c So max=-(x^2-4(-2)*0)/(4*(-2))=x^2/8

I appreciate the fact that you didn't edit the video to delete the mistake, which actually shows that these things happen and it's better to just start over. Thanks!

Hi, HCF is the ploynomial with the highest degree that occurs in both. You could also have divided the polynomials, and sort of used the Euclidean algorithm and keep going until remainder is zero, like you would with two integers. Thanks for doing the question. Reason I submitted question was I had not seen HCF of polynomials before, only using algorithm for integers before.

Nice problem

since the cubic polynomials have a single real root, the other two roots are complex conjugate, so they share both roots, so we can write the polynomials as (x+20)(x^2+ex+f) and (x+21)(x^2+ex+f), expanding this out and using the fact the quadratic term is zero in the first we get e=-20, and then using the fact that the linear term is zero in the second we get that f=420. Now a simple application of the quadratic formula gives us that m=20/2, n=420-100=320, so the sum is 330

This seems like it would take some calculations. If we use vietas formulas this thing looks very ugly... I will use n instead of √n in my calculations From first poly roots -20,m+ni,m-ni Coeff x^2:-20+2m=0 Coeff X: -20*2m+m^2-n^2=a Free coeff: -20(m^2+n^2)=-b -20^3-20a+b=0 -8000+800m-20m^2-20n^2+20(m^2+n^2)=0 -8000+800m=0 so m=10 From second polinomial -c=-21+2m=-1 => c=1 -d=-21(m^2+n^2) -21^3+21^2c+d=0 -21^2*20+d=0 d=20*21^2=21(m^2+n^2) 20*21=100+n^2 n^2=420-100=320 n=√320 According to original problem sum of Re+im^2=330

Surely this is too easy right?

Quite a few questions like this in MAT. If you use cos­²x= 1-sin²x, then complete the square in the quadratic, using a subsituition like sinx=y like you did if you want, max is 13/3.

Isn't such a matrix always of the form ( a b ) ( b a ) ? That makes it even more obvious.

Well all variants of A have the form (a k-a) (K-a a) So rows and columns add to k Det(A-lambda*I)=0 means the eigenvalue lambda should be k-2a to result in zero determinant Let V(X) (Y) Be an eigenvector of A A*V=lambda*V ( a. k-a). (X). (X) (k-a. a). *. (Y). =. (K-2a)* (Y) aX+(k-a)Y=(k-2a)X (k-a)X+ay =(k-2a)y (a-k)X+(k-a)y=0 => X=Y for eigenvectors So only column vector (1,1) works

I did it the same way on the first go. Then, while watching, a slightly different way occurred to me, to give greater confidence. Here, due to the symmetry of the expression: five ways to assign 3, then four ways to assign 1, and two thirds of the remaining six possibilities are divisible by 3, simultaneously counting both the successes and failures. This yields 80 and 40 together, correctly summing to the required 120.

i just did the sum from n=1 to 50 of ((2n-1)^2 - n^2) this factors out to just n=1 to 50 of (-4n+1) so using -4n(n+1)/2 +50 with n= 50, you get -5050

There are 5 ways to pick the number which has value 3 but it may be irrelevant in the end... Let's sat x1=3 then all products containing x1 will be divisible by 3 and for the whole sum to be dividible by we require X2*x3*x4+x3*x4*x5=x3*x4*(x2+x5) to be disicible by 3 which is only achevable when x2 and x5 add to a multiple of 3 which can be 1+5 ; 5+1; 2+4;4+2 total of 4 ways of choosing the pair and then 2! Ways to choose the last two numbers Answer 5*4*2=40 Random observation 40=5!/3

A fun one! One thing I think is noteworthy @ 9:21 is that we see y and x must share a factor (so when together they make a perfect prime), so x, y, root xy all share that factor, therefore, that factor must be 11.

Wow the trig thing looks super tedious Btw sin(-2arctg(2t))=-2*tg(arxtg(2t))/(1+tg^2(arctg(2t))=-2*2t/(1+4t^2) cos(-2arctg(2t))=cos(2arctg(2t))=(1-tg^2(arctg(2t))/(1+tg^2(arctg(2t))=(1-4t^2)/(1+4t^2) This comes from the identity used for Weierstrass substitution when you set tg(x/2)=t then sin(x)=2t/(1+t^2) and cos(x)=(1-t^2)/(1+t^2) Even so getting the final result is going to be really annoying haha

You nailed it at 27:05: "This vector points straight up". 😉 Very nice work-through. I've solved this one with algebraic geometry, but without the use of trig in this way. I suspect I was working more with reflections (given my physics background) than rotations, but memory fails me in such detail after all these years. Perhaps I'll give that another go and post here what I get. After a half century of being haunted (in a good way, I guess) by this problem, I officially discovered the "official solution" a few weeks ago. That is (more concisely than I worked it through) described in another comment. A third approach is to use the well known fact that a light source at the focus of a parabola beams light to infinity parallel to the axis of symmetry; and, most importantly, vice versa. Thus the image of the fixed focus, in the contact point tangent, must be vertically above the point of contact along the reflection of the incident beam. That, plus the focus-directrix definition of a parabola, is sufficient to put the locus as the directrix of the fixed parabola. I stumbled on this solution a few years ago revisiting this problem. Then there is the projective geometry solution that, in the panic of the last few minutes before lunch as my algebra wasn't working out, I quickly wrote up. Namely, that if it was hyperbola on hyperbola the locus must curve upwards to infinity; and if it was ellipse on ellipse the locus must close down, but increasingly further out and less curved as the eccentricity increased. Until, in the limit of a parabola (that is, an ellipse with infinite eccentricity) the locus cannot close either up or down, and must hence be a straight line (that being the directrix of the fixed parabola). I've often wondered just how many marks I got for submitting that, with great confidence.

Wow this looks like an amazing problem. I will give it a try on paper tomorrow before posting my ideas and watching the video My basic idea is that by drawing the tangent line in the point where the 2 parabolas meet the length from vertex to tangent point will be equal for both and they will be mirror images of eachother with respect to the tangent line. So by mirroring the focus of the basis parabola y=-x^2 through the tangent line in a generic point we will find the position of the focus of the rotating parabola and the relation of the geometric locus. From the problem it results the negative parabola has focus of (0,-1/4) y=-x^2 => dy/dx=-2x => Tangent lines have the form at a point (p,-p^2) knowing slope will be -2p -2p=(y+p^2)/(x-p) y+p^2=-2px+2p^2 y=p^2-2px We need to find the point (a,p^2-2pa) such that the distance to (0,-1/4) is minimal then we double the vector sides to locate the other focus f(a)=(a-0)^2+(p^2-2pa+1/4)^2 is minimal f(a)=a^2+4p^2a^2-4pa(p^2+1/4)+(p^2+1/4)^2 As a parabola the point which satisfies the conditions is -b/2a for a normal equation translating into 8p(p^2+1/4)/(1+4p^2)=2p So the point we are looking for on the tangent line is (2p,-3p^2) Rolling parabola focus should be (0,-1/4)+2*((2p,-3p^2)-(0,1/4))=(4p,-6p^2+1/4) => y=-6p^2+1/4=-6/16(4p)^2+1/4=-3/4*x^2+1/4 But by reading comments I know this is not right

That was very impressive, well done. Way beyond my abilities!!. Since you said where the question was from, I looked up on-line. It said: Answer: horizontal line y = 1/4. The tangent to the fixed parabola at (t, -t2) has gradient -2t, so its equation is (y + t2) = -2t(x - t). We wish to find the reflection of the focus of the fixed parabola in this line, because that is the locus of the rolling parabola when they touch at (t, -t2). The line through the focus of the fixed parabola (0, -1/4) and its mirror image is perpendicular to the tangent and so has gradient 1/(2t). Hence its equation is (y + 1/4) = x/(2t). Hence it intersects the tangent at the point with y + t2 = -4t2(y + 1/4) + 2t2 or y(1 + 4t2) = 0, hence at the point (t/2, 0). So the mirror image is the point (t, 1/4). t can vary from -∞ to +∞, so the locus is the horizontal line through (0, 1/4). Still not sure I understand the last bit of that! 🤣

My line of thought with out anything [ pen/paper/writing ]. Step 1. (266) ^ 3/2 = (sqrt(266))^3 ~= (16.2)^3 ~= 256*16.2 ~= 4000+ (definitely). Call this result p. Step 2. p * sqrt(1.5) ~= 1.35ish * p ~= 1.35 * (>4000) ~= 5.2 or 5.3K. Answer is 5300.

Simplifies to 266 * sqrt(1.5 * 266), which is 266 * sqrt(399) giving about 266 * 20; so (E).