วีดีโอ

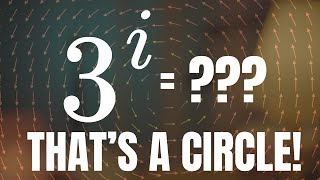
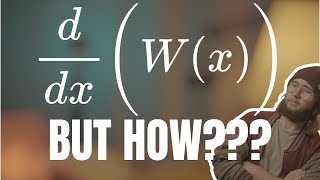
A like for the choice of example sin(x)/x which links Feynman's Trick with Laplace Transform

nice

Glad i found a man of intrest like me!

Man I am in Highschool and i really loved your videos, please make on this more. We both share a common passion of mathematics

Nice explanation about Feynman's trick! But why are you saying "innegral" but not "in-roduce"? Greetings from a German fella, who's getting desperate about the Americans' refusal to pronounce the letter "t"

we can also write L as exp(-ln(x)/x) and since exp is continuous we can apply the limit as x goes to infinity and we get 1

So, what the trick is about is that you want to bring Mr. F up in x land. So you first give him a friend in t land and their friendship, G is in x and t land. Then you take their friendship down in t land, then up in x land and up in t land. You've gone down and up in t land, so that's fine, and you've gone up in x land, which is what you wanted. (in other words, integrating with respect to t commutes with integrating with respect to x, so you just do it in the other order)

loved it!

last problem is less messier using the normal induction too..

really one of the best lesson i had seeing the intuition for solving problem which none of the other do like u did thats the most essential thing u taught Thankyou sir!! Hoping more other such video

THAT RICHARD FEYNMAN WAS ONE SNEAKY TRICKY OLE BASTARD. HE WAS A T. O. B. --- TRICKY OLE BASTARD ---

what an interesting approach and presentation, you are a rare diamond in a single copy!

We need a symbol for the differentiation method to distinguish it from the integration approach. Mathematicians give mixing the notations used to represent the differentiation and integration methods. For instance lecturers state of performing integration of parts, not knowing they will be performing derivative. For derivative: u(x) ≈ xu^(x-1) and for integration: n(x) = (1/(x+1)*n^(x+1).

Ginus Feyman !

58 is not a multiple of 7

the second problem can also be solved using cauchy-schwarz inequality!!

wow that last problem was crazy 🤯

Hello, I think you have a mistake in the 5th problem - the inequality doesn’t hold for n=1. You would’ve probably spotted this, but sadly, in the part where u did the AM-GM, the sum from 1….n-1 is actually n(n-1)/2, since we have only n-1 numbers in the sum. Due to this unfortunate mistake, you got the answer a^(n/2), but actually, you should’ve got a^((n-1)/2). An easy fix would be to just make the inequality in the statement greater or equal, then everything will be just fine! Thank you for the vid, I’m enjoying this series a lot.

awesome neat

thanks for the video! everything just made sense once u plugged in y = -x. Please continue with this content i beg u 🙏🙏

yeah no I give up, I'm not smart enough for maths 😭

Nice

Awesome video i'm really really sad you stopped posting vids 😭 hope ur okay bud

This method is NOT called "Feynman Integration" , IT'S CALLED *Leibniz Integral Rule* . Gottfried Leibniz DISCOVERED THE RULE, Feynman POPULARISED IT. THIS IS Leibniz's technique, NOT FEYNMAN'S. GIVE THE CREDIT TO THE RIGHT PERSON FOR GOODNESS SAKE 😡😡 0:29 - You meant, " With a little bit of help from *GOTTFRIED LEIBNIZ* " 😡😡

Amazing format! I love the video format. Great work brother ^_^ Keep shining 😎

"IMO used to be easy". 😂You could say that again. Thank you bro, understood everything.🙏🏾

Sir, you are underrated!! please don't let the lack of views demotivate you!

OUTSTANDING explanation!

cool video, make more

It's Amazing how Feynman so frequently receives credit for this technique when it is actually attributed to Gottfried Leibniz. He wrote about it in a letter to Johann Bernoulli long before Feynman was even born. It seem a bit unfair to call it Feynman's Trick rather than the Leibniz integral rule. While Feynman was quite brilliant, he didn't invent this technique, he just read about it in a textbook (_Advanced Calculus_ by Fredrick S Woods) when he was a teen and then popularized it when he was at MIT. Feynman mentions this in his book, _Surely you’re joking, Mr. Feynman_. He never wanted to take credit for it. But for some reason, lots of people on the Internet treat this idea as if it were Feynman's original idea, which simply isn't true.

Amazing video, surprised this through explainer doesn't have more view, cheers 🎉

ej Ty jesteś z PL cn? bo widziałem twoje tt z e8

nice subject, this an outstanding problem solved by the same method enjoy !!!! th-cam.com/video/QReQpPhcIhA/w-d-xo.html

Simplify it by the identity e^W(x)=x/(W(x))

where have you been bro😢

literally the best frickin video on this topic and super fast too thank you so much

Thank You!

Why don’t I see this last year?

I really appreciate that this video’s randomly popped up on my feed. I can’t even understand fully how to use hölder. Thanks so much 😊

I might be stupid, but in 5:30 onwards, wouldn't plugging in t=infinity for e^xt/x just give infinity rather than 0?

You find the homogene result then say that the particular answer is A(t)exp(-4t),put it in the equation,and then find the answer for A(t) doing a basing integration much more easier than doing the inverse Laplace transform

Cool

Very nice

Very clearly explained! Thanks so much!

nice one bro

Amazing video! Your explanations are always on point, and the visuals are great at complementing them (as well as being marvelous to look at).

Brother you keep making my calc classes infinitely easier, much love

best math channel out there that I could discover. !!!!!!

Awesome video bro