Solving quadratic equations by completing the square
ฝัง
- เผยแพร่เมื่อ 17 ม.ค. 2025
- This algebra tutorial covers two examples of solving non-factorable quadratic equations by using the completing the square method. This is a must-learn method for your algebra, precalculus and even calculus classes. Be sure to check out completing the square introduction 👉 • Completing the square ...
Subscribe to @bprpmathbasics for more algebra tutorials.
Shop my math t-shirts & hoodies on Amazon: 👉 amzn.to/3qBeuw6
-----------------------------
I help students master the basics of math. You can show your support and help me create even better content by becoming a patron on Patreon 👉 / blackpenredpen . Every bit of support means the world to me and motivates me to keep bringing you the best math lessons out there! Thank you!
-----------------------------
#math #algebra #mathbasics


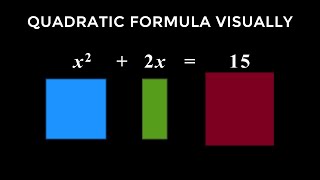






Where did the quadratic formula come from?
Here's the answer 👉th-cam.com/video/AD58TWGIcsQ/w-d-xo.html
It's magic - no human can do that. I'm talking about a seamless marker switch.
I never used this one
it was always factoring or formula
Here is a riddle that leads to a non factorable equation: Think of a positive, real number (Φ), subtract 1 from it (Φ-1), invert the results [1/(Φ-1)], and you get back that number [Φ=1/(Φ-1)]. What is that number?
The golden ratio.
x = 1 + \frac{1}{x}
x^2 = x + 1
x^2 - x = 1
Now this is a quadratic equation, so we can complete the square.
(x - \frac{1}{2})^2 = \frac{5}{4}
x - \frac{1}{2} = \pm\sqrt{\frac{5}{4}} = \pm \frac{\sqrt{5}}{2}
x = \frac{1}{2} \pm \frac{\sqrt{5}{2} = \frac{1 \pm \sqrt{5}}{2} = \phi
If you don't understand LaTeX notation, \frac{x}{y} just means x/y, \sqrt{x} means the squareroot of x, \pm means plus or minus, and \phi means the Greek letter phi (Φ)
How is this non factorable?
@@user-dh8oi2mk4f Because you can't factor it
If we could factor x^2 - x - 1, then we could put it into the form (x + a)(x + b), which equals x^2 + x(a+b) + ab. This means ab must equal -1, while a + b = -1 which is not possible
@@user-dh8oi2mk4f x(x-1) = 1 => x^2 - x - 1 = 0 which is not factorable since there is no way of expressing the -x as two parts with coefficients that sum to -1 and have a product of -1 (i think) also bcz it doesn't have rational roots and nobody wants to factorise irrational roots unless they do
@@videogamemusicguy4208 “not factorable” and “not factorable over integers” are 2 completely different statements, and the first one is just wrong here
I would say much easier way to solve non factorable quadratic equation is to use Sridharacharya formula x={-b+-(b^2-4ac)^1/2}/2a for equation ax^2+-bx+-c=0. Sorry it looks funky in the comment but I really can't write it here the proper way. But you can try it, you will get the same result.
Good series!
Thank You.
I always liked if started with thinking x^2 - t * x + p = 0
T is the total of the roots, and P is the product of the roots and let H = half of t (so average of the two roots); Note alternating signs in original formula. Based on Vieta's formulas.
x = H +- ( (H)^2-p ) ^ (1/2)
Since the first problem had -10, I knew half was 5, which is the number you had before the +-, and under the radical is 5 * 5 - 4 = 21. Can do in head. Second one is a bit longer since you have a 2 at the start, H is -3/4 can be seen quickly, square it is 9/16 - (-3) will get you what is under the radical.
That is an interesting method I have never seen before. Pretty much, if it couldn't easily be factored, we just threw it into the quadratic equation. I didn't know there were other methods beside that.
I've always wondered if this is actually faster than just using the quadratic formula
Not when you use it in this strange "factoring" way.
But if you use actual completing the square thing - lots of times it is. But for that to be faster, I believe, you need to understand why it works. This guy did not explain it neither in this, or previous videos, so it might be hard to achieve just by his videos.
But in general, when you have 1*x + cx + d = 0, where c and d are some constants it's faster, then quadratic formula.
This guy is awesome.
I am giving you a challenging question....
"Find out the three different natural number which addition is same as their multiplication.. but challenge is that to find the values by only using maths , must make complete sense.. without using any guessing methods like Newton's method "
Call the three natural numbers a,b,c
we'll have: a+b+c=abc
Because a, b, c can change values to each other without affecting the problem
so let's assume a>=b>=c
-> 3a >= a+b+c
-> 3a >= abc
-> 3 >= bc
since b,c are natural numbers
so bc=0 or 1 or 2 or 3
if bc=0 then a=b=c=0
if bc=1 then b=c=1 and a+1+1=1.1.a (does not exist a)
if bc=2 then b=2 and c=1 so a+2+1=a.2.1 so a=3
if bc=3 then b=3 and c=1 so a+3+1=a.3.1 so a=2 (wrong because a>=b>=c)
So (a;b;c)=(0;0;0) or (3;2;1) and other permutations
@@o_o2688 actually I did the same way ...but here we need to put the different values to get the proper solution, but what I think is to find a method to get the values directly as an parametric equation in only one variable in that all the values can be calculated... But i think the type of method i want is not exist...😅😅..
Thanks for your reply...
@panchamsrivastava7386 I know that too, but I want a perfect method to get those numbers as solution, I don't want to do brute force like method
@@b77vedantmore51the word you’re looking for is “rigorous”
I prefer to do it as (x-5)² - (-5)² + 4 = 0, then simplify and solve but this method works too I guess
What do you do if its a Y and not a 0 on the other side of the equals sign
I like to put in blanks until I've factored the square, then work backwards to see what goes in the blanks.
So from x²−10x=−4, I write x²−10x+_=−4+_ and then (x−_)²=_. Now I look at the (x−_)² and try to expand it out. I get x²−2_x+_², but I don't write that down; I think about it while looking at the x²−10x+_ above.
So the blank in (x−_)² must be 5; fill that in. Then the blank in x²−10x+_ must be 25. So the blank in −4+_ must also be 25. Now I have (x−5)²=21, and I continue from there.
Nice 👍
Pretty cool, but where does that (1/2×a)² where a is the coefficient of x comes from?
Can you show how to do a square root of an imperfect square manually? I have looked it up in the past and failed to find a suitable explanation.
In practice, what people did before calculators, was use a slide rule. You could use the change-of-base rule, to write x^y = e^(ln(x)*y). Let y = 1/2, for square rooting.
The slide rule has features for calculating ln(x), where x would be the square rooted input. You'd then divide that by 2, to account for the exponent of 1/2. Then, use the other slide rule to calculate the exponential function.
There are many other methods, like Heron's method that I think would be the easiest to remember:
en.wikipedia.org/wiki/Methods_of_computing_square_roots
There's a method that looks similar to long division, which you can use to calculate the answer precisely to any number of digits. It's in the Wikipedia article that @@carultch linked, under "Digit-by-digit calculation", although you have to scroll past some theory to get to the actual description and a worked example.
Division.
It should be taught in school tho.
@@tobybartels8426 Did that a few times in the 80's when basic calculators started at 50 dollars or more. It is a slog. Pairing off digits and testing a few because sometimes you guess wrong, and are to large of a number.
So, the original equations can't solve for X with conventional maths like basic or algebra?
what will be the answer of √-2^2 a)-2 b)2i c)2
Depends on whether the square part is inside or outside the square root. If it's √-̅2², then it's (i√̅2)² = -1*2 = -2. If it's √̅-̅2̅² , then it's √̅-̅4 = -2i. (And if it's √̅(̅-̅2̅)̅², you get √̅4 = 2.)
Whatever works work
why is the second equation non_quadratic ,never had this in school
I am confused. Just use -p/2 +- sqrt(((p/2)^2)-q) and you get your x1 and x2. You learn that formula early on in germany. You get 5+- sqrt(21) in the very next step
That's the quadratic formula; in the USA, we learn it as (−b±√(b²−4ac))/(2a) (but with horizontal bars so no brackets are needed). Completing the square is worth knowing, however, because it can be used in other situations, such as finding the standard form of an equation for a conic section.
Another reason for knowing completing the square, is integration and Laplace transforms in calculus, when working with irreducible quadratic denominators. It's easy to integrate the function 1/(x^2 + 1), because the given expression directly matches the derivative (opposite operation of integration) of arctangent. However, what if you were given 1/(x^2 + 6*x + 10)?
It turns out, we can transform this expression to look like 1/(x^2 + 1), by using the method of completing the square.
x^2 + 6*x + 10 = (x + 3)^2 + 1
This means we can write it as:
1/((x + 3)^2 + 1)
Now it is just a horizontally shifted version, of an integral we know evaluates to arctan(x). Thus, the solution is arctan(x+3) + C.
The US does not teach the method based on Vieta's coefficients.
if you have x^2 + px + q = 0, and to make it easier to read I usually create an h = p/2 (which is the negative average of the two roots, while -p is the total of the two roots) the formula becomes
-h plusMinus sqrt (h^2 -q)
Edit the - and the plus minus sign causes odd printing
Dude pls reply me
..Will it work for any quadratic equation? 😢 It's so easy for me...😊
Hi teacher, can you prove to us that[ -sin(x) = cos (x+π/2) ]
Please and thanks
Rewrite them using Euler's formula:
e^(i*x) = cos(x) + i*sin(x)
Construct one with the negative input, and subtract one from the other, to determine what sine is, as an equivalent exponential:
e^(-i*x) = cos(x) - i*sin(x)
e^(i*x) - e^(-i*x) = cos(x) + i*sin(x) - [cos(x) - i*sin(x)]
Simplify, and solve for sin(x):
e^(i*x) - e^(-i*x) = 2*i*sin(x)
sin(x) = -i*[e^(i*x) - e^(-i*x)]/2
Do the same, for cos(y). But add, instead of subtract to solve for cos(y):
e^(i*y) = cos(y) + i*sin(y)
e^(i*y) + e^(-i*y) = 2*cos(y)
cos(y) = [e^(i*y) + e^(-i*y)]/2
Let y = x + pi/2:
cos(x + pi/2) = [e^(i*(x + pi/2)) + e^(-i*(x + pi/2))]/2
Use properties of exponents, to separate terms:
e^(i*(x + pi/2)) = e^(i*pi/2) * e^(i*x)
e^(-i*(x + pi/2)) = e^(-i*pi/2) * e^(-i*x)
Evaluate e^(i*pi/2) and e^(-i*pi/2):
e^(i*pi/2) = i
e^(-i*pi/2) = -i
Thus:
e^(i*(x + pi/2)) = i*e^(i*x)
e^(-i*(x + pi/2)) = -i*e^(-i*x)
Add together, and pull the i out in front:
cos(x + pi/2) = i/2*[e^(i*x) - e^(-i*x)]
Recall out earlier expression for sin(x), which is this the negative of the above expression:
sin(x) = -i/2*[e^(i*x) - e^(-i*x)]
Conclusion:
cos(x + pi/2) = -sin(x), QED
@@carultch thanks ✨
use cos(a+b) identity
Is it just me or completing the square is just general form of equation of the circle, like the steps
No. But, if you have an equation in both x and y which represents a circle in the cartesian plane, then you can use completing the square to bring this equation in a standard form
(x − p)² + (y − q) = r²
which lets you find both the centre and the radius of the circle, because this equation represents a circle with centre (p, q) and radius r.
That is value of e written in back 😂
I think Delta method is easier than this
Your notation is quite chaotic and unnecessarily complicated for students trying to learn the technique of completing the square.
For monic quadratic equations, just half the coefficient, here −10, of the linear term and then add and subtract its square, here (−5)² = 25, like this
x² − 10x + 4 = 0
x² − 10x + 25 − 25 + 4 = 0
(x − 5)² − 25 + 4 = 0
(x − 5)² = 21
x − 5 = √21 ⋁ x − 5 = −√21
x = 5 + √21 ⋁ x = 5 − √21
Of course, after a while and with some practice, you can skip the second step.
For nonmonic quadratic equations, you can avoid the use of fractions until the very last step by using Sridhara's method, which starts by multiplying both sides by four times the coefficient of the quadratic term before completing the square. Note that with this method, we add and subtract the square, here 3² = 9, of the coefficient, here 3, of the linear term of the _original_ equation, like this
2x² + 3x − 6 = 0
16x² + 24x − 48 = 0
16x² + 24x + 9 − 9 − 48 = 0
(4x + 3)² − 9 − 48 = 0
(4x + 3)² = 57
4x + 3 = √57 ⋁ 4x + 3 = −√57
x = (−3 + √57)/4 ⋁ x = (−3 − √57)/4
Here, with some practice, you can skip the third step.
Important step for it to not be complicated and chaotic like in the video is to understand why does it works, and he misses that point in both videos.
When you know that (a +- b)^2 = a^2 +- 2ab + b^2, and therefore 10x is the 2ab (where a is x), you can easily do it like you wrote.
He does not explain this, so he needs this factoring thing to determine what the square actually will be.
His notation is less complicated than yours. But, yes, it would be nice if he'd explain where the "magic number" comes from.