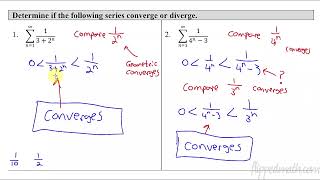
Calculus BC - 10.9 Determining Absolute or Conditional Convergence
ฝัง
- เผยแพร่เมื่อ 6 ก.พ. 2025
- Buy our AP Calculus workbook at store.flippedm...
For notes, practice problems, and more lessons visit the Calculus course on www.flippedmath...
This lesson follows the Course and Exam Description recommended by College Board for *AP Calculus. On our website, it is found under Calculus Version #1.
*AP® is a trademark registered and owned by the College Board, which was not involved in the production of, and does not endorse, our videos or our website.