Line Integrals: Full Example
ฝัง
- เผยแพร่เมื่อ 8 ก.พ. 2025
- FULL VECTOR CALCULUS PLAYLIST: • Calculus IV: Vector Ca...
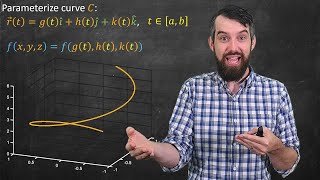
This video is a fully worked example of a line Integral. We use the Line Integral formula to compute the Line integral of a function f(x,y) over top of a circle of radius 2. We first parameterize the curve, then write the function in terms of that parameter, and then substitute into the formula.
My first video that introduces the idea of line integrals is here: • What is a LINE INTEGRA... )
OTHER COURSE PLAYLISTS:
►CALCULUS I: • Calculus I (Limits, De...
► CALCULUS II: • Calculus II (Integrati...
►MULTIVARIABLE CALCULUS (Calc III): • Calculus III: Multivar...
►DIFFERENTIAL EQUATIONS: • How to solve ODEs with...
►DISCRETE MATH: • Discrete Math (Full Co...
►LINEAR ALGEBRA: • Linear Algebra (Full C...
OTHER PLAYLISTS:
► Learning Math Series
• 5 Tips To Make Math Pr...
►Cool Math Series:
• Cool Math Series
BECOME A MEMBER:
►Join: / @drtrefor
MATH BOOKS & MERCH I LOVE:
► My Amazon Affiliate Shop: www.amazon.com...
SOCIALS:
►Twitter (math based): / treforbazett
►Instagram (photography based): / treforphotography








Bro, you're one of the most formidable teachers I've ever met. Thanks for these lessons!
I really can't believe that these videos are free to watch. God bless you, and your family!
Your lecture series is really awesome.
Please make a series on conics section that will help lot of students
Currently a student over zoom in Calc 3. I have no idea what the book is saying. YOUR VISUALS ARE SAVING ME! Thank you sir 🥳
Exactly the same thing, we learn with Soviet textbooks and they are obscure
this is pure Gold...never understood line integral this deeply...thank you so much professor
Can't describe how much I appreciate this, I have my Multi-variable calculus exam in a couple of days and your videos is just what I need. Great animations, visuals and explanations!
Thank you and good luck!!
I am on a liking streak. thanks for these videos.
I like your liking streak!
Taking Mathematical Physics right now and these videos really help brush off the dust from those old calculus topics I learned a while back. Thank you so much :)
Thank you for your lessons! I just love how lively you are and how you explain things step by step! Truely saving my university life
These types of videos are life savers my dude, you earned a subscriber that's for sure.
On a side note, maybe we are maybe a bit of a spoiled generation, with all the fancy computer graphics and great teachers the can feed us this knowledge with a spoon (it's like having the best privet teachers at your disposal always), which (IMO) actually hurts the solidification of this knowledge when you studying it for the first time (because you face less obstacles), but on the other hand, when you actually know this stuff, these videos are amazing to deepen intuition and refresh subjects quickly when they are relevant.
Anyway, sorry for the mumbling, thanks for the great videos, i give you my respect a simple engineering student who tries his best to deepen his understanding of math.
I stand up and salute you, by far the best calculus teacher i`ve ever known
these videos are great, as im following a vector calculus course now, and there is some concepts and things that i have been taught in other courses, that i have somehow missed or forgotten, and those concepts and things are also explained here
Its important to analyse the topics visually than in equations...... Thanks for making it clear
Glad you liked it!
This is amazing, the visuals and you are a genius teacher.
I am a physics teacher.
No one can teach better than you thank you so muchh sir
sir, you are a godsend
Thanks Herr Doktor.Beautiful explanation.
You’re most welcome!
I think your video is enough rather than a book 🙏🙏🙏
that's really awesome explanation....I think you are born to be a teacher.
really appreciate your work
subscribed with Bell icon on 😊😁👍
Thanks a lot!!!
i was able to solve just by seeing the question, thank you for your help in previous videos
These series for calculus so a million times better than my college professor's. Why I'm not seeing this earlier?
Love the Lectures!! Please make a playlist on complex analysis
I plan to!
Awesome explanation..thank you.
This videos are soooooo underrated
Wow you made it look so easy :)
Great videos . Greatly appreciated. 👏
Glad you enjoyed!
Thank you sir 🔥🙏🔥
For clarity, I would have liked to have seen:
Step 1: Parameterize C
r(t) = g(t) i + h(t) j = 2 cos t i + 2 sin t j
f(x, y) = f(g(t), h(t))
But Dr. Bazett is far more clear than the old text books I consulted for review.
You do indeed teach amazing but i didnt understand a lot
maybe because i just started it
So, did we calculate the given area of the curve in this example? Anyway, thanks for the video. It really helps!
Thank you very much for your videos!
Good Explanation. I think it should be emphasized that circle at the bottom is a projection of the f(x,y).
Can I ask , how did you get (1+sin 2t) and how you get sqrt((-2sin t)^2 + (2 cos t)^2) become 2 dt ? Sorry I'm a new learner.
There is an important identity in trigonometry which is really important for these problems, its sin^2(x)+cos^2(x) = 1 for any value of x. So that’s why it’s just 1 for the 1+sin2t bit, and then you have sqrt(4sin^2(t)+4cos^2(t)) you can factor out the 4, and then the identity brings the sin^2+cos^2 to 1, so you have sqrt(4(1))=2
Also the sin2t came from the double angle formula. It says that sin(2t)=2cos(t)sin(t) hope that makes sens😊
@@ed8620is this true because the sum of these values rooted is equal to the hypotenuse in the unit circle. Which is by definition 1?
AMAZING.
Thank you!
thank you
Excellent💯💯
Good video.
Thank you man....
thanks!
lovely stuff. I am planning to take an aerodynamics course so i need some recap on math. You say in your first video that this is about 1/3 of your university course. When you say 1/3 are you referring to how many subjects you "touch" or how deep you go into each subject ? In any case i will surely be watching all the series. Thanks in advance.
Man why didn't I find your channel a little earlier?
Please do 1 video for optimization with line integrals like if we are given a multivariabe function f(x,y) and we have to compute its line integral from (a,b) to (c,d) then what should be the equation of the curve (over which the function is to be integrated) so that the line integral is minimum.
Should show how you got the parametric equations.
The line integral gives you the area under the f(x,y) and above the r(t) functions or the length of the line of the f(x,y) function that lives above the r(t) function?
hey nice video....I have a question though why when finding the height..that is the z component do you use f(x,y) instead of computing k directly..please reply ASAP
Amazing :)
Thanks! 😄
One of the topics dealt with blindly before but never visualized or understood. So line integral computes a surface area of a function over a curve, is it right?
That is one geometric interpretation yes, but there are several
WOOOOOOW !
I believe you gave the wrong g prime of t and h prime of t, it seems u just left them unprimed. or am I missing something? either way it shouldn't change the answer since it is taken as absolute in terms of distance.
oh actually I see after watching further u clarified my question cuz u wrote it right on the screen so disregard previous comment.
wow
Where it is used in high school physics
So I saw that line integrals are defined on a scalar field, is this an example of a scalar field? I haven't seen them before and am not too sure
Hi. I tried evaluating the integral at 5.12 and I'm getting 2pi as the answer. Am I doing something wrong ?!
Did you miss the orange 2 on the right?
@@DrTrefor I used U substitution on (2t) so I replaced the orange 2dt as du. The 1 integrated to 2pi and the sin(u) integrated to -cos(u) and evaluated to zero.
Ohh. I didn't distribute the 2 amongst both the 1 and the sin(2t) terms. I tagged it only with sin(2t). I get 4pi now. Thanks for replying 🙂
Hello, trying to transition to multivariable calculus. I don't really understand parameterization. Why don't we define the curve C as x^2 + y^2 = 2^2. And why are vectors being used a lot all of a sudden, unlike single-variable calculus? I hope that makes sense.
That's how the curve C is defined, indeed but to compute the line integral easily we need to parameterize it. You can watch the previous few videos in this playlist, I think they will help understand.
For your second question, it's Vector Calculus of course we're gonna be using Vectors a lot
sir why we right sometimes velocity vector as it is in line integration and some times magnitude of velocity vector?
It just depends on whether we care about speed (thus take magnitude) or velocity, and thus want direction as well.
Ez