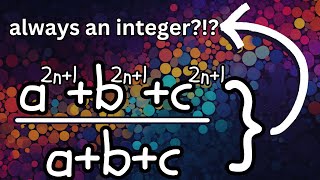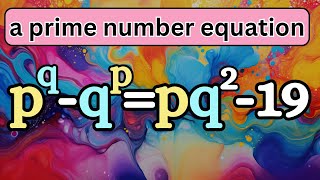You should know this number theory result -- Bertrand's Postulate
ฝัง
- เผยแพร่เมื่อ 6 ก.พ. 2025
- 🌟Support the channel🌟
Patreon: / michaelpennmath
Merch: teespring.com/...
My amazon shop: www.amazon.com...
🟢 Discord: / discord
🌟my other channels🌟
Course videos: / @mathmajor
non-math podcast: / @thepennpavpodcast7878
🌟My Links🌟
Personal Website: www.michael-pen...
Instagram: / melp2718
Randolph College Math: www.randolphcol...
Research Gate profile: www.researchga...
Google Scholar profile: scholar.google...
🌟How I make Thumbnails🌟
Canva: partner.canva....
Color Pallet: coolors.co/?re...
🌟Suggest a problem🌟
forms.gle/ea7P...