MONSTER INTEGRAL

Here's an absolutely ridiculous integral characterized by a couple of parameters. Solution development using Feynman's trick and some introductory knowledge of special functions.
My complex analysis lectures:
• Complex Analysis Lectures
If you like the videos and would like to support the channel:
/ maths505
You can follow me on Instagram for write ups that come in handy for my videos and DM me in case you need math help:
...
My LinkedIn:
/ kamaal-mirza-86b380252
Advanced MathWear:
my-store-ef6c0...

[@farfa2937]

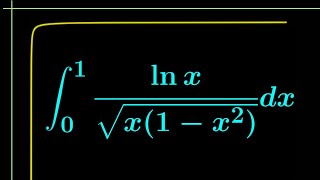
Today's integral is sponsored by an existencial crisis

[@Akhulud]

the integrals are your friends

[@thomasblackwell9507]

Yes, you have friends!

[@maths_505]

Yes my friend that intro was just for comedic relief 😂 lovely hearing from you once again. We haven't spoken on Instagram in quite a while, is everything okay?

[@kavimahajan8412]

Being early on a maths 505 video, there’s nothing greater

[@MrWael1970]

Thanks for your featured effort.

[@beautyofmath6821]

Wonderful integral

[@Patrickoliveirajf]

You are my friend ❤

[@polpotify]

In my language, Kamaal means Maximum, so you are the roof function of all Maths TH-camrs 😅

[@maths_505]

It has a similar meaning in Arabic 😂 thanks bro

[@trelosyiaellinika]

Kamaal كمال in Arabic means perfection (it may also mean completion and by extension, be interpreted as maximum in some languages that have borrowed from Arabic). I have no idea what nationality you belong to, but, in any case, the name Perfection suits you well! The evidence is in your videos! And, never let it cross your mind that you lack friends. You have a huge community of math lovers who appreciate you and wish you well.

[@aravindakannank.s.]

why u need friends when u got bros (us daily viewers)😊

[@maths_505]

SUIIIIIIIIIIIIIIIIII

[@abdulllllahhh]

I had to put aside the time that I’d spend with my (not |R) friends to watch this video

[@rv178]

Dont worry bro, every single positive integer is your personal friend

[@kavimahajan8412]

How do you figure out how to solve stuff

[@maths_505]

Well....it helps when I invent the problem in the first place 😂😂😂

[@MatthisDayer]

11:37 i suspect a phi will show up

[@MatthisDayer]

i was right

[@mikefischbein3230]

You differentiate with respect and integrate with zeal.

[@CloneAtWork]

Here's a kinda cool Integral of a double sum, maybe you like it :3 (Also F for friends)
Integral from 0 to 1 of (Sum from n=1 to inf of x^n * (Sum from k=1 to k=2n-1 of (-1)^(n+k) / binomial(2n,k))) dx
Answer should be 1-(pi^2 / 12)

[@maths_505]

Thanks

[@Ghaith7702]

awesome, also F

[@charlesbrook746]

Before using the digamma you could just factorise the numerator and have a simple polynomial integral

[@gamermessi1375]

Can you evaluate this sum:
Sum of cos(bln(x))/x^a with x going from 1 to infinity .
a and b are like parametres

[@zatsun2733]

I just have a question about the derivative regarding s of the integral;
you seem to do it freely but shouldn't we first check for continuity definition and domination of the integrated function ?

[@shivanshnigam4015]

Heres a fun series problem
Summation cos(2nx)/(4n²-1) from n= 1 to n--> infinity
Ans is (1/2)-(π/4)sinx

[@shivanshnigam4015]

@aniruddhkabra9430 😆

[@yoav613]

Noice,now give us nice integral with the trigamma function.😊💯

[@rudransh118]

respect brother F

[@shivanshnigam4015]

The actual fact is that you have friends but none of them are math nerds like you

[@MohamedachrafKadim-jm5yr]

I solve this hhh😂

[@giuseppemalaguti435]

I'(s)=I(0-->1)=(x^s-1)(1-x)/(1-x^k)...semplifico I'(s)=I(0->1) (x^s-1)/(1+x+x^2+...x^(k-1)..

[@fredfred9847]

F

[@edmundwoolliams1240]

Surely you're joking?!

[@xdShaty]

F

[@Ijkbeauty]

F