A quadratic floor equation.
ฝัง
- เผยแพร่เมื่อ 7 ก.พ. 2025
- We solve a nice quadratic equation involving the floor function.
Please Subscribe: www.youtube.co...
Merch: teespring.com/...
Personal Website: www.michael-pen...
Randolph College Math: www.randolphcol...
Randolph College Math and Science on Facebook: / randolph.science
Research Gate profile: www.researchga...
Google Scholar profile: scholar.google...
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
brave.com/sdp793
Buy textbooks here and help me out: amzn.to/31Bj9ye
Buy an amazon gift card and help me out: amzn.to/2PComAf
Books I like:
Abstract Algebra:
Judson(online): abstract.ups.edu/
Judson(print): amzn.to/2Xg92wD
Dummit and Foote: amzn.to/2zYOrok
Gallian: amzn.to/2zg4YEo
Artin: amzn.to/2LQ8l7C
Differential Forms:
Bachman: amzn.to/2z9wljH
Number Theory:
Crisman(online): math.gordon.edu...
Strayer: amzn.to/3bXwLah
Andrews: amzn.to/2zWlOZ0
Analysis:
Abbot: amzn.to/3cwYtuF
How to think about Analysis: amzn.to/2AIhwVm
Calculus:
OpenStax(online): openstax.org/s...
OpenStax Vol 1: amzn.to/2zlreN8
OpenStax Vol 2: amzn.to/2TtwoxH
OpenStax Vol 3: amzn.to/3bPJ3Bn
My Filming Equipment:
Camera: amzn.to/3kx2JzE
Lense: amzn.to/2PFxPXA
Audio Recorder: amzn.to/2XLzkaZ
Microphones: amzn.to/3fJED0T
Lights: amzn.to/2XHxRT0
White Chalk: amzn.to/3ipu3Oh
Color Chalk: amzn.to/2XL6eIJ


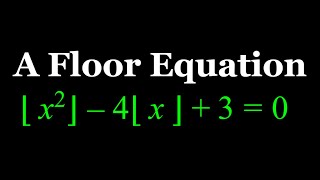






This is getting out of hand. Now there are two of them.
mitosis
He just applied Banach-Tarski on himself for a while.
Nute Gunray reacted.
13:22
That double Michael at the beginning though 😂
Just wanted to know, do you even watch the entire video before commenting?
Arsh Shankar Verma Usually, I go straight to the end for the timestamp, then I watch the entire video to see if there’s something else funny then I watch with my real account to increase TH-cam engagement.
Wow! You are a real champion for the cause!!
Good place to start 0:00
@@MichaelPennMathwhy use 1/2..i see no reason to so isn't that arbitrary?
7:46 - 7:48 : missed opportunity for Micheal #2 to come and clean the board 😁
This is genius and warrants some consideration
I like the way SyberMath solves equations with the floor function.
The equality is true when floor(xx + 1) = n = floor(2x), where n is some integer.
So the equality can only be true when both sides of the equation are equal to "n." Which gives you four nice inequalities that must be true for any solution
n
This is such a nice pace, perfectly understandable and still not monotonous. Not a lot of teachers can do that.
I guess Micheal doesnt read these comments since he never comments on some really good ideas for simplifying the proof.
My offering is to set x=n+f
n =[x]. f fraction 0
Usually TH-cam maths is way too far ahead of me but this is just close enough that I can grasp at the main concepts and learn from there. Great content mate
0:01 It's always nice when your brother Michael Nepp comes to help you with your class
Say 0:01 instead, 0:00 doesn't work
@@anshumanagrawal346 thanks, I had no idea of this lol
A more strraightforward way to see there are no solutions for x ⩾ 2:
LHS = ⌊x^2 + 1⌋ ⩾ ⌊2x + 1⌋ > ⌊2x⌋ = RHS
Right. I was thinking the same thing. Wonder why he went for that approach
idk why I was scared by seeing 2 michaels at the same time.
Nice. At the beginning I thought you'd leave us a "homework" with similar problem. I think it'd be nice))
Great suggestion!
That will be really nice for lockdown exercise
Отлично придумано.
@@IoT_ ещё бы)
@@IoT_ english plz, i don't understand Russian
I think the most intuitive way of approaching this is rejecting anything outside the interval (0,2) after solving the inequality x²+1-2x≥1. The rest is just technical.
This kind of explanation, patient with an easy example, is what I look for when I try to understand differential geometry.
floor(1+x^2)=1+ floor(x^2). floor(2x)-floor(x^2)=1 . We have so n≤2x
Nice editz 😍
Define y=x-1 and simplify to get floor(y^2+2y)=floor(2y). So y^2 has to be in the interval [0,1) and take it from there.
Did you mean floor(y^2+2y)=floor(2y+2)?
For [2, infinity)
Can't you just note that x^2 >= 2x
So floor(x^2) >= floor(2x)
Thus floor(x^2) +1 > floor(2x)
Then because integers don't affect the result of a floor of added beforehand
floor(x^2 +1) > floor(2x)
And avoid all that piece wise checking.
Excellent resolution Michael! I love this kind of exercises and I support the suggestion for you about leave us some "homework" about these. You are doing a great job!
Great to see Michael using new ideas and innovating.
I think it is easier just to start off with subintervals given by 1/2 , 1 ,root(2), 1.5, root(3) ,2 and then examine each. Thanks for all your analyses!
Some next level video you got there.
Another solution: let floor(x^2 + 1) = floor(2x) = n in Z then since x^2 + 1 >= 1, n >= 1. From the definition of the floor function n = n^2/4 so n = 1, 2, 3.
case 1: n = 1 we have 1/2
1:41
For "Our" Solution
USSR anthem playing at the back
I love this channel! Always nice to start my day off with a little math
Especially when the other side of the equation is linear (well, at least inside flooring), drawing a picture would easily give quite nice intuition on what values we are actually trying to dig out.
Finally we get another double Michael
im gaining an interest in these floor function equations. i used this as a guide to find the solutions to floor(x^2) - floor(x) - 1 = 0. desmos actually gets it wrong and has sqrt(3) as a solution when it's not
This channel is becoming more entertaining. Keep it up 👍🏼
It seems to be pretty easy to find answers, when you approach it from the graphical side, because both sides are not do hard to draw on the cords system.
compi did it too very neatly:
*Reduce[Floor[x^2 + 1] == Floor[2 x], x, Reals]*
The floor function is what I'm more familiar with, the truncation that happens in computer science. When you typecast a real number to an integer, it discards the part after the decimal, so 2.9 becomes 2, 3.01 becomes 3 and so on. Having said that, I went through a fair bit less work than Michael did to come up with the correct answer. He does have a typo on the board near the end where he includes √3 when of course it should be excluded in the final answer. To wit, you end up with these expressions:
2x ≥ 1 .... x ≥ 0.5
x² + 1 < 3 .... x < √2
2x ≥ 3 .... x >= 1.5
x² + 1 < 4 ..... x < √3
Combining these four inequalities you get
x = [0.5,√2) OR x = [1.5,√3)
@@angelmendez-rivera351 I guess I got the right answer because it didn't involve any negative numbers.
Michael has just showed the properties of a quantum particle. He can present at more than one place at a time with different states. Amazed!!!!!
This edit is so cool
By the definition of floor there exists an n in Z such that
n = 1, which is a contradiction.
If x = 0 then n
There is an easy way to see that the only solutions are in the interval (0,2). Using that a-1
What seemed more intuitive to me was to look at possible values that the two floor functions could take - I.e. 1,2,3,4, etc. for each value you can calculate a range of x values that would give that answer. The overlap in ranges for x of both functions are your solutions
i feel like there's an easier and more intuitive "approximation" of the solution. note that if floor(x) = floor(y), then abs(x - y) < 1, because floor(x) ≤ x, y < floor(x) + 1. from this abs inequality we get that x \in (0, 2), therefore floor(2x) takes only the values of {0, 1, 2, 3}. then you get 4 pretty easy cases that are almost identical to your second half of the solution and make more sense to a person who's less skilled when it comes to algebra.
Solved this in a couple of minutes by just plotting the two functions by hand, they are simple enough.
Oh so you found out exact ranges by hand
@@ushasingh6204 it's not too bad to see where the bounds should be approximately and then it's also not hard to check where exactly those bounds have to be
@@angelmendez-rivera351 graphing results more or less in a kind of guess-and-check method. it requires more guessing, but should be slightly easier to check, even though the full solution is also not too bad here
There's nothing inaccurate in doing this by graphing. Once you take the floor functions the two graphs are completely predictable, and the values where the y coordinates change are straightforward (at worst square roots of whole numbers).
Ah, so that's how you manage to output so many videos.
There's an entire army.
My man got his clones slaving away in the corner of the screen
my approach to case 2 was a little different. If x^2+1 is at least 1 more than 2x, then the floor of x^2+1 must be bigger than the floor of 2x:
x^2+1>=2x+1=>flr(x^2+1)>=flr(2x+1)=flr(2x)+1 => flr(x^2+1)>flr(2x)
also x^2+1-2x>=1 (x-1)^2>=1 =1 x>=2
Aww, I got a post on my birthday. How thoughtful of Michael.
The editing is fun, I approve
If floor(f)=floor(g) then f-g should lay in -1 to 1 so x is on 0 to 2 and if u break it to 1/2 width intervals u good to go
Excellent
Loved the intro
I graphed by hand the two equations (that's not so difficult) and i easily found solutions in a couple of minutes
Ohh..So good ,I like this solution.
Isn't it always the case that Floor[f(x)] = Floor[g(x)] implies |f(x) -g(x)|
I have to admit, I did SOME of the work to get to the solution, but then I started hunting an pecking to check values and totally missed that the the interval [sqrt(2), 1.5) is NOT a solution. That'll teach me 😂
Before watching: find the points where the two sides change value:
x, [x²+1], [2x]:
0 if n ≥ 3, so no more solns.
So: [½, √2) U [1½, √3).
That was a bit of casework, but I liked it. Suprisingly numerous number of cases for such a simple problem.
You must hire the second Michael for next videos
This is an example where itmakes sense to use excel first to get an idea. That way you see the various steps coming much easier
I'm guessing if this is a math contest problem, you wouldn't have access to electronic aids such as that.
Guys I've already seen that kind of problems, it's as easy as Michael call other Michael for other universe to help him. In Rick and Morty explain this kind of things
Cases 1 and 2 are unenlightening as it gets. This is how you solve when you know the solution beforehand. Rather, by the definition of the floor function, we have:
(1) [2x] = [x^2+1]
I solved it☺️😆. Same method almost. I proved no solutions for anything other than 0 to 2 then just checked everything like u did.😁
I feel like your solution took like 10x longer than graphing it.
floor(2x) is going to be 0 from x = [0,0.5), 1 from x = [0.5,1), 2 from x = [1,1.5), 3 from x = [1.5,2), 4 or more from x = [2,infinity)
floor(1 + x^2) is going to be 1 from x = [0,1), 2 from x = [1,sqrt(2)), 3 from [sqrt(2),sqrt(3)), 4 from [sqrt(3),2)
and they line up at x = [0.5,sqet(2)) and x = [1.5,sqrt(3))
I think this was a poor problem to choose, if the goal was to explore richness of floor-related algebra. This took me 3 minutes and no complex algebra. I just looked at question "What values of each function give outputs 0, 1, 2, 3...?" For f==floor(x^2+1), this is simply 0={}, 1=f[0..1), 2=f[1..sqrt(2)), 3=f[sqrt(2)..sqrt(3)), etc. For g==floor(2x), it's just 0=g[0,.5), 1=g[.5,1), 2=g[1,1.5), 3=g[1.5,2). My intent was to find a deeper pattern for the two functions , describe that pattern algebraically, then solve for solutions where the algebraic patterns were equal. But alas. No need for a pattern. My quick/mindless 0,1,2,3 solved the problem on the spot. The intersection of f() solutions and g() were clearly non-empty at 1,2, and 3, and trivial to list. Obviously f(x) was never less than 1, and obvious that for output of 4 or more, g(x) would always need higher inputs than f(x).
Interesting question.... Could arrive at the solution,
x ∈ [0.5, √2) U [1.5, √3)
what can i study now to understand it all?
Real numbers analysis
Another way to write the solution is U [n/2, sqrt(n)) for n= 1, 2, 3. Interesting.
Shorter & easier method:
Using [f(x)] = [g(x)] => | f(x) - g(x) | < 1, we get | x^2 + 1 - 2x | < 1 i.e. 0 < x < 2.
Since, 0 < x < 2 => 1 < x^2 + 1 < 5 & 0 < 2x < 4, therefore, 3 cases arise:
(I): 1 < x^2 + 1 < 2, 1
I did a graph of x*2 + 1 and then its floor function.
Then I did a graph of 2x and then its floor function.
This immediately gives the possible interval.
I think the more natural way to do this problem is actually to do it graphically, as that's where the intuition kicks in. It's clearer what you're doing that way. You don't even need desmos or another graphing calculator to do this. It's simple enough to accurately draw by hand, and then figure out what's exactly going on. Nevertheless, at the end of it, the proof would be very similar to the ideas the video presented. You'd have to go through the casework he's done. However, graphing would be the most intuitive start at the problem, and then casework feels more justified and sound.
I see you very much love floor function, but what about the ceiling function?
Interesting problem
I just start testing critical points for small values, and then when I see L.H.S.=R.H.S.+1 (without floor function), that is already a stop because LHS increases faster than RHS
The floor is lava is back again!!
oof that production value!
nice problem dude
I don’t know why. I just somehow hate floor function (ofc also ceil function)
lol it is sorta weird
The Double Helix I was referring to the intro lol
This can be done easily with graphical approach if someone knows how to draw graphs of floor of functions
Yes, but that isn't really a proof.
@@thiantromp6607 it is, if graphs intersect then they are equal...just draw the graphs... you'll understand how rigorous it is
@@user-yh6lr8wy9s you cannot draw the graphs from negative infinity to positive infinity. You do have to show that [x^2+1] grows quicker and stays above [2x] forever in both directions. Very simple and intuitive, but definitely necessary for a rigorous proof.
@@angelmendez-rivera351 what an idiot, the graphs are horizontal lines, you don't even need any apparatus to figure out where horizontal lines are intersecting
@@angelmendez-rivera351 maybe if you drew the graphs you would understand what i am talked about, it is very clear idiots like you can't think beyond these stupidly long so called proofs...
Since the 2 functions inside the floor function are pretty easy to graph, isn't it easier to just draw the graph and find the solution?
That's a solution but it's too 'forceful'
I plotted in Desmos.
Only now I understand how Nute Gunray felt in SW phantom menace lol
I must say I disliked the fact that all those very conveniently efficient intervals were taken out of a hat (cooked up beforehand). The proofs are not so fun, but proving a limited set of possible values for the floors ({1;2;3}) and then solving for x in each case felt much more in control.
Ans x= 1( no need to calculate)
Dos Michael jajajaja.
Liking floor function hmm... might be hidden affinity to programming 😉
OT but I love the dark red color of those pants
x^2-2x+1=0
(x-1)(x-1)
x=1
Floor function? More like "stair" function.
WHY CHOOSE 1 HALF ANS 2 THAT IS TOTALLY CONTRIVED..MAKES NO SENSE..PLEASE EXPLAIN
Damn the edit
Who’s that other guy?
i almost thought the guy on the left is his twin
FLOOR GANG
Wow! You got yourself a clone! Did you go to Kamino or order him online?
@Michael Penn: Not the efficient solution. So not impressive one unlike your previous. Graphically it is magic. Try.
If i had cancer and could wish for one thing, i would want prof. penn to end a video with "ok, so this is a sexy place to stop" in the same serious tone as all the other videos. OMG i would die of that instead of the cancer. Like if u agree so he can see it.
solution given here too long and a lengthy.Teacher would have used property of greatest integer function as
[K + 1] = [ K ] + 1 for a shorter solution.
What will be the floor of 0.99999999999.........∞???? I'm gonna go with 1
oof now there are two of them
Did you find a way to clone yourself lo!
wtf two michaels
Is it just me or do this guy looks like Mark Zuckerberg from the side
Shadow clone jutsu
Is him your twin?
This is a bit too tedious. By drawing the graphs of the two sides around x=1, one can easily reach the conclusion.