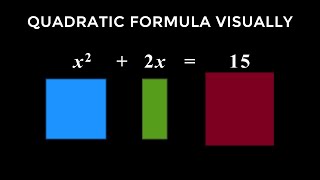
Crocodile Maths Problem That Stumped Scottish Students
ฝัง
- เผยแพร่เมื่อ 8 ต.ค. 2015
- This problem caused an uproar on social media because it was too hard, and it brought some Scottish students to tears (it gave many mathematicians crocodile tears...sorry I couldn't resist). Can you figure it out?
A crocodile preys on a zebra across the river. It swims a bit and then travels on land to catch the zebra quickly. What is the shortest time?
Watch the video to see the answers. The final part shows an elegant solution that involves physics and optics.
Clever solution by "completing the square"
www.convex.org/the-crocodile-p...
Source of story
www.bbc.com/news/uk-scotland-3...
The exam (see question 8 on page 16. I have slightly re-worded the problem for this video)
www.sqa.org.uk/pastpapers/pape...
My blog post summary (text and images): mindyourdecisions.com/blog/201...
If you like my videos, you can support me at Patreon: / mindyourdecisions
Connect on social media. I update each site when I have a new video or blog post, so you can follow me on whichever method is most convenient for you.
My Blog: mindyourdecisions.com/blog/
Twitter: / preshtalwalkar
Facebook: / 168446714965
Google+: plus.google.com/1083366085665...
Pinterest: / preshtalwalkar
Tumblr: / preshtalwalkar
Instagram: / preshtalwalkar
Patreon: / mindyourdecisions
Newsletter (sent about 2 times a year): eepurl.com/KvS0r
My Books
"The Joy of Game Theory" shows how you can use math to out-think your competition. (rated 4/5 stars on 23 reviews) www.amazon.com/gp/product/150...
"The Irrationality Illusion: How To Make Smart Decisions And Overcome Bias" is a handbook that explains the many ways we are biased about decision-making and offers techniques to make smart decisions. (rated 5/5 stars on 1 review) www.amazon.com/gp/product/152...
"Math Puzzles Volume 1" features classic brain teasers and riddles with complete solutions for problems in counting, geometry, probability, and game theory. Volume 1 is rated 4.5/5 stars on 11 reviews. www.amazon.com/gp/product/151...
"Math Puzzles Volume 2" is a sequel book with more great problems. www.amazon.com/gp/product/151...
"Math Puzzles Volume 3" is the third in the series. www.amazon.com/gp/product/151...
"40 Paradoxes in Logic, Probability, and Game Theory" contains thought-provoking and counter-intuitive results. (rated 4.9/5 stars on 7 reviews) www.amazon.com/gp/product/151...
"The Best Mental Math Tricks" teaches how you can look like a math genius by solving problems in your head (rated 4.7/5 stars on 3 reviews) www.amazon.com/gp/product/150...
"Multiply Numbers By Drawing Lines" This book is a reference guide for my video that has over 1 million views on a geometric method to multiply numbers. (rated 5/5 stars on 1 review) www.amazon.com/gp/product/150... - วิทยาศาสตร์และเทคโนโลยี








I honestly can't figure out why the students thought this problem was so hard. It's straight application of calculus 101.
But your solution using Snell's law is beautiful, congratulations!
+Bernardo Powaga I should mention the actual exam working was different, and that was probably one difficulty. I also read the entire exam was hard, so I bet there was mental fatigue that made this seem harder too.
+Bernardo Powaga Yeah, I never really got why kids would go on social media an publicly announce that they were not only incapable of answering a particular question but also found it unduly hard. Whether it's maths questions such as this or French students who claim that the word "to cope" is one only known by native speakers of the language, these people are not only bound to opening themselves to ridicule, they also conserve their teenage stupidity and attitude for every future potential employer to see. That's ... just not very smart.
+Bernardo Powaga They were Scottish students, not regular students!
+MindYourDecisions I've read the entire exam and didn't find anything particularly difficult there. On the other hand, an hour and a half to complete this second part I believe is not enough for students.
Calculus 101 is University.
This is a high school exam.
Tensor transformations are easy if you have been taught it
I sat this exam. The reason there was such a strong reaction to this exam was that the Scottish curriculum underwent a reform and this was the first year that students were taking this new course. Teachers were poorly informed about the kind of changes that were made to the structure of the exam and taught the course based mainly on the old format. The past papers at this level (before the curriculum change) were all of a very different format as well. For example, we learned a small amount of calculus but the exams never asked more involved problems such as this so all the practice and expectation anyone had didn't go beyond "differentiate the following equation". There were other problems on this paper which were quite different from what we'd been prepared for and this was towards the end and peoples university applications depended on this grade hence why it had people crying.
Thanks for the explanation. Reminds me of a computer programming course I taught in a private high school, and the students felt my final exam was unfair (first time the course was taught). A team reviewed my exam, and judged how fair or unfair it was - it was deemed largely fair.
I did it with calculus, but I like the trigonometrical/physics alternative. Either way this is a FANTASTIC problem which really tests whether students have understood what they are doing with maths. Reverse engineering by looking at an equation and deducing what the varies parts represent is such cool stuff.
Since when do crocodiles travel on land faster than they swim?
+Lloyd Grubham
Quite right too: they don't.
Featuring (for example) a wolf rather than a crocodile would have made the question seem more authentic.
+Lloyd Grubham The zebra is upstream so the crocodile would be battling a current. :-)
IamGilgamesh666
No, that's not right.
If the current were significant, then the crocodile's speed in the water (relative to land) would vary as a function of its heading, relative to the direction of current. However, the crocodile's speed in water (relative to land) is stated as a constant.
There is no current. .
+Jack Sainthill Haha, that's a valid point.
IamGilgamesh666
Thanks. :)
I think that the difficulty of this problem does not lie in the math, but in the unfortunate wording of the question.
I was asking myself two questions:
1) Since the zebra is upstream, how do you calculate the speed of the river?
2) T is the time taken for what? To cross the river? To reach the zebra? To compensate for the river’s drift?
In this case, the speed of the river is negligible. It's a slow portion of the river, where it might as well be a lake. T is the time taken to get from the crocodile's origin, to the position of the zebra. The zebra is assumed to remain stationary.
I was able to work out the answers but I didn't even think to use Snell's Law. Physics brain! You let me down! :)
+Adam Batten Nicely done. I like Snell's law because I think there's less room for calculation error. I did the chain rule incorrectly the first time and also messed up a few plus and minus signs.
@@MindYourDecisions I can see why if it is a Calculus problem, that they probably wouldn't accept Snell's law solutions. It is a coincidence that Snell's law gets you the optimal solution, as Snell's law was not originally set up such that it has to be the optimal path between two points. It is derived from the constraint of parallel wavefront continuity as wavelength is compromised to accommodate a changing wave speed. Fermat determined that it turned out to be the path of least time.
In a Calculus class teaching the fundamentals of solving optimization problems, they would want to see that you know how to solve such problems outside the context of existing shortcuts already being derived for you.
2:50 For the croc to travel straight across the river, he will actually have to swim at an angle upstream. That angle will depend on the speed of the current.
The current of the river is assumed to be negligible, since it wasn't specified.
How was this hard? It is trivial calculus. The solution was essentially spoonfed to them, by providing the formula for T(x) already, instead of merely give the speed of the crocodile on land and water.
I have a question, because I didn't do all of this stuff in school yet. At 3:14 , what does he mean by the "chain rule"?
Niko Gruben
Look up all the rules of differentiation and memorise them. Then you can do any derivative.
@@nikogruben9573 Let f be a function of y and y be a function of x. The derivative of f(y) is then f'(y) * y'(x). The ' is read as prime and means derivative.
What's incredible is how easily crocodiles get this problem right every time.
I showed this problem to my 5-year-old son so he could see some math in action. He likes math. We might all learn something from him: "It would be better for the crocodile to run the land part first and then swim across the river to surprise the zebra from the water." It's the same time and crossing angle, but further down.
Now that I realize the croc will eat the zebra, I'm crying, too. Thanks, Presh!
Presh Talwalker, your videos are the most amazing resources for Math and scientific enlightenment!!! Keep up the good job!!!
I wouldn't have thought that way in 1000 years.
Elegant and beautiful in every manner.
I had a very similar question during my high level maths exam during high school here in Denmark about 8 years ago. It was about a life guard at a beach, who had to save a person in the water by running x meters down the beach before taking different paths to the person in need. The related equation ends up exactly the same (well, different constants, but that changes nothing wrt solving the problem). Not everyone in my class got it right, but I don't think it was too bad, and none of my class mates were complaining after the exam was over...
Your solution is simply brilliant, I'm amazed by it.
It's the implication of the result that is beautiful. Students are always asking, why do I need to know this... or in another way they wonder why a word problem remotely relates to real life. His solution explains this. 3 ways:
1. It is not obvious from one run of the calculus, but is shown easily by the physics.. It DOES NOT matter where on the shoreline the zebra is (provided at least 8 m). Only the angle matters based on relative speeds. So his solution tells us more than the calculus. or at least more obviously.
2. So light doesn't just travel faster than everything else.. the route it takes is also the fastest route. So this method helps explain why light bends.
3. Cheep but true.. there is more than one way to solve a problem.
I wonder how many students got confused simply because the question didn't explicitly instruct them to assume the zebra just stands still completely unaware of the crocodile's approach.
Loved the way you solved it with Snell's Law. Keep it up!
This kind of problem is in all the textbooks about refraction. It is in the curriculum that we should try to connect different areas of physics and applications.
The mainly interesting thing concerning this problem was about the observation that overall time is made of the superimposition of two terms.
The first one addresses the time which was required to travel into water: hypotenuse of the triangle having as legs the x-distance and the river width as 6 meters.
So if one assumes the motion as uniform through a straight line the numerical coefficients represent just the reciprocal scalar velocity.
Definitely a doable exam question. Also the physics solution was nice to watch.
Solved it the first way and it wasn't really hard. Your way of solving it using physics was incredible btw.
They should have just changed the problem statement to, "Calculate the minimum upstream distance the crocodile needs to swim to achieve total internal reflection within the river." That would have cleared up any confusion.
What I like about that is that Snell's law is acquiring from Fermat's principle which pretty much ends up in calculating T(x) and taking derivative of it. We have done full circle.
I actually had a similar problem in my Physics 430 class a few years back. The question had the use of a sailboat, river-speed, air-speed, drag, and a tear in the sail.
The basic of the question was "How quickly can the Prince reach the Princess?"
It was a 5 point question that I didn't want to bother answering - so I drew a crocodile in the river and said "He can't reach the Princess, there's Crocs in the water. His quest is over."
I received partial credit.
Very nice work, especially recognising the application of Snell's Law. I mark you A+ for this test.
I would give no credit at all. It is a calc class, not physics.
I am no physicist but it seems strange to me that snell's law which is "referring to light or other waves passing through a boundary between two different isotropic media" can be applied here, This would require some thinking to be sure this is valid reasonning.
A friend of mine tried once to applied the ideal gas law to a liquid... got a well deserved F.
+Tom Tom It has to do with Fermat's least-time principle. Light travels along the path that takes the least time. Since the constraint on the allowed motion is the same (both must travel with the least time possible), we can use Snell's law, which is a consequence of the principle, in multiple applications. Crocodile or light, it doesn't matter as long as the relevant bits (the constraints) are the same; then the principle can be taken to its logical conclusion. That's the beauty of math. Liquids don't act like ideal gases so your friend was out of luck. hyperphysics.phystr.gsu.edu/hbase/phyopt/fermat.html
Exactly what Passacaglia582 has said. It doesn't matter is it light or something else, snell's law is about the road that has the least amount of time to travel. THEN, it was applied to light because, the light always chooses the way throw whitch it has the shortest amount of time to spend
Were the students taught basic calculus? If they weren't then I'm not surprised they were stumped. That's quite the logical leap to go from crocodile stalking to light refraction. If they knew calculus, then I don't see why this was terribly hard. Just follow the derivative to the result and you should be fine, no special rules were needed.
Your Snell Law solution is super elegant! "To the prosperity"
I would give 0 points to any math student that says "Oh, I'll use Snell's law!", unless he is capable of rigorously and mathematically correctly prove that the law is applicable in this particular example.
5Xum But this is like the original way Snell's law was discovered. Light always chooses the way in which it has to spend the least amount of time, which is the exactly same case like in this problem
Right Luka Popovic! Oh my God, I know you in real life...! *WOW...!!*
When I first atempted to solve this problem after the exam came out, I had a really hard time because I thought the image was in three dimensions. I wouldn't expect the animals to be lying sideways in 2D. But after getting through that, it became pretty simple
can we definitively conclude those speeds that we found by analyzing the equation or can there be other possible solutions too?
I think the problem with using Snell's Law is that Snell's Law is the solution for fastest travel time. It literally defines the fastest travel route and time values, which, in order to properly demonstrate ability, need to be deduced from a more foundational level. It's like being who the best soccer player was, and then being given the best soccer player's height, weight, and scoring stats. The point is how you get there.
You can use derivate T(x) and do a sign analysis. As a remember, derivation is definitely high school material.
Idk why students found it hard, just a basic application of derivatives.
Ahhhh! This was the final question in the SQA 2015 calculator paper in Higher Maths! I’ve done the question before (many unsuccessful attempts). Sadly, looking at the marking scheme, I don’t think using Snell’s Law would gain any marks (hats off for figuring it out this way). They were looking for you to prepare T(x) into the differentiable form, different, set to 0 and then solve for x. Optimisation skills! Really tough questions, the pass mark for this paper was 30%! The hardest higher paper SQA have released in the new higher course!
Your elegant solution is awesome :)
Dude why should a crocodile's movements obey Snell laws?
+Mohammad Shameoni Niaei Snells law itself is based on the more fundamental stationary point condition (dt/dx = 0)
+Dawar Husain I see. However that works for movements that has to external intervention. But the animal has muscles and can change it speed at any given time.
+Mohammad Shameoni Niaei Snell's Law is derived from Planck's principle of least action which is just the principle of going from point A to point B in the fastest way possible. Since part 3 is asking about the fastest possible time, that is the exact scenario that snell's law will apply to. It has to be noted, though, that snell's law ONLY applies to part 3, not to parts 1 or 2.
Ryan Wilson Thank you. Now I see.
Fennec Besixdouze Wow, not only has this been resolved, but this is one of the rudest replies I have ever seen. Not only that, but I doubt you even understand what it means to satisfy Snell's Law so don't try to pretend like you are better than he is. At least he is humble and inquisitive
Brilliant video! I thought the application of Snell's law, while valid, was somewhat roundabout and obtuse, but very creative and interesting nonetheless (although I would have to doubt that any student who could apply Snell's law would hardly struggle with the more common approach). At any rate, I remember a similar problem cropping up on Dara O'Brien's School of Hard Sums (an entertainment program on British television) a few years ago.
I don't think the solution you proposed is more elegant than the standard calculus solution. More complicated doesn't mean elegant.
It may be slightly more elegant, but it seems to require more work to get to the answer. Not sure if I'd ever use it as opposed to the first method.
I always do my math tests from scratch (no learning) and I'd figure that I would probably use the second one lol
We got a problem similar to this (man in a rowboat instead of a crocodile, but otherwise the same concept) in seventh or eighth grade, long before any exposure to calculus, trigonometry or physics. It was the first problem on a test. I looked at it for a minute and thought about calculating values of x until I found a minimum. I decided that would take too long and skipped the problem, finishing the rest of the test just before the bell rang. I got the high score in the class because no one else had chosen to skip the problem and take a zero on it. Most of them got the wrong answer anyway and the ones who completed that problem correctly had four or five unsolved problems when the bell rang.
My friend you make this 1000x harder than it needs to be
I'm confused. If the river has a current (which it obviously has, since the zebra is upstream), the shortest distance by water is when the crocodile swims directly across the river, which would make it land downstream. So the shortest distance should be with x < 0. Swimming perpendicular to the flow might be the shortest distance by air, but not by water, since the water is moving.
I had this type of questions in calculus in highschol and college and nobody cried....BUT...the physics explanation is great.
I disagree with snells law. There is no reason that it has to hold true in this case. The numbers just luckily worked out. Snells law is a constraint on light. You could make the alligator land speed anything without changing the geometry.
My problem was the following: In the graphic, it is clearly visible that the zebra is 20 meters away but on the other side of the river. That means, the crocodile doesn't have to swim only 20m, but more, since there is also the breadth of the river (the line also goes diagonal, whereas the line that says 20m only goes to the left). I think most students who had a problem with that question assumed ( as I did) that there was some clever trick to calculate this that they overlooked.
The first thing I wanted to know was how fast the river was flowing, and in what direction.
It’s optimisation. All you have to do is differentiate and solve for x
Snell's law hit me when you said it travelled at different speeds in the land and water. But the problem wasn't that difficult, you just had to mildly think on part 3.
As soon as I saw this problem... My thought was light refraction 😂 and Snell's law but I was hesitant because of the formula and the weird angles (forgot critical angle 😝)
But when you broke it down to distance and speed... It really clicked and I just love it
I have one issue with this problem.
What kind of juiced up crocodile can move faster on land than in water?
Well, the crocodile was swimming upstream to get to the zebra. That _might_ make it faster to walk.
3Blue1Brown made an interesting video on Snell's law.
The answer is very simple.
The zebra uses its magical mind powers (its not like zebras exist or anything) to make the river disappear, causing the crocodile to run away, since the quicker route would be to travel to the zebra by car, going around the world to get to the zebra. Unfortunately the crocodile dies in a car accident.
What if it does he helicopter with its tail and travels above the Zebra and then grabs it to subsequently take it into its lair?
Good point, but you forgot to consider that the sun is purple when bees walk to the hospital
beauty!! thanks for this wonderful vid.. i loved how you solved part 3
I loved the solution and u made my love for math greater!!!! ❤❤❤😍😍😍😍
One thing has been overlooked, i think: the 'zebra is upstream', indicating there is a current, from zebra towards croc. That means, even if the croc would want to end up straight across, he would have to swim at a certain angle upstream, to end at the direct opposite spot. Secondly, if he wanted to reach the exact spot of the zebra swimming, he would have to aim for a spot beyond the zebra. I.e. Do the whole maths again for all three questions. Too difficult for me by the way.
I did the first two parts easily, but I haven't done calculus yet, so in the last part I understood that in the two parts of the equation, one must increase as the other decreases, so I thought that if I made them equal each other that x would probably equal something close to what the question wanted and it worked out and I got the right answer.
The Croc isn't "upstream" if his "water speed" is a constant 1/5 b/c unless this croc is not effected by currents.
What kind of dumbass crocodile is faster on the land than in the water. This question confused me for like 5 minutes because of that. They obviously mixed up the speed modifiers.
The correct answer is that point P(rey) is at x=20, and T=83.52. The crocodile swims in a straight line because it's faster in the water and it knows it.
If you use the formula with x = 20 meters, the T = 10*sqrt(109) tenths of a second, or sqrt(109) seconds, or about 10.44 seconds.
This problem has its swim speed at 2 m/s, 7.2 KPH, or 4.47 MPH, and its sprint speed at 2.5 m/s, 9 KPH, or 5.59 MPH.
Many crocodiles have been clocked at 6-7 MPH, 9.7-11.3 KPH, or 2.7-3.1 m/s. The fastest is 10.56 MPH, 17 KPH, or about 4.7 m/s. Of course, this is a short sprint, as these animals cannot sustain that for any significant distance. The swim speed is listed as 10 KPH with a high of 15 KPH. Thus, the land and water speeds are roughly the same.
Congratulations! Another very beautyful problem to exercite our minds. I just think that the angle tetatwo must be mesured on the other side of the path to apply correctly Snell's Law. Of course, in this case, the mesurement is the same.
The first two were easy since it's nothing more than replacing x with the correct value. Then I followed a different route by looking at the first outcome, where the croc only travels through the water, we can deduct that his speed in the water is distance travelled divided by time it took so √436 meters in 5*√436*(1/10) seconds. This gives a speed of √436/(5/10*√436)=1/(1/2)=2 m/s. You can then use that in combination with the second outcome to determine the croc's speed on land. He swims 6 meters so at 2 m/s that takes him 3 seconds. The total journey takes him 110/10 seconds so on land he took (110/10)-3=11-3=8 seconds.His land speed is then 20 meters in 8 seconds so 20/8=2,5 m/s. So his respective speeds are 2 m/s in the water and 2,5 m/s on land. I think you made a mistake when calculating the speeds, the factors 5 and 4 are in 1/10 s/m so you should have multiplied by 10.
4:30: the speed is 1/4 meters per TENTHS of a second. Otherwise great video!
+Ben Hambrecht Agreed, thanks for the correction.
To my mind this illustrates the one problem with the question - using tenths of a second risks confusing the candidate. I would have avoided this by changing the coefficients to 0.5 and 0.4.
I used to teach maths, and wrote some assessments for the Scottish Qualifications Authority.
I actually did know Snell's law is used for this kind of problem. The issue I had is I thought light normally can't go 90⁰ relative to the normal vector to the boundary. I have always seen this problem where the prey is not right on the shore but a few meters onto land. Besides, I also knew doing the trig once I found the ratio of angles was going to be much harder than plug and chug on a chain rule.
My interest in physics came back after watching this video
*What if the zebra also moves? How will it change the equation?*
For Part (iii), solving dT/dx = 0 gives us two possible values for x, ie. x = 8 and x = -8 . When substituted back into T(x) we obtain 98 and 162. The shorter is , of course, 98 so we accept only x = 8.
John Conway the way Scottish pupils solve it is as it a real life situation negative values can't exist
This reminds me of a similar problem I found in a math book, and it stumped me!
"One wants to draw a power line from a power station A to a farm B.
The power station A is located next to a river that is 50 meters wide and B is located on the other side of the river. The perpendicular distance from B to the river is 100 meters and B lies 150 meters downstream from A.
The cost for building the power line on land is _a_ dollars per meter and the corresponding cost on water is _b_ dollars per meter.
a) How does one draw the line in order to minimize the cost?
b) The same mathematical problem is found if one wants to determine the path that a beam of light will travel from a point in one medium to a second point in another medium. Formulate this problem and derive Snell's Law!"
The book doesn't give an answer to this problem, but it does provide some useful tips.
"The calculations will be complicated. The derivate's roots can be determined by using the Newton-Raphson formula for given values of _a_ and _b_. Perform the calculations for some values of _a_ and _b_ that you yourself decide."
The Newton-Raphson formula is a recursive formula
x: _n+1_ = x: _n_ - f(x: _n_)/D(f(x: _n_))
where you begin with a value x: _0_ that is fairly close to the root you want to find.
If Scottish students cried because of this problem, it does not say much about the Scotts.
I never heard of this Snell and while it's neat and a great real world application, if you used it in the exam you would most likely lose marks for 'not showing your working'. I expect that the derivation of Snell's law is very similar to the expected solution anyway, since you must prove it gives the minimum distance to travel.
using Snell's law and reverse engineering the question was beautiful!!
Hey. I used derivation to calculate this. Was a quick solution. But this using Snell's is genious... I am on first year of maths and physics so I know these rules. But this is soooo thinkg out of the box. Well done
A Crocodile Maths problem please. And make it snappy!
That really was out of the box thinking !!!
Path of crock was like refraction of light :P
Wait, if the first proposition says to calculate the time when the crocodile is not traveling on water, wouldnt the x distance be 20^2+d^2(shortest distance to cross)? unless the equation is based on the x speed the crocodile has.
Why make the time in tenths of seconds? Just divide by 10 to get t(x) in seconds:
t(x) = 0.5 * sqrt(6^2 + x^2) + 0.4 * (20 - x) seconds
t(x) = sqrt(x^2 + 6^2)/2 + (20 - x)/2.5 seconds
That is, the river is 6 meters wide; the crocodile swims at 2 m/s and runs at 2.5 m/s.
[It appears that the river isn't flowing, as the crocodile's swim speed is unaffected by the angle along the river at which it swims.]
(i) x = 20 meters
t(20) = sqrt(10^2 + 3^2) seconds = sqrt(109) seconds or about 10.44 seconds
(ii) x = 0 meters
t(0) = 3 + 8 seconds = 11 seconds
(iii) Find x for t'(x) = 0, and compute t(x).
t'(x) = 1/2/2/sqrt(x^2 + 6^2)*2*x - 1/2.5 = x/2/sqrt(x^2 + 6^2) - 0.4 = 0
x^2 = 0.8^2 * (x^2 + 6^2)
x^2 * (1 - 0.64) = (0.8*6)^2
x^2 = 4.8^2 / 0.36 = (4.8/0.6)^2 = 8^2
x = +/- 8, keep 8 and discard -8, so x = 8 meters
t(8) = sqrt(8^2 + 6^2)/2 + (20 - 8)/2.5 seconds = 5 + 4.8 seconds = 9.8 seconds
After I solved these problems, I watched the video. It mentions 1/5 and 1/4 meters per second. That's wrong. The unit is meters per tenth of a second. Edit: That is, 1/5/(1/10) and 1/4/(1/10) m/s becomes 2 and 2.5 m/s, respectively.
i liked the snell's law idea .. pretty amazing video 👍
I definitely prefer your solution. But the problem is entirely unrealistic. The croc would never cross the river and attack on land (assuming an able bodied zebra). It would more likely swim to a point upstream of the zebra, and, doing its best to simulate a piece of driftwood, gradually allow the distance to the unsuspecting equine to dwindle until he can ambush it in a paroxysm of tail thrashing movement.
What I want to know is how knowing the answer is going to help you get a job. Exams consist of these questions, and your ability to work in a certain field is determined by your ability to do things like this.
Beauitful solution! I m fascinated.
This is quite a basic application of calculus; they didn't even need to give you T(x).
@MindYourDecisions, Believe it or not, I was asked this question in 2011 long before it came in Scottish paper. My question is how Snell's law is acting as the shortest time finder. Please, this stills puzzles me. Kindly answer someone.
Thank you.
bc light will always take the path that takes the least time. snell's law tells you the math behind it, and if you want your crocodile to act like light then make it take the least time
I assume that the shortest distance in problem (ii) is the diagonal, which is the same answer for problem (i)
Absolutely brilliant.
I would initially say that not knowing the width of the river makes it impossible to solve, but, it is nicely hidden in that equation.
wording and explanation in this particular video is quite poor, which is weird cause Presh always provides the entire problem and solution.
the question states that the croc goes faster in water, then how is the speed in water lesser than that on land?
Great video, but I was wondering how you could conclude that the zero of the functions derivative will give the value of x where the original is at its global minima
(Sorry if that's badly worded)
But my main question is that if I gave you a function and asked what the smallest value it could possibly have is, could you simply equate it's derivative to zero and solve for x?
What about functions with multiple turning points?
+Daanyaal Sobani you cannot, the derivative returns (for T'(x) = 0) x is plus minus 8. But it has to be +8. I assume you're talking about multiple minima
Personally, I think that while the calculus minimization approach is "old hat" it is more elegant. I also am amused that this could imply the crocodile has a different wavelength depending on whether it is on land or on water.
What I wonder is how the test writers were expecting the solution to be determined. I'm guessing the calculus method. But this type of problem has been given as a "real world" analogy of Snell's law before as the drowning person and the lifeguard.
+DrRawley To be far... Since the crocodile is moving at a different velocity in water than on land, quantum mechanically it DOES have a different wavelength. Albeit there is not a very significant change...
*****
you can equate ratio of velocities to ratio of wavelength.
+DrRawley The calculus approach would have been expected. This question was in an examination paper for the Scottish Higher mathematics syllabus. There would likely have been students sitting this exam who were not also studying physics. Although the Snell's law solution is neat it would not be the preferred approach for a student sitting this exam.
AJ Johnston
I agree
Sidenote: The crocodile's velocity in a vacuum is C.
Mind-blowing, beyond imagination.
Could linear programming be used? Learnt it back in secondary school in 1975.
2:00 since when is the hypotenuse equal to the adjacent side?
What age group was this exam specified for ? Im in high school and was able to solve a majority of the problems in the exam without any issues, especially this one! Calculus problems are a staple in our schooling system
+julian hamama lol we have a badass here! X2 Sickdog Here. BTW: you should be studying fool :P
+julian hamama 15 year olds.
+julian hamama They're a staple in all schooling systems, you potato.
+Dusty Pigeon They're not, actually. Usually they're an option only for the top students in their final year of high-school. Perhaps it depends what country you are from.
I haven't heard of any first world country except the USA where you can choose not to have calculus in high school (if you go through all 12 or 13 years). Correct me if I'm wrong. Maybe times have changed?
So, how much time does the croc have to wait after eating the zebra before he goes back in the water? Mom always told me not to go swimming for at least a half hour after lunch.
Crocodiles aren't like humans. They can eat on land and in the water, and can stay in the water after eating.
This was so hard it made a student cry? Is this the new standard of hard for students nowadays?
Good catch for the application of snells law.
I don't understand the math behind your answer but just by eyeballing the lines I can tell the line you marked as 8 was shorter then the other line that was marked as 6. Is the problem with this question that the test gave the wrong length of the line marked 6 in relation to the other variables in the equation/formula that was provided?
+Stewie griffin One must never assume a diagram in a math problem is to scale.
The crocodile equation is consistent with an object governed by Snell's law. But you haven't demonstrated that the crocodile equation can be true only if Snell's Law applies.
I suspect such a thing is demonstrable without much difficulty, but without doing so, I don't think it's correct to assume that the optics approach will necessarily give the same answer as the setting-the-derivative-to-zero approach.
or you could put the graph equation in your graph-calculator and make it find the x for when the graph is at its lowest.
T is in the y-axel so then you just calculate stuff and get the righty awnser ;)
OfficialSwebent and you’d get 0 marks and your exam would be null due to using a prohibited item
Nice use of the law..
Would be a drag if the angle was something else apart from 90 though