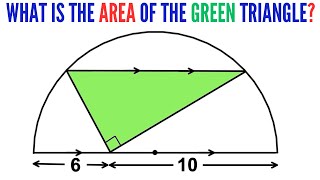
Can you find Area of the Yellow triangle? | (Two right triangles) |
ฝัง
- เผยแพร่เมื่อ 9 ก.พ. 2025
- Learn how to find the area of the Yellow triangle. Important Geometry and Algebra skills are also explained: area of the triangle formula; similar triangles; Pythagorean Theorem; right triangles. Step-by-step tutorial by PreMath.com
Today I will teach you tips and tricks to solve the given olympiad math question in a simple and easy way. Learn how to prepare for Math Olympiad fast!
Step-by-step tutorial by PreMath.com
• Can you find Area of t...
Need help with solving this Math Olympiad Question? You're in the right place!
I have over 20 years of experience teaching Mathematics at American schools, colleges, and universities. Learn more about me at
/ premath
Can you find Area of the Yellow triangle? | (Two right triangles) |#math #maths #geometry
Olympiad Mathematical Question! | Learn Tips how to solve Olympiad Question without hassle and anxiety!
#FindArea #YellowTriangleArea #SimilarTriangles #CongruentTriangles #PythagoreanTheorem #RightTriangles #Triangle #AreaOfSquare #AreaOfTriangle #CircleTheorem #GeometryMath #EquilateralTriangle #PerpendicularBisectorTheorem
#MathOlympiad #ThalesTheorem #RightTriangle #RightTriangles #CongruentTriangles
#PreMath #PreMath.com #MathOlympics #HowToThinkOutsideTheBox #ThinkOutsideTheBox #HowToThinkOutsideTheBox? #FillInTheBoxes #GeometryMath #Geometry #RightTriangles
#OlympiadMathematicalQuestion #HowToSolveOlympiadQuestion #MathOlympiadQuestion #MathOlympiadQuestions #OlympiadQuestion #Olympiad #AlgebraReview #Algebra #Mathematics #Math #Maths #MathOlympiad #HarvardAdmissionQuestion
#MathOlympiadPreparation #LearntipstosolveOlympiadMathQuestionfast #OlympiadMathematicsCompetition #MathOlympics #CollegeEntranceExam
#blackpenredpen #MathOlympiadTraining #Olympiad Question #GeometrySkills #GeometryFormulas #Angles #Height
#MathematicalOlympiad #OlympiadMathematics #CompetitiveExams #CompetitiveExam
How to solve Olympiad Mathematical Question
How to prepare for Math Olympiad
How to Solve Olympiad Question
How to Solve international math olympiad questions
international math olympiad questions and solutions
international math olympiad questions and answers
olympiad mathematics competition
blackpenredpen
Andy Math
math olympics
olympiad exam
olympiad exam sample papers
math olympiad sample questions
math olympiada
British Math Olympiad
olympics math
olympics mathematics
olympics math activities
olympics math competition
Math Olympiad Training
How to win the International Math Olympiad | Po-Shen Loh and Lex Fridman
Po-Shen Loh and Lex Fridman
Number Theory
There is a ridiculously easy way to solve this Olympiad qualifier problem
This U.S. Olympiad Coach Has a Unique Approach to Math
The Map of Mathematics
mathcounts
math at work
Pre Math
Olympiad Mathematics
Two Methods to Solve System of Exponential of Equations
Olympiad Question
Find Area of the Shaded Triangle in a Rectangle
Geometry
Geometry math
Geometry skills
Right triangles
imo
Competitive Exams
Competitive Exam
Calculate the Radius
Equilateral Triangle
Pythagorean Theorem
Area of a circle
Area of the sector
Right triangles
Radius
Circle
Quarter circle
coolmath
my maths
mathpapa
mymaths
cymath
sumdog
multiplication
ixl math
deltamath
reflex math
math genie
math way
math for fun
Subscribe Now as the ultimate shots of Math doses are on their way to fill your minds with the knowledge and wisdom once again.








It's an awesome solution from
Another awesome professor..
.....
❤ ❤
😊
Glad to hear that!
Thanks dear❤
ΔABE and ΔCDE are similar by angle-angle (
Excellent!
Thanks for sharing ❤️
Truely exciting mixture of algebra and geometry concepts. ❤
1. For single unknown x, only 1 equation is needed for its solution.
The equation is provided by the common hypotenuse of the 2 right-angled triangles using
Pythagoras theorem.
x is found to be 7.
Hence AB = 5, CD = 2, AD = 11 and BC = 10.
2. To find area of yellow triangle, area-base side ratio for equal height triangles is the obvious
method when the areas of the 2 right-angled triangles can be easily calculated. Hence knowing
AE, ED, BE, EC is crucial. 4 equations are needed to solve these 4 unknowns.
With the derived lengths of AD = 11 and BC = 10, and side ratio of similarity triangles AEB and
CED (similarity confirmed by AAA) provided by AB/CD = 5/2. Four equations can be set up:
(1) AE + ED = 11
(2) BE + EC = 10
(3) AE/CE = 5/2
(4) BE/DE = 5/2
For clarity, let AE = a, BE = b, CE = c, DE = d.
The 4 equations are:
(1) a + d = 11 (2) b + c = 10 (3) a/c = 5/2 (4) b/d = 5/2
Add (1) & (2) a + c + b + d = 21
Substitue a for c and b for d using (3) c = (2/5) a and (4) d = (2/5) b
a + (2/5)a + b + (2/5)b = 21
a + b = 15
Substitute d for b using (4) b = (5/2) d
a + (5/2)d = 15
d = (2/5)(15 - a)
From (1) d = 11 - a
Hence (11 - a) = (2/5)(15 - a)
a = 25/3
3.For equal height triangles ACE and ACD, their base side ratio AE:AD = a: 11 = (25/3):11
= their area ratio
As area of ACD = (2 x 11)/2 = 11
Hence area of ACE = [(25/3)/11] x 11 = 25/3.
Excellent!
Thanks for sharing ❤️
I got the solution with similar triangles but only after a long while, the other method is quite ugly but once you’ve gotten the value of x and the perpendicular heights of the triangles to AC, you can use coordinate geometry and find the intersection of the lines, giving you the value for the height and then find the area using bh/2. Really good problem! 👍
Excellent!
Glad to hear that!
Thanks for sharing ❤️
(x-2)²+(x+3)²=(x-5)²+(2x-3)² 2x²+2x+13=5x²-22x+34 3x²-24x+21=0
x²-8x+7=0 (x-1)(x-7)=0 x=1 is rejected , x=7
AB=5 CD=2 BE=10 AD=11
⊿ABE∞⊿CDE ⊿ABE=25s ⊿CDE=4s △AEC=x
⊿ABC=5*10/2=25 ⊿CDA=2*11/2=11
25s+x=25 4s+x=11 21s=14 s=2/3 x=25/3
x=△AEC=Yellow triangle area : 25/3
Excellent!
Thanks for sharing ❤️
Let AC=a
(x-2)^2+(x+3)^2=a^2
(2x-3)^2+(x-5)^2=a^2
x^2-4x+4+x^2+6x+9=4x^2-12x+9+x^2-10x+25
2x^2+2x+13=5x^2-22x+34
5x^2-22x+34-2x^2-2x-13=0
3x^2-24x+21=0
x^2-8x+7=0
(x-1)(x-7)=0
So x=7
area of the yellow triangle=1/2(11)(2)-1/2(2)(2.67)=8.33 square units.❤❤❤ Thanks.
Excellent!
Thanks for sharing ❤️
I began just as you did, I found x = 7 and AC = 5.sqrt(5)
Then I noticed that triangles EDC and EBA are similar (proportion 5/2). I notes a = ED, then EC = sqrt(a^2 +4) in triangle EDC
10 = BE + EC = (5/2).a + sqrt(a^2 +4) gives that a = 8/3. At that point I have every side length.
AE = 25/3, EC = 10/2 and AC = 5.sqrt(5) and I finished with the Heron formula with p = (5/6).(7 +3.sqrt(5)) the half perimeter.
I found the area of triangle AEC = 25/3. My solution is longer than yours.
Thanks for sharing ❤️
Thank you!
You are very welcome!
Thanks ❤️
(x-2)² + (x+3)² = (2x-3)² + (x-5)²
(x²-4x+4) + (x²+6x+9) = (4x²-12x+9)+(x²-10x+25)
2x² + 2x + 13 = 5x² - 22x + 34
3x² - 24x + 21 = 0
x² - 8x + 7 = 0
(x-7)(x-1) = 0
x = 7 | x = 1 ❌ AB < 0
AB = (7) - 2 = 5
BC = (7) + 3 = 10
AD = 2(7) - 3 = 11
DC = (7) - 5 = 2
CA =√(5²+10²) = √125 = 5√5
Draw EF, where F is a point on CA where EF is perpendicular to CA. By SAS, ∆EFA is similar to ∆ADC and ∆CFE is similar to ∆ABC. Let CF = y.
EF/FA = DC/AD
EF/(5√5-y) = 2/11
EF = (2/11)(5√5-y) ----[1]
FE/CF = AB/BC
FE/y = 5/10 = 1/2
FE = y/2 ----[2]
(2/11)(5√5-y) = y/2
10√5/11 - 2y/11 = y/2
10√5/11 = y/2 + 2y/11 = (11y+4y)/22
15y/22 = 10√5/11
y = (10√5/11)(22/15) = 4√5/3
FE = (4√5/3)/2 = 2√5/3
A = bh = 5√5(2√5/3)/2 = 25/3
Excellent!
Thanks for sharing ❤️
I like your method! However, as I've done in the past, I like to try the “intersecting line functions” method. It really isn't much different in terms of work.
Define a few short variables
[1.1] 𝒉 … the height of the '2' sided △
[1.2] 𝒚 … the height of the '5' sided △
[1.3] 𝒒 … the bit in from the margin of the 𝒉 vertical
[1.4] 𝒎 … the bit in from the margin of the 𝒚 vertical
[1.5] 𝒃 … the base of the whole thing
[1.6] 𝒙 … the point along 𝒃 where the two △ cross
[1.7] 𝒛 … the height of that crossing
Since it makes no difference whether one solves it 'right-side-up' or 'upside down', I chose to flip it over.
In any case,
[2.1] 𝒃 = √(125)
[2.2] 𝒃 = 5√5
[2.3] 𝒃 = 11.18
Y'all might not remember it, but worth remembering are the 'height of a right triangle internally' formulæ.
[3.1] 𝒎 = 5² / 𝒃 ... short-side * short-side divided by hypotenuse
[3.2] 𝒎 = 5 × 5 ÷ 5√5
[3.3] 𝒎 = 5 / √5
[3.4] 𝒎 = 5 × √5 / √5²
[3.5] 𝒎 = √5
[3.6] 𝒎 = 2.2361
[4.1] 𝒚 = 5 × 10 / 𝒃
[4.2] 𝒚 = 5 × 2 × 5 ÷ 5√5
[4.3] 𝒚 = 2√5
[4.4] 𝒚 = 4.4721
[5.1] 𝒒 = 2²/5√5
[5.2] 𝒒 = 4 ÷ 5√5
[5.3] 𝒒 = 0.35777
[6.1] 𝒉 = (2 × 11)/5√5
[6.2] 𝒉 = 1.9677
Then, from these, defining the linear functions of the hypotenuses
[7.1] g(𝒙) = 𝒚𝒙 / (𝒃 - 𝒎) ⊕ 0
[7.2] f(𝒙) = -𝒉𝒙 / (𝒃 - 𝒒) + ( 𝒉𝒃 / (𝒃 - 𝒒) )
Set those 2 equal to each other and determine what 𝒙 is
[8.1] 𝒙 = 2.9814 … and of course plugging into [7.1]
[8.2] g(𝒙) = 1.4907
Well, now the area is kind of obvious
[9.1] Area = ½ base height
[9.2] Area = ½ 𝒃 g(𝒙)
[9.3] Area = 8.333333 ( which is 25⁄3 )
YAY? Completely different route, but produces satisfactory results directly. Very little geometry required.
⋅-⋅-⋅ Just saying, ⋅-⋅-⋅
⋅-=≡ GoatGuy ✓ ≡=-⋅
Excellent!
Glad to hear that!
Thanks for sharing ❤️
I did it slightly differently. I solved for x and AC the same way as in the video. To get the area of ACE I used the areas of the two right trianges ABC and ADC.
The areas of the triangles follow these equations:
ABC=ABE+AEC =25 (1)
ADC=DEC+AEC=11 (2)
We note that ABE and EDC are similar triangles. Furthermore, segment DC is the side of EDC that corresponds to segment AB of triangle ABE.
We know that DC=2 and AB=5. Thus the area of triangle DEC will be the square of the ratio of these sides compared to the area of triangle ABE.
Thus, in terms of areas, DEC=(4/25)*ABE.
So we modify equation 2 to get
ADC=(4/25)*ABE+AEC = 11
or
ABE+(25/4)AEC=(25/4)*11=275/4 (2a)
Now take equation (2a)-(1)
we get (21/4)*AEC=275/4-25=275/4-100/4=175/4
thus 21*AEC=175
AEC=175/21= 25/3
Since we are dealing with two right triangles whose hypotenuse is in common, we can write the system of equation (x − 2)² + (x + 3)² = (2x − 3)² + (x − 5)² leading to 3x² − 24x + 21 = 0 and the solutions x = 1 or x = 7.
Since 2x − 3 or x − 5 would be negative with x = 1, we must discard it. So we are left with x = 7 which gives AB = 3, BC = 10, AD = 11 and CD = 2. Then AC = 5√5, sin (CAD) = 2/5√5 and sin (ACB) = 5/5√5 = 1/√5.
Now we are dealing with an ASA triangle. So the sinus of the third angle (AEC) is 3/5 and AE = 25/3 and CE = 10/3. Therefore the area of the yellow triangle is ½ (25/3) (10/3) (3/5) = 750/90 = 25/3 square units.
Thank you PreMath! 🙏
Excellent!
You are very welcome!
Thanks for sharing ❤️
Hi, thank you for this great question and answer of it. I solved it with similitary of ABE and CDE triangles after I found x by using pythagorean relation between ABC and ADC triangels. I thought it would be so easier with this method
For finding height of triangle AEC, I would like to suggest a method to avoid using similar triangles which are prone to mistakes when constructing corresponding sides proportionality equations. Let angle CAD be A and angle BCA be B and height be h.
From the found values of the sides, tanA = 2/11 and tanB = 5/10. AC = 5(sqrt 5) = h/tanA + h/tanB = 11h/2 + 10h/5 = 75h/10. Hence h = (2/3)(sqrt 5).
Thanks for sharing ❤️
One interesting question could be added: What is the length BD?
Answer: We use the Ptolemy theorem as ABCD is in the circle of diameter[A,C]: We have AD.BC = AB.CD + AC.BD. So 11.10 = 5.2 + 5.sqrt(5).BD
We have then that BD = 100/(5.sqrt(5) = 20/sqrt(5) = 4.sqrt(5).
Buenas tardes Sres. PreMath. Gracias por este interesante problema geométrico. Tengo una inquietud y necesito su valiosa opinión. Con las medidas obtenidas he construido la gráfica, pero noto que no se aprecian los ángulos rectos B y D = 90 grados. agradeciéndole la atención que se digne en prestarme. Éxitos.
Let's find the area:
.
..
...
....
.....
The triangles ABC and ACD are both right triangles, so we can apply the Pythagorean theorem for both of them:
AC² = AB² + BC² ∧ AC² = AD² + CD² ⇒ AB² + BC² = AD² + CD²
(x − 2)² + (x + 3)² = (2*x − 3)² + (x − 5)²
x² − 4*x + 4 + x² + 6*x + 9 = 4x² − 12*x + 9 + x² − 10*x + 25
0 = 3x² − 24*x + 21
0 = x² − 8*x + 7
0 = (x − 7)*(x − 1)
⇒ x = 7
∨ x = 1
For x=1 not all side lenghts are positive, so the only useful solution is:
x = 7:
AB = x − 2 = 7 − 2 = 5
AD = 2*x − 3 = 2*7 − 3 = 11
BC = x + 3 = 7 + 3 = 10
CD = x − 5 = 7 − 5 = 2
AC² = AB² + BC² = 5² + 10² = 25 + 100 = 125 ⇒ AC = √125 = 5√5
Now let's add the point F on AC such that AEF and CEF are both right triangles. In this case the triangles AEF and ACD are similar and the triangles CEF and ABC are similar as well. So we can conclude:
EF/AF = CD/AD = 2/11
EF/CF = AB/BC = 5/10 = 1/2
(EF/AF)/(EF/CF) = (2/11)/(1/2)
(EF/AF)*(CF/EF) = (2/11)*(2/1)
CF/AF = 4/11
⇒ CF = (4/11)*AF
AC = AF + CF = AF + (4/11)*AF = (15/11)*AF
⇒ AF = (11/15)*AC
⇒ EF = (2/11)*AF = (2/11)*(11/15)*AC = (2/15)*AC
Therefore the area of the yellow right triangle turns out to be:
A(ACD) = (1/2)*AC*h(AC) = (1/2)*AC*EF = (1/2)*AC*(2/15)*AC = AC²/15 = 125/15 = 25/3
Best regards from Germany
Excellent!
Thanks for sharing ❤️
No need to find AC or h.
A,B,C,D are points of a circle. So use the chord theorem to find BE (or DE) and then subtract the areas of two right triangles.
It works! Simply set the following system of equations: {ab = cd, a + b = 11, c + d = 10, 5² + c² = a² or 2² + b² = d²}.
Solutions: a = 125/7, b = −48/7, c = 120/7, d = −50/7 (rejected) or a = 28/3, b = 8/3, c = 20/3, d = 10/3 (accepted).
Thanks for sharing ❤️
Sir solve √(5-x)= 5-x^2 😊😊😊
5 − x = (5 − x²)²
5 − x = 25 − 10x² + x⁴
x⁴ − 10x² + x + 20 = 0
x = ½ (1 − √17), x = ½ (√21 − 1)
How u find the roots would u clarify
@@rakeshkumarrkk5498 Very simply: I used an equation solver... hence the mistakes in my quartic equation (now corrected) 😉
Manually, since we are dealing with a Double Multiplicity-2 (DM2) case, I would start by splitting it into (x² − x − 4) (x² + x − 5) = 0
@ 14:18 isolation of h could lead to depression and cognitive decline. ...not in this case though! 🙂
😀
Thanks ❤️
شكرا لكم على المجهودات
Pythagore 2 fois ...x=7
EAB et ECD semblables
S(EAB)=m^2S(ECD)
m=CD/AB=2/5
S(ABE)+S(ACE)=25
S(CDE)+S(ACE)=11
S(ABE)=50/3
S(ACE)=25/3
guess I'm going back to Pre PreMath
No worries! 😀
Thanks ❤️
Once x is calculated to be 7.
Tan BCA = 5/10, BCA = 26.565 degrees.
Tan DAC = 2/11, DAC = 10.305 degrees.
AC^2 = 5^2 + 10^2 = 125.
AC = 11.18.
Angle AEC = 180 - 26.565 - 10.305 degrees.
AEC = 143.13 degrees.
Sine Law.
11.18/sin143.13 = EC/sin10.305.
EC = 11.18 x sin10.305/sin143.13.
EC = 3.33.
Area yellow = 1/2 x 3.33 x 5.
8.33.
Excellent!
Thanks for sharing ❤️
I divided this Problem in two Major Parts:
A) Easy Part
B) Difficult Part
Let's go adventuring!!
A) Easy Part
1) Quest for X. X must be bigger than 2; X > 2
2) AC^2 = (X - 2)^2 + (X + 3)^2
3) AC^2 = (2X - 3)^2 + (X - 5)^2
4) AC^2 = AC^2; so:
5) (X - 2)^2 + (X + 3)^2 = (2X - 3)^2 + (X - 5)^2
6) Two Solutions : X = 1 and X = 7
7) The only Possible Solution is X = 7
8) AC^2 = 25 + 100 = 125
9) AC^2 = 121 + 4 = 125
10) AC = sqrt(125) = 5*sqrt(5)
B) Difficult Part
1) tan CAD = 2/11
2) tan ACB = 5/10 = 1/2
Using Analytic Geometry we have two Lines: Line AD and Line BC; and we want to find the Point of Interception by a System of Two Linear Equations with Two Unknowns.
3) Y = - 2X/11
4) Y = X/2 + sqrt(125)/2
5) As: Y = Y
6) - 2X/11 = X/2 + sqrt(125)/2
7) One Solution : X = - (11*sqrt(5)) / 3
9) Y = - 2X/11
10) Y = - 2 * [ - (11*sqrt(5)) / 3] / 11 ; Y = 22*sqrt(5)) / 33 ; Y = 2*sqrt(5)/3 Y ~ 1,4907
11) Base = 5*sqrt(5)
12) height = 2*sqrt(5)/3
13) Area = (Base * height) / 2
14) 2A = [5*sqrt(5)] * [2*sqrt(5)/3] ; 2A = (10*5) / 3 ; 2A = 50/3 ; A= 50/6 ; A = 25/3 ; A ~ 8,333(3)
15) So, my answer is that the Yellow Triangle Area is equal to 25/3 Square Units, or equal to approx. 8,333 Square Units.
Excellent!
Thanks for sharing ❤️
My way of solution ▶
ΔABC is a right triangle with the hypotenuse AC
ΔADC is a right triangle with the hypotenuse AC
if we write the Pythagorean theorem for ΔABC, we get:
AB= x-2
BC= x+3
AB²+BC²= CA²
(x-2)²+(x+3)²= CA²
if we write the Pythagorean theorem for ΔADC, we get:
AD= 2x-3
DC= x-5
AD²+DC²= CA²
(2x-3)²+(x-5)²= CA²
while CA² is same in both eqautions:
(x-2)²+(x+3)²= (2x-3)²+(x-5)²
x²-4x+4+x²+6x+9= 4x²-12x+9+x²-10x+25
2x²+2x+13= 5x²-22x+34
3x²-24x+21=0
divided by 3 we get:
x²-8x+7=0
Δ= 64-4*1+7
Δ= 64-28
Δ= 36
√Δ= 6
x₁= (8+6)/2
x₁= 7
x₂= (8-6)/2
x₂= 1
AB= x-2
if we put x= 1
AB= -1 < 0 ❗
⇒
x= 7
AB= 5
BC= 10
AD= 11
DC= 2
∠(BEA)= ∠(DEC) = α
if α+ β= 90°
∠(EAB)= ∠ (ECD)= β
so, ΔABE ~ ΔCDE both triangles are similar:
BE/ED = EA/CE= AB/DC
AD= 11
EA=y
ED= 11-y
BC= 10
BE= z
CE= 10-z
⇒
z/11-y= 5/2= y/10-z
2y= 50-5z
2y+5z=50
2z= 55-5y
5y+2z= 55
10y+25z= 250
-10y-4z= -110
21z= 140
z= 140/21
z= 20/3
y= 25/3
Ayellow= A(ΔABC) - A(ΔABE)
Ayellow= (AB*BC)/2 - (AB*BE)/2´
Ayellow= (5*10)/2 - (5*20/3)/2
Ayellow= 25- (50/3)
Ayellow= 25/3 square units ✔
legal, sistema.