วีดีโอ

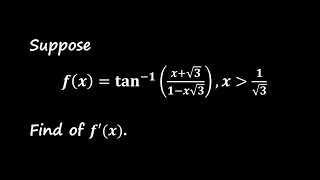
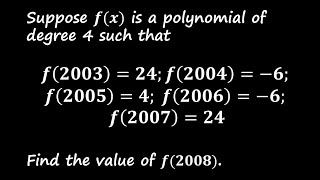
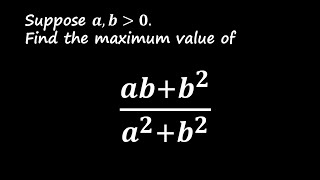
Good problem and its solutions

cool

this can also be solved by using lagrangian multiplier and find the minimum value of (x-8)²+(y-15)² subject to the constraint x²+y²=49 or 7, and we find that x²+y² =49 gives a min value of 100

One small typo: At 8:25, the x values are 25/24*[2 +- sqrt(3)], not 25/24*[4 +- sqrt(3)]. This did not affect the difference between the x values later on, so the area calculation came out correct.

Thanks for sharing!

a + ab + abc = 1997 a(1 + b + bc) = 1997 a(1 + b(1 + c)) = 1997 1997 is prime, so either a = 1 or a = 1997 if a = 1997 1 + b(1 + c) = 1 b + bc = 0, which is rejected because b and c are positive integers a = 1 in all solutions 1 + b(1 + c) = 1997 b(1 + c) = 1996 1996 = 2^2 * 499 so b = 1, 1+c = 1996, c = 1995 b = 2, 1+c = 998, c = 997 b = 4, 1+c = 499, c = 498 b = 499, 1+c = 4, c = 3 b = 998, 1+c = 2, c = 1 reject b=1996 because 1+c = 1 and c = 0, c must be a positive integer final solutions (1, 1, 1995) (1, 2, 997) (1, 4, 498) (1, 499, 3) (1, 998, 1)

Show how you check that 1997 is a prime number. Similarly, show how you check that 499 is a prime number. If you know this, the task is trivial. When trying to solve it, I suspected that 1997 was a prime number, but I didn't want to waste my time checking. Show how you can quickly check this (without a calculator).

How are we supposed to know which numbers are prime, though?

Good problem on Number System .

9 is the highest number in this realm no matter how high you count number of completion 1089 and 6174 both add up to equal 9 the only way to excede the number 9 is through physical death or earthly transition i dont know how i know this seriously

Solved it, thanks!

Thank you. For p>=3,odd prime,p^4 is odd number p^4+31 is even greater than 31 If p is prime p^4+31 is also prime. (2,47) This is only addition.

Nice! Thanks for sharing!

Sorry for the following typo errors: 1:33 we consider the quadratic equation (in u), so we shoule write u>0 and u is real. 5:00 equality holds iff (a,b)=((sqrt(2)-1)t ,t) for positive t.

A trig substitution would work pretty well: a = r*cos t, b = r*sin t for 0<r and 0<t<pi/2. The denominator cancels out to give J = (sin t)(cos t) + (sin t)^2, which can be simplified with double angle and angle addition formulas. J = 1/2*[ 1 + sin(2t) - cos(2t) ] = 1/2*[ 1 + sqrt(2) * (sqrt(2)/2*sin(2t) - sqrt(2)/2*cos(2t)) ] = 1/2*[ 1 + sqrt(2) * (cos(pi/4)*sin(2t) - sin(pi/4)*cos(2t)) ] = 1/2*[ 1 + sqrt(2)*sin (2t - pi/4) ] <= 1/2*[ 1 + sqrt(2) ] Equality would be when 2t= 3pi/4, so sin(2t) = sqrt(2)/2 and cos(2t) = -sqrt(2)/2.

Nice, but there's no need to include AI-generated videos of a person. Serves no useful purpose.

Nice solutions! Thanks for sharing!

Clever trick! Nice solution 💯! Thanks for sharing!

Interesting problem and its solution ❤❤❤

Always a pleasure to see the problems you post. Thanks for sharing.

Nice solution! Thanks for sharing!

Good problem and its solution

Nice approach.

Smart solution! Thanks for sharing!

Double cauchy is genius

For 3 digit, u minus large with small becomes 495

Am-gm by balancing powers without substitution works too

Thank you so much 😮 😊😊😊😊

Amazing solution! Thanks for sharing!

Nice!!

Hello sir I solved the whole thing And got the correct answer 32 Thanks for the hints and helping me out I was the only one in class who solved the difficult problem 🙏🙏🙏🙏 Love from India 🇮🇳🇮🇳

Yo hello bro , I actually wanted to ask let say You have a problem 2p^8 + 3c^9 + 3r^2 How would you find it's minimum value Can we use am gm

Clever solution! Another approach. The key : 810=729+81=9³+9² x³-x²+810=0 x³+729-x²+81=0 x³+9³-(x²-9²)=0 (x+9)(x²-9x+81)-(x+9)(x-9)=0 (x+9)(x²-10x+90)=0 => ...

Alter 2025^2--8096=2025^2-90^2+4 =(45×45)^2-(45×2)^2+4 =45^2(45^2-4)+4=45^2×43×47 +4 =43×45×45×47 +4 =(43×47+2)^2 Answer is (43×47+2)=45^2-2^2+2=45^2-2=2025-2=2023

2025^2-8096=(45×45)^2-8100+4 =(45×45)^2-(2×45)^2+4 =(45^2)^2-2×45^2×2+2^2 =(45^2-2)^2 Answer is 45^2-2=2025-2=2023.

Good problem on rectangular hyperbola

so much different names just for titu's lemma! (bergstrom's inequality, engel's form, etc) I wonder if there are more

Iterative process resulting in a fixed point?

Amazing solutions! Thanks for sharing!

I like Lagrang Multiplay

We probably can’t think of this solution in 9mins😮 I understand why they give us 1.5hours to solve a problem

Beautiful solution! Thanks for sharing!

stop with that stupid intro music

What the about Lagrang multiplayer ?

J = 1000 - 3(x^4+2y^2+2y^2+4z^4) now product of x^4 , 2y^2 , 2y^2 , 4y^4 is 160000 ( constant) (because xyz = 10) hence their sum is minimum when they are equal in this case each of them is equal to = (160000)^(1/4) = 20 thier sum is 4× 20 = 80 J (max) = 1000 - 3×80 = 760 also x^4 = 2y^2 = 4z^4 = 20 gives x = 20^(1/4) y = √10 z = 5^(1/4) ❤ Happy new year (1+2+3+4+5+6+7+8+9)^2 sir 😊

Nice solution! Thanks for sharing! And Happy New Year to you!🎉

Exp=2025^2-4*2025+4 =(2025-2)^2=2023^2 . So Sqrt =2023

I like the problem. Although I solved the problem using a different method, I think promoting the Cauchy-Schwarz Inequality is a good idea.

Thanks sir🙏🏿🔥 very good explanation

Nice solution! Thanks for sharing!