
- 11
- 127 294
Ben Tupper
เข้าร่วมเมื่อ 30 มี.ค. 2014
Rudin Illustrated Proof: Closed subsets of compact sets are compact.
I illustrate and explain Walter Rudin’s proof for the following theorem from Principles of Mathematical Analysis:
Theorem 2.35 Closed subsets of compact sets are compact.
The argument is Rudin’s but the wording, illustrations, and music are my own.
Theorem 2.35 Closed subsets of compact sets are compact.
The argument is Rudin’s but the wording, illustrations, and music are my own.
มุมมอง: 1 586
วีดีโอ
Rudin Illustrated Proof: Compact subsets of metric spaces are closed.
มุมมอง 4K3 ปีที่แล้ว
I illustrate and explain Walter Rudin’s proof for the following theorem from Principles of Mathematical Analysis: Theorem 2.34 Compact subsets of metric spaces are closed. The argument is Rudin’s but the wording and illustrations are my own.
Introduction to Group Theory
มุมมอง 2.7K3 ปีที่แล้ว
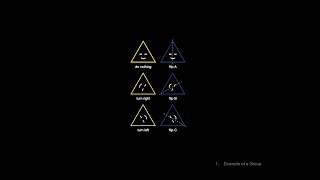
What is Group Theory? A friendly introduction to the study of groups. This video covers: 0:00 Introduction 0:50 Example of a Group 7:27 Definition of a Group 13:10 Variety of Groups The music is my own. Resources: 3Blue1Brown video: th-cam.com/video/mH0oCDa74tE/w-d-xo.html Visual Group Theory by Nathan Carter: textbookbasics.com/product/visual-group-theory-maa-problem-book-series-1st-edition-by...
The Square Root of 2 is Irrational: Proof by Contradiction
มุมมอง 4494 ปีที่แล้ว
The Greek mathematician Hippasus was (allegedly) drowned for daring to prove that the square root of 2 is an irrational number. Here is the proof.
Splitting the "L"
มุมมอง 1965 ปีที่แล้ว
Puzzle: Can you devise a method to bisect any L shape using a single line?
The Cat and Mouse Puzzle
มุมมอง 3966 ปีที่แล้ว
You are a cat, trying to catch a mouse. What is your best strategy?
The Circular Train Puzzle
มุมมอง 8K6 ปีที่แล้ว
You are trapped in a circular train. What is the best method for figuring out how many train cars there are?
What is a Rep-tile?
มุมมอง 2.4K6 ปีที่แล้ว
Rep-tiles are geometric shapes that can be decomposed into smaller, similar shapes.Finding and identifying them is like a biological endeavor. Related topics: Geometry, tessellations, fractals.
What is a Tessellation?
มุมมอง 98K6 ปีที่แล้ว
A tessellations can be beautiful and complex while its underlying structure is simple. Here are two methods for making tessellations like the great M.C. Escher's.
What are Twin Primes?
มุมมอง 9K6 ปีที่แล้ว
Twin Primes are pairs of primes whose difference is 2. The Twin Prime Conjecture posits that there are infinitely many of them, but nobody has proven it yet. Here, I dodge that question and instead show a Cute Little Fun Fact about Twin Primes.
Are There an Infinite Number of Primes? - Euclid's Proof (300 BC)
มุมมอง 6156 ปีที่แล้ว
More than two thousand years ago Euclid proved that there are an infinite number of prime numbers. If you're feeling a little behind, here was his reasoning.








Thank you, that was so useful, I would like to know how it was animated, I'm planning a class in which that kind of presentation would be perfect
well done!
😊
Wow this is exactly what i was looking for ! Thanks ! ❤ I had to page through so many yt searches before finally finding this video. It was a pain. Too many people surfing on the einstein tiling and too many people making 20min videos that just say the most basic info about tesselation (and they actually often say wrong stuff also because they're not rigorous).
helllllllloo
hi ingi
thank you for the help
heh
Thank you for the help
Im here cause of math class
No
Yes
I am here cause of math not u
That was very helpful, Thanks!
Cute video
How to do the hexagon?
Great explanation, thank you!!
U are bestttttt, so helpfullll. This must have taken sooo much efforts
Please make more!!!!
I wanna be able to show that for a given x in W_q and y in V_q then d(x,y)>0 this would show disjointness of W_q and V_q right?
correct, u can use triangle inequality
A simple improvement is moving forward after going 2n places until you reach a car in the same state as the first car before doubling back. Therefore growing n a little quicker.
I wonder if by setting the cars you've gone through to a specific pattern you might be able to grow n quicker. I suspect turning on powers of 2 only may have utility. Or only turning on one.
I think doing something like this should allow you to double n moving forward instead of backtracking whenever the end of the line doesn't match the start of the pattern. So for example if you turn all lights on, only need to turn back when the last car is on. (in this case moving you may want be required to turn everything on moving clockwise everything off moving counterclockwise)
Good explanation..
Super easy. Since there is no mention the cars are moving, we can assume they are fixed in space. Using a compass, note your starting point relative to the compass. Proceed through the cars counting until you have reached your original point on the compass. Done.
Since one of the assumptions is a circular train, can you take advantage of the fact that the minumum train length is 3? A one car train cannot have its right exit adjacent to its left entrance. Also, a two car train would not be able to connect its exits and entrances. A three car train would be more like an equilateral triangle, but it would approximate a circular train.
Thank you so much! Both of your Rudin videos were very helpful :) you should continue with these!
Efficient? Turning all these lights on is going to really increase energy consumption! :D
Such a good video, thanks man!
What kind of tesselation is this? A reflection, translation or rotation? Thank you.
Awesome Video! 👍🏻👍🏻👍🏻👍🏻
I absolutely loved this video. Inspirational. Thank you.
It is simpler to say that the list of primes is endless because the lowest factor greater than 1 of p!+1 must be a prime number and must be greater than p. This is not actually a 'proof by contradiction'.
Kei bujena♥️
This is amazing
Not sure if this is more efficient, but i think there's a number of ways to go about solving this puzzle by using alternating on/offs to count. For example, the most primitive one would be to just walk the length of the train and turn everything on, then alternately switch off the lights and count the number of switches you've pressed, and once you reach a car-oh just realized if the train has an even number of cars you're sorta stuck and also how do you even know when to stop doing the switch everything on in the first place? LMAO there goes the whole thing welp, fun puzzle tho
merveilleuse
Bravo! This is the first video I saw on TH-cam that actually demonstrates how Escher played with geometry, rather than some random translation/rotation/reflection.
"They'll snuggle together...like Teddy Squares"... Anyway, thanks for the demo (four years ago).
This is the best explanation of this proof I have ever seen. Thank you so much!
nice video
Very good!
WOW great !
Hello. great video. What program are you using to make the shapes e.g. pegasus from the square? I'd like my students to make a tessalation but on the computer. not with paper
Broooo I finally found the perfect video after an hour of searching
Thanks for the explanation keep up the good work
🙏Thank you, this was very helpful to understand the principle.
You can do slightly better than saying prime pairs sandwich a multiple of six. The table in the video is a simple expression of the idea of wheel factorization (there's a Wikipedia page, just like for sexy primes!). The next larger table would have thirty columns, and an examination of those columns would eliminate one of every five multiples of six as a candidate, because one of the columns would have no possible primes past some lower bound. After that, you could build a table with 210 columns and eliminate another class of multiples of six as sandwiched values, etc. An observation about this idea, though, is that it really doesn't really narrow down prime pairs so much as it just narrows down primes. As should be obvious from the six table, it's not actually prime pairs that are excluded--it's primes that are excluded and the exclusion of prime pairs just sort of comes along for the ride.
This is very interesting! I hope you don't mind my adding your video to my custom M.C. Escher playlist! th-cam.com/play/PLjoG5aXflB9woFTm0Q_yFCZICCejQb_3u.html
bro , it is the best algebra tutorial ever
what if i just count the light switches? would that count?
God level 😀😀😀😀😀
Amazing explanation...need more buddy💯💯
So these are regular tessellation right??
Wow, what a beautiful and simple way to prove this! Thank you! Both your channel and this video are underrated