
- 36
- 204 129
Caspar Hewett
United Kingdom
เข้าร่วมเมื่อ 11 ก.ย. 2012
Short videos covering various aspects of fluid mechanics, civil engineering hydraulics and computational hydraulics, including hydrostatics, derivations of the fundamental equations (conservation of mass, energy and momentum), flow measurement (weirs and orifices), finite difference methods for advection and diffusion.
Eigenvalues and Eigenvectors
Introduction to eigenvalues and eigenvectors motivated by considering how matrices can be thought of as mappings or transformations.
มุมมอง: 95
วีดีโอ
Fourier series for periodic functions
มุมมอง 782 หลายเดือนก่อน
How to generate a Fourier series, a means of expressing a periodic function as the infinite sum of trigonometric functions. A Fourier series is derived for a square wave, a function that exhibits discontinuities, and the properties of partial sums of the infinite series are examined, leading to a discussion of Gibbs phenomenon.
The rules of logarithms
มุมมอง 452 หลายเดือนก่อน
Presentation of the rules of logarithms derived from the rules of indices.
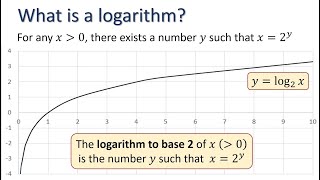
Logarithms 1: What is a logarithm?
มุมมอง 647 หลายเดือนก่อน
Definition of what is meant by a logarithm motivated by examining the behaviour of the exponential function to base 2.
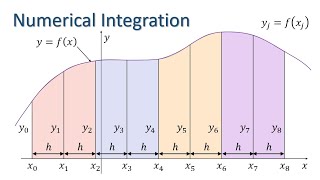
Numerical Integration - trapezium rule and Simpson's rule
มุมมอง 1037 หลายเดือนก่อน
Derivation of two methods for performing numerical integration - the first, the trapezium or trapezoidal rule, is a first order method and the second, Simpson’s rule, is second order.
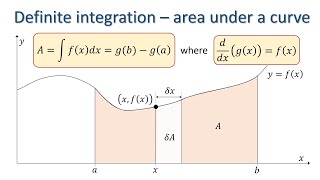
Definite Integration
มุมมอง 578 หลายเดือนก่อน
This video motivates the process of definite integration as a means of finding the area under a curve and examines how to use definite integration to calculate the average value of a function. For those unfamiliar with indefinite integration, which is the reverse of differentiation, then you should watch my video “What is Integration?” before this one.
Non-linear equations: The Newton-Raphson method
มุมมอง 49610 หลายเดือนก่อน
Derivation and example applications of the Newton-Raphson method, which is an iterative numerical procedure for finding the root of a non-linear equation.
Stability & Accuracy of Numerical Schemes (2024)
มุมมอง 58510 หลายเดือนก่อน
Definition of terms stability and accuracy and discussion of four features of numerical schemes that effect the stability and accuracy of their solutions: Numerical diffusion (which was discussed in depth in a previous video), bounded solutions, the Courant-Friedrichs-Lewy, or CFL, condition, & linear stability analysis. This video links with previous videos on Finite Difference Schemes for Adv...
Understanding Calculus: What Is Integration?
มุมมอง 89ปีที่แล้ว
Introduction to indefinite integration, which is the reverse of differentiation. This video discusses why there is a constant of integration in this procedure and what it means, and presents examples of indefinite integration of functions including powers of x, exponential functions, the natural logarithm and the primary trigonometric functions: sine, cosine and tangent.
Understanding Exponential Functions
มุมมอง 64ปีที่แล้ว
Introduction to exponential functions (functions of the form y = a to the power of x). This video covers the functions with base 2 (2 to the power of x), and base 3 and introduces the special case, usually called the exponential function, which has base e and has special properties under differentiation. The natural logarithm is introduced as the inverse of the exponential function and its diff...
The Chain Rule (Calculus 3)
มุมมอง 85ปีที่แล้ว
Derivation of the chain rule which is the method used to differentiate a function of a function.
Differentiating Trigonometric Functions (Calculus 2)
มุมมอง 72ปีที่แล้ว
The differentials of sine and cosine are derived from first principles. This video includes the definition of the radian and first order small angle approximations for sine and cosine.
What Is Differentiation? (Calculus 1) Differentiation from first principles.
มุมมอง 191ปีที่แล้ว
Introduction to the notion of differentiation to describe the instantaneous rate of change of a function. A general expression for the differential or derivative is derived and an example of differentiation from first principles given using the function f(x) = x cubed.
Finite Difference Schemes for Advection and Diffusion
มุมมอง 16K3 ปีที่แล้ว
Finite Difference Schemes for Advection and Diffusion
Implicit Upwind Finite Difference Solution to the Advection Equation
มุมมอง 4.4K3 ปีที่แล้ว
Implicit Upwind Finite Difference Solution to the Advection Equation
Explicit Upwind Finite Difference Solution to the Advection Equation
มุมมอง 13K3 ปีที่แล้ว
Explicit Upwind Finite Difference Solution to the Advection Equation
Fluid Mechanics: The Continuity Equation
มุมมอง 2.1K4 ปีที่แล้ว
Fluid Mechanics: The Continuity Equation
Finite difference approximations to the first derivative
มุมมอง 6K4 ปีที่แล้ว
Finite difference approximations to the first derivative
Hydraulic River Modelling: Muskingum-Cunge
มุมมอง 4.3K4 ปีที่แล้ว
Hydraulic River Modelling: Muskingum-Cunge
Kinematic Wave Solution to 1D Shallow Water Equations
มุมมอง 6K4 ปีที่แล้ว
Kinematic Wave Solution to 1D Shallow Water Equations
Hydrostatics: Hydraulic Thrust Calculation Using Pressure Prisms
มุมมอง 2.5K4 ปีที่แล้ว
Hydrostatics: Hydraulic Thrust Calculation Using Pressure Prisms
Hydrostatics: Hydraulic Thrust On Plane Surfaces
มุมมอง 2.1K4 ปีที่แล้ว
Hydrostatics: Hydraulic Thrust On Plane Surfaces
Hydrostatics: Hydraulic Thrust on Curved Surfaces Part 2: Examples
มุมมอง 5834 ปีที่แล้ว
Hydrostatics: Hydraulic Thrust on Curved Surfaces Part 2: Examples
Hydrostatics: Hydraulic Thrust on Curved Surfaces Part 1
มุมมอง 9374 ปีที่แล้ว
Hydrostatics: Hydraulic Thrust on Curved Surfaces Part 1
Fluid Mechanics: Applications of the Fundamental Equations
มุมมอง 7194 ปีที่แล้ว
Fluid Mechanics: Applications of the Fundamental Equations






Hi, you defined diffusive wave approx. as a Steady non - uniform flow . you mentioned that this approximation would produce a this inflow hydrograph. This hydrograph depends on time but diffusive wave equation is steady. How it can be possible
Let the the fluid has uniform flow throughout the pipe. Is that mean there is no momentum change in the pipe?
Yes, that is correct. Momentum is conserved.
Anyone know where the coefficient of discharge comes from… seems to be one of engineerings finest mysteries
It is an empirical parameter which is intorduced to take account of energy losses - for the idealised case the coefficient is one. Thus, for a real weir we haev to calibrate to find cd.
🎉🎉🎉
Thank you Sir
Thank you so much
Good to see you're still at work! Best regards Terry J
great job
i wish you would be my teacher. amazing
EXCELLENT-- WHICH UNIVERSITY ? -WHICH COUNTRY ?
Newcastle University, UK
@@CasparHewettFluids thank u sir
Please someone help me out, I have a tube well with 3 inches delivery and water is pulled by a 7.5 hp submersible pump system. What I am planning to do is to reuse the water force which falls out and to produce electricity or mechanical power. What output can be obtained and which system is more efficient, micro hydro turbine or a propeller.
Wouldn’t be worth the power you created
@@robertmulderrig7384 shut up and help
Hi, Thank you for the good explanation. I'm personally interested in how you can use it to solve a nonlinear reaction diffusion equation. How would you go about analysis its stability in relation to the Von Neumann Stability condition? Thank you in advance.
👌👌👌
Was this video inspired by a publication or academic resource? I would be interested in learning more about the stability analysis!
No, I wrote the material myself for a course. I will be publishing a book on Computational Hydraulics later this year, though, which will expand on this material.
Why is the momentum force in the opposite direction as the pressure force? Seems like they would both be acting in the same direction, no?🤔
There are two elements of the momentum. The momentum into the control volume, which acts in the same direction as the pressure and the momentum out of the control volume which is in the opposite direction to the pressure
The pressure forces are those acting on the control volume, which is why they are both inward
Very good, detailed analysis. The figures and equations are beautifully rendered. Thanks!
Perfect, just explained in 5 mins what took hours to be taught badly in university.
Great video! But why can't I find anyone explaining 3-pt 1st-order FD?
Hello! Is there a way we could send you an email?
Do you have a question? I will do my best to answer it here!
Hello, what is ubar in the bousinesque equation
Is it like the average velocity or what?
@@danielhakimzambri892 yes, it is the average velocity 😉
@@CasparHewettFluids thanks
Well explained Keep up the good work 👍
Shukran jidan!
what is bournolis ?
Bernoulli was a person, but in this context I am talking about the steady state energy equation - see this video for details: th-cam.com/video/mpsm7GRyaHs/w-d-xo.html
Is the beam warming scheme is implicit
What basics should i study more to understand this?
if we consider a 90-degree bend pipe, with initial conditions as follows: inlet velocity 15 m/s, no change in cross-section area (let's say radius of 0.2 m), and we only know outlet pressure is equal to atmospheric pressure. Is Bernoulli's equation satisfied? does it mean outlet and inlet pressure are the same? in that case, there's no flow?!
Bernoulli equation is satisfied within the pipe so pressure will be constant if the pipe is horizontal, resulting in a jet at the outlet. The pressure in the pipe can't be atmospheric pressure if the water has a velocity! Conditions are different once water reaches the outlet. Thus, the problem you pose can't be solved. There is insufficient information. You would need to know the pressure in the pipe.
at 11:29 your wrote incorrect solution please review it. It should be (r - rho)*c(i+1),(j)
What a wonderful video!!!!!!
Would the vertical pressure force still be oriented downward if the curved pipe was facing down not up?
No, the pressure force always acts inwards towards the control volume so it would be acting upwards if the pipe were facing downward.
excellent explanations! I wish I had such an articulate professor when I studied open channel hydraulics at university.
Thanks 🙂
this is amazing, thank you!
Thank you professor
Great video. Thank you
The last image looks just like B-Spline basis functions. Is my assumption right, or wrong?
Thanks a lot sir.
Very well explained. Thanks a lot!
Why is density not included in the Bernoulli equation?
P/dg=H-z1
See th-cam.com/video/mpsm7GRyaHs/w-d-xo.html for a full explanation - density does appear in the equation!
Well presented, thank you Caspar!
It helped me a lot. Can you tell me how did you define initial distribution?
How do we determine the direction of pressure force?
We are considering the forces on the control volume, so the pressure force is acting inwards on that control volume (there is an equal and opposite pressure force outward, but that isn't relevant to the calculation) thus it is acting to the right on the left hand side and to the left on the right hand side.
such a nice video! well done!
hello, i stumbled upon a exercise that was similar to the last example but the curve was divided in half by two fluids. Would the resultant vertical force be the same?
The best 1d hydrodinamic equation explanation video!!!
u da mvp!
Thank you. I learned a lot from this video
Very good explanation. Thank you (again), Caspar.
Thank you. Well explained.
Very neatly explained, Caspar; thank you.
Great video
This is priceless!! cant be explained in a better way. Thank you for your effort.