
- 49
- 18 631
QAMO 3020
เข้าร่วมเมื่อ 19 มี.ค. 2020
วีดีโอ
Some guidance on trembling hand perfect Nash Equilibrium
มุมมอง 2.1K4 ปีที่แล้ว
Some guidance on trembling hand perfect Nash Equilibrium
Extensive form games with imperfect information - 10
มุมมอง 2744 ปีที่แล้ว
Extensive form games with imperfect information - 10
Extensive form games with imperfect information - 9
มุมมอง 2674 ปีที่แล้ว
Extensive form games with imperfect information - 9
Extensive form games with imperfect information - 5
มุมมอง 4064 ปีที่แล้ว
Extensive form games with imperfect information - 5
Extensive form games with imperfect information - 8
มุมมอง 3224 ปีที่แล้ว
Extensive form games with imperfect information - 8
Extensive form games with imperfect information - 6
มุมมอง 2234 ปีที่แล้ว
Extensive form games with imperfect information - 6
Extensive form games with imperfect information - 7
มุมมอง 1874 ปีที่แล้ว
Extensive form games with imperfect information - 7
Extensive form games with imperfect information - 4
มุมมอง 2444 ปีที่แล้ว
Extensive form games with imperfect information - 4
Extensive form games with imperfect information - 3 - A simple card game
มุมมอง 4314 ปีที่แล้ว
Extensive form games with imperfect information - 3 - A simple card game
Extensive form games with imperfect information - 2
มุมมอง 6544 ปีที่แล้ว
Extensive form games with imperfect information - 2
Extensive form games with imperfect information - 1
มุมมอง 1.7K4 ปีที่แล้ว
Extensive form games with imperfect information - 1
Bayesian games - First price common value auctions - numerical example
มุมมอง 4544 ปีที่แล้ว
Bayesian games - First price common value auctions - numerical example
Bayesian games - second price common value auctions - numerical example
มุมมอง 2684 ปีที่แล้ว
Bayesian games - second price common value auctions - numerical example
Bayesian games - 22 - First price common value auctions
มุมมอง 3684 ปีที่แล้ว
Bayesian games - 22 - First price common value auctions
Bayesian games - 19 public good provision
มุมมอง 5174 ปีที่แล้ว
Bayesian games - 19 public good provision
Bayesian games - 21 second price common value auctions
มุมมอง 3444 ปีที่แล้ว
Bayesian games - 21 second price common value auctions
Bayesian games - 20 common value auctions (introduction)
มุมมอง 2364 ปีที่แล้ว
Bayesian games - 20 common value auctions (introduction)


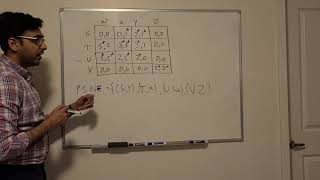






Finally a professor whose lecture i can understand. This subject is so difficult you explained this topic very well.
What is that alpha and gama?
Helpful explanation :)
What an explanatory exemplification of the matter! Thanks, sir
Thanks for explanation. You look great btw!)
Really helpful!
thxx! you really explained it well! I seldom understand stuff from YT but i understood this rly well. My assignment was on trembling hand perfection without it being actually taught in class, so this is rly helpful!
I think it would be a better example if (B,C) and (M,R) were (0,3) and (3,0) respectively. Then the probabilities would be more important.
Hey, how can I get in touch with you for further questions?
gracias pa
I really don't get it.
Let me do a little explanation. For Player1, Player 1 Plays T, and Player 2 palys L. but Player1 knows Player 2 may play C or R some of the time. Hence if Player 2 plays C or R, Player 1 has a profitable deviation Playing M or B. Next, we find out what are Player1's payoffs playing M or B. The largest Payoff for Player 1 knowing that Player 2 plays L with probability q1, Player2 Plays C with probability q2 and Player2 Plays R with probability 1 - q1- q2 ( Note that the sum of the probabilities must equal 1 i.e q1+q2+1-q1-q2=1) will be his THP NE. Solving the payoffs for Player 1 playing M and for playing B we have U(M) = 0(q1) + 1(q2) +2(1-q1-q2) = 2 - 2q1 - q2 U(B) = 0(q1) + 0(q2) +2(1 - q1 - q2) = 2 - 2q1 - 2q2 Since q1 is a positive number between 0 and 1, and q2 is a positive number between 0 and 1. It implies the payoff for player 1 playing M is greater than her payoff playing B. Hence M is the THP NE for Player 1. i.e U(M)>U(B) (because subtracting q2 from 2 -2q1 is greater than subtracting 2q2 from 2 -2q1) Similar argument can be made for Player 2 by calculating the payoff for player 2