วีดีโอ

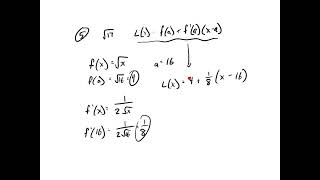
:D

thanks sir

You saved me, thanks a lot

Is this from Friedberg insel and spence?

I’m slightly confused on why the last example has a unique solution, while example 2 had a nontrivial solution

Is ky solve questions chahiye plzzzz 4.1 ky

Great vid

thank you markiplier

Thank you, this has helped me fill in the blanks that my statistic teacher was not able to explain during class. :)

that’s so funny, I watch this channel and 3brown1blue

you have a nice voice, easy to listen to

Where’s 2.4?

very good video. helped alot. thank you for sharing

I could be wrong but at 13:44, I think he forgot to put in a -1. I don't see any reason why he didn't carry over the row 1,2,-1 during the row operation, so I'm pretty sure he mistakenly wrote 1 2 1 in the determinant. Could be wrong but lmk if anyone else agrees. Love the videos btw!!!

thank you

these videos are so clutch

Thanks for the helpful video, you explained very well in 24 minutes what my professor couldn't in 1.5 hours. Again, thank you.

"when i said 4, i meant 3" had me dead ngl 😂😂

U r my prof

I'm taking applied linear algebra in the summer and we have 5 weeks to learn everything. I was going to drop but it was a day later before I could. Test every week and 2 quizzes every week. This is such a horrible way to learn math...

i love u <3333

Let M and x0 be as in Example 3. a. Compute the population vectors xk for k = 1,2,...20. Discuss what you find. b. Repeat part (a) with an initial population of 350,000 in the city and 650,000 in the suburbs. What do you find? Help me pls

this is hard to understand for non math majors. im an engineering major and i had a really hard time understanding this.

i appreciate your work thank you so much :)

This makes my brain hurt but it makes me feel smart

Yeah everything really is just linear algebra, all of algebra calc ect is just…linear algebra.

This video helped a lot, always been kinda bad with diagonalzation this semester

This kinda reminds me of my circuits class

This section seems challenging because of all the work involved and a lot of going back and forth between the steps to find the solution.

i was told that pivot doesn’t necessary have to be 1 it can be any non zero number so why didn’t u consider column 3 for basis for col A?

In my opinion, Linear Algebra is just a deeper explanation of what we already know.

Video 3 completed for rewatching all the videos for this unit

Video 2 completed for rewatching them all

One video down for rewatching them all

Its interesting that you can take pretty much use any polynomial equation to essentially find the scalars for that polynomial using this set up. I might try this in other settings as well in the future if I get the chance.

Hey in example 3 you wrote sigma originally with 6sqr(10) and 3sqr(10) but then in the final answer you wrote them both as being divided by the square root of 10 instead. was that on purpose?

Looking at the way we computed X^TAx made me realize that it is very similar to the way some of us are taught to form equations instead of techniques like foil. It makes me think that if I only knew linear algebra as a baby I would've conquered the world.

I've recently come to the conclusion that rather than learning anything new, we are actually learning what we already know from a deeper perspective and developing a greater understanding of its applications.

Thank you so much for these videos ! *2

Visual representation is always helpful

I appreciate using past knowledge and techniques to new topics. Specially since I took Calc 3, using projections and orthogonality are both a lot more interesting. Are there past chapters where we could simplify things if we knew about symmetric matrices?

Appreciated the visual representation of what the definition means and breaking down the problems to illustrate the concepts. It made the material much easier to understand.

in the least-squares error problem you said any other point would be further than 9.2, but our definition says the least-squares solution is less than or equal to any other point. How does that work?

Pictorial representation really helps me understand the topic better. It helps in visualizing the problems and solutions.

I found the procedure to be super straightforward, I really like this. I think it is pretty interesting to create orthogonal sets, what type of applications will we have for this? Does an orthogonal set basically give us a new set of axis we can follow?

The best approximation theorem simplifies complex problems by providing a clear path to finding optimal solutions