
- 1 478
- 2 880 117
Zak's Lab
United States
เข้าร่วมเมื่อ 17 ส.ค. 2020
Physics and Math with an emphasis on WHY!
My name is Zak Hannan, and I'm a college professor of physics and mathematics with 20 years of full-time teaching experience.
Zak's Lab is a physics and calculus instruction channel with hundreds of short lecture and example videos produced to "flip" my courses, and it is also an excellent resource for physics and math self-study.
Currently, my channel covers the following college and AP high school courses:
College Physics I and II (trigonometry based)/AP high school physics.
Engineering Physics I and II (calculus based).
Calculus I/AP high school calculus.
Calculus II
Browse dozens of playlists organized into the corresponding college course category. To see the full collection of playlists, please click the "playlists" button, as they do not all appear on the cover page.
Thanks for watching! -- Zak
My name is Zak Hannan, and I'm a college professor of physics and mathematics with 20 years of full-time teaching experience.
Zak's Lab is a physics and calculus instruction channel with hundreds of short lecture and example videos produced to "flip" my courses, and it is also an excellent resource for physics and math self-study.
Currently, my channel covers the following college and AP high school courses:
College Physics I and II (trigonometry based)/AP high school physics.
Engineering Physics I and II (calculus based).
Calculus I/AP high school calculus.
Calculus II
Browse dozens of playlists organized into the corresponding college course category. To see the full collection of playlists, please click the "playlists" button, as they do not all appear on the cover page.
Thanks for watching! -- Zak
Archimedes principle: iron floating in mercury, find the submerged percent.
Mercury is more dense than iron, and that means an iron block floats in mercury!
In this problem, we compute the submerged percent of an iron sample floating in mercury. We start with a force diagram of the floating iron block, with the weight, mg, pointing down, and the buoyant force F_B pointing up. The buoyant force is equal to the weight of the displaced fluid, in other words, the weight of the submerged volume of the iron block.
We give a quick reminder of the definition of density as mass divided by volume, and that can be turned around to say that mass is density times volume - a relation that will be useful a couple times in our calculation.
Since the iron block is in equilibrium, F_B=mg, and now we can replace the buoyant force with the details using Archimedes' principle: the buoyant force is equal to the density of mercury times the submerged volume of the block times g. On the right hand side, the weight of the iron block is given by the density of iron times the volume of the iron block times g.
Solving for the submerged volume divided by the total volume of the iron block, we obtain the percent submerged for a block of iron floating in merury.
In this problem, we compute the submerged percent of an iron sample floating in mercury. We start with a force diagram of the floating iron block, with the weight, mg, pointing down, and the buoyant force F_B pointing up. The buoyant force is equal to the weight of the displaced fluid, in other words, the weight of the submerged volume of the iron block.
We give a quick reminder of the definition of density as mass divided by volume, and that can be turned around to say that mass is density times volume - a relation that will be useful a couple times in our calculation.
Since the iron block is in equilibrium, F_B=mg, and now we can replace the buoyant force with the details using Archimedes' principle: the buoyant force is equal to the density of mercury times the submerged volume of the block times g. On the right hand side, the weight of the iron block is given by the density of iron times the volume of the iron block times g.
Solving for the submerged volume divided by the total volume of the iron block, we obtain the percent submerged for a block of iron floating in merury.
มุมมอง: 65
วีดีโอ
Given the phase space plot and total energy for an oscillator, find the mass and spring constant.
มุมมอง 20212 ชั่วโมงที่ผ่านมา
Given the phase space plot for a simple harmonic oscillator, we identify the points at which all the energy is kinetic or potential energy. At the top and bottom of the phase space trajectory, we have the points of maximum speed and zero displacement, so all the energy is kinetic. We take the given total energy of the SHO and set it equal to 1/2mv_max^2, then solve for the mass of the oscillato...
How to show conditional convergence of an alternating series (-1)^n*n/sqrt(n^3+1).
มุมมอง 2314 ชั่วโมงที่ผ่านมา
We test the convergence of an alternating series (-1)^n*n/sqrt(n^3 1), starting with the test for absolute convergence (because if we can show absolute convergence, it automatically implies ordinary convergence of the series). The series of absolute values approaches the terms of the divergent p-series 1/sqrt(n) in the large n limit, so we perform a limit comparison test and find that our serie...
Test convergence with the limit comparison test: sum of 3/(n^2-2).
มุมมอง 18414 ชั่วโมงที่ผ่านมา
For the infinite series: sum 3/(n^2-2) we test convergence with the limit comparison test. We notice at a glance that this series "essentially" behaves like 1/n^2 in the large n limit, and sum (1/n^2) is a convergent p-series (a result we proved previously by using the integral test). Unfortunately, a direct comparison is not possible because the terms of 1/(n^2-2) are larger than those of 1/n^...
Test the convergence of the series e^n/n^3 - nth term test with L'Hopital's rule.
มุมมอง 4316 ชั่วโมงที่ผ่านมา
Given the series e^n/n^3, we immediately see that it's going to diverge because we remember that exponentials outpace the growth rate of polynomials. To prove the divergence of the series, we use the nth term test with L'Hopital's rule. We take the limit as n goes to infinity of e^n/n^3 and apply L'Hopital's rule multiple times to arrive at a result of infinity as we suspected. This is an extra...
How to compute the limit of a sequence with factorials. a_n=(2n-1)!/(2n+2)!
มุมมอง 2816 ชั่วโมงที่ผ่านมา
We compute the limit of the sequence a_n=(2n-1)!/(2n 2)! by splitting off factors from the larger factorial until we can cancel the numerator. After that, we can handle the limit at infinity informally by seeing that the denominator grows to infinity as the numerator stays constant, so the limit is zero. Alternatively, we can pretend to be mathematically rigorous by expanding the denominator in...
Limit of the sequence a_n=(n+1)/(9n-1) | Physics Class vs. Calculus Class
มุมมอง 43716 ชั่วโมงที่ผ่านมา
We compute the limit of a simple sequence (n 1)/(9n-1) from two different perspectives: the physics class perspective relying on quick, intuitive and reliable approximations vs. the introductory calculus class perspective in which we agonize over the limit laws and the manipulation of the limit in order to use the limit of 1/n as n goes to infinity. As a professor who wears both hats (math and ...
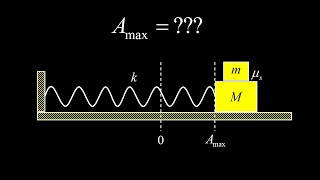
Find the maximum amplitude so the block doesn't slip!
มุมมอง 12519 ชั่วโมงที่ผ่านมา
Given a harmonic oscillator on a smooth surface with spring constant k and mass M, we stack a second block m on top of M feeling a coefficient of static friction mu_s and calculate the maximum amplitude so the second block doesn't slip (little m). We begin by viewing the two masses as a single mass m M and when x is equal to the amplitude, we have our maximum spring force, therefore the maximum...
Buoyancy problem: find the mass of lead needed to sink a wood block (Archimedes' Principle)
มุมมอง 11519 ชั่วโมงที่ผ่านมา
We apply Archimedes' Principle to calculate the mass of lead needed to sink a wood block, specifically the mass required for the wood and lead to stay submerged in perfect equilibrium. To start things out, we make complete force diagrams for the wood block and the unknown lead mass. The block has buoyant force pointing up and weight and tension pulling down. The lead mass has buoyant force and ...
How to make a phase space plot for the simple harmonic oscillator.
มุมมอง 483หลายเดือนก่อน
Given the mass, spring constant and amplitude of a simple harmonic oscillator, we construct a phase space plot for the simple harmonic oscillator. The phase space plot for a harmonic oscillator is a graph of velocity vs. position, and the oscillator traces out a trajectory in phase space (ordered pairs consisting of position and velocity) as it evolves in time. Taking a look at the expression f...
Find the speed of a harmonic oscillator at a given position.
มุมมอง 140หลายเดือนก่อน
Given the mass, spring constant and amplitude of a simple harmonic oscillator, we find the speed of the oscillator at a specific position of x=10cm. This is an energy conservation problem, where the given spring constant and amplitude allow us to find the total initial energy as 1/2kA^2. The final total energy of the oscillator has both kinetic and potential energy components, 1/2kx^2 and 1/2mv...
Find the amplitude and maximum acceleration of a simple harmonic oscillator.
มุมมอง 85หลายเดือนก่อน
Given the speed of a simple harmonic oscillator as it passes through equilibrium, we find the amplitude and maximum acceleration of the harmonic oscillator. Finding the amplitude of the oscillator is an energy conservation problem: in the initial state, all the energy is kinetic because the spring is at its relaxed length in the initial state of the system. In the final state, all the energy is...
Find the maximum speed of a pendulum, the period and the time to get to maximum speed.
มุมมอง 220หลายเดือนก่อน
Given the length of a simple pendulum released from rest at a given small angle, we compute the time it takes for the pendulum bob to reach its maximum speed, then we find the maximum speed of the pendulum bob. The maximum speed of the pendulum occurs at the lowest point on its path which takes a time of one quarter period, so we use the period formula for a pendulum: T=2pi*sqrt(L/g) and divide...
Find the spring constant given the position time graph for a simple harmonic oscillator.
มุมมอง 106หลายเดือนก่อน
Given the position time graph for a simple harmonic oscillator and given the mass of the oscillator, we calculate the spring constant by using the period formula for a spring and mass system T=2pi*sqrt(m/k). Along the way, we use the position time graph for the simple harmonic oscillator to determine the period and frequency of oscillations and the amplitude of oscillations, then we use the kno...
Converting frequency to period for a sound wave (middle C or C4).
มุมมอง 84หลายเดือนก่อน
Converting frequency to period for a sound wave (middle C or C4).
Period of a physical pendulum: uniform disk drilled off-center.
มุมมอง 384หลายเดือนก่อน
Period of a physical pendulum: uniform disk drilled off-center.
Period of oscillation for a thin ring physical pendulum.
มุมมอง 229หลายเดือนก่อน
Period of oscillation for a thin ring physical pendulum.
Atwood machine with a heavy pulley: find acceleration and angular displacement.
มุมมอง 669หลายเดือนก่อน
Atwood machine with a heavy pulley: find acceleration and angular displacement.
Solve elastic collisions using the center of mass frame trick!
มุมมอง 521หลายเดือนก่อน
Solve elastic collisions using the center of mass frame trick!
Find the Laplace transform of the sine function (Laplace transform of sin(t)).
มุมมอง 647หลายเดือนก่อน
Find the Laplace transform of the sine function (Laplace transform of sin(t)).
Gravitational self-energy of a uniform sphere.
มุมมอง 250หลายเดือนก่อน
Gravitational self-energy of a uniform sphere.
Period of oscillation for a rectangular slab physical pendulum.
มุมมอง 2962 หลายเดือนก่อน
Period of oscillation for a rectangular slab physical pendulum.
Moment of inertia of a rectangular slab with rotation axis perpendicular to the slab.
มุมมอง 2082 หลายเดือนก่อน
Moment of inertia of a rectangular slab with rotation axis perpendicular to the slab.
Integral of sin^n(x) reduction formula derived using the integration by parts "looping trick".
มุมมอง 6732 หลายเดือนก่อน
Integral of sin^n(x) reduction formula derived using the integration by parts "looping trick".
u-substitution combined with integration by parts: integrate cos(sqrt(x))!
มุมมอง 1782 หลายเดือนก่อน
u-substitution combined with integration by parts: integrate cos(sqrt(x))!
Find the integral of sin^3(x)/sqrt(cos(x)).
มุมมอง 3452 หลายเดือนก่อน
Find the integral of sin^3(x)/sqrt(cos(x)).
Integral of cos^2(pi*x) on [0,2] + an average value integral trick.
มุมมอง 1932 หลายเดือนก่อน
Integral of cos^2(pi*x) on [0,2] an average value integral trick.
How to study physics: what my 'A' students said.
มุมมอง 7272 หลายเดือนก่อน
How to study physics: what my 'A' students said.
Find the spring constant given the maximum compression of a spring.
มุมมอง 3922 หลายเดือนก่อน
Find the spring constant given the maximum compression of a spring.
Find the final speed using a work integral with F(x)=3sin^2(pi*x).
มุมมอง 2352 หลายเดือนก่อน
Find the final speed using a work integral with F(x)=3sin^2(pi*x).






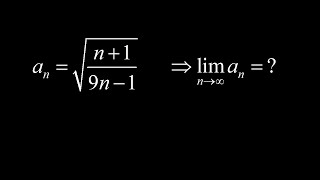

❤❤❤
It is easy to find the final velocity of the masses if you find the tension of the rope. because for 3kg : [ mg(0.5m) - Tension *( distance it travels {0.5m } ) = final kinetic energy ]
Thank you But for sure you mean that when he asks for the wavelength for example the first line in the lyman series ,so nf=1 and ni=1???
could you make a video like this, but with secθ, cscθ or tanθ ? I can’t visualize why they would diverge
What is the value of the angle?
You don't need it. By using energy arguments instead of focusing on forces, you can get the work done by friction given only the initial height and the fact that the speed is constant! z
@ZaksLab I remember last year in the physics test there was a difficult question. This video made me remember the question. It was about friction. The text of the question is ( An object is sliding an incline surface as shown in figure, if the 20% of the surface is smooth and the other is rough with μ = 0.86 . if the object starts from rest and comes to rest at the bottom. Find The angle θ = ?)
if its not 100% riggorous its 0% riggorous calc class students just put makeup on and pretend physics students is how real men calculate
why do we start the summation from n=1 even though the summations for like sinx we start from n=0 I've been really stuck on this concept
You can start from 1 or 0 as long as your summation produces all the same terms. If we started this one from 0, we could use (-1)^n for the sign alternation (starts with + then alternates), then the rest of it would be x^(n+1)/(n+1). Check to see that the first few terms are the same, and in general when you're manipulating sigma notation, you're always kind of visualizing what its expanded form is going to look like.
Can you make a more generalized video to show that 2+1/2*acceleration of gravity*t^2=1/2*acceleration of floor*t^2? The conditions that must be met for your problem like the acceleration of gravity always has to be less than the acceleration of the floor. When I saw this I wanted the answers for when the floor was moving the acceleration of gravity down and to show if the floor was moving greater than the acceleration of gravity down the ball will never make it to the floor.
Oh daـmـn school I'm still in the tenth grade I'm only 14 How can my tiny cute mind comprehend this nonsense that I won't benefit from in life or after death Nothing at all It's just torture Why should I study this Daـmـn school and study and the damned power of buoyancy I can't stop crying until💔💔
The Value of ....
Is it R waves or L waves, most destructive during a earthquake??
Does that mean in longitudinal waves the molecules do not ultimately leaves its position entirely but in transverse, the molecules actually move forward entirely?
So technically particle is doing shm basically some restoring force is acting to make its way back to his own position and tangential velocity looks like goin backwards tbh so is that the reason we have importance of shearing strain in transverse wave?
Not like this that is constructed so hard that not ok
this was awesome thank you so much!!!
you're welcome! z
Thank you! Great explanation.
you're welcome! z
Sin cos the values of sin and cos are known, the values of tan, cot and sec, csc can also be known.
Physics ninja?
You are amazing! I don't understand why profs in university can't explain all of this that simple as you
Thanks! I do have the benefit of editing, but I've also been teaching for 20 years! z
I had a similar question to this, except that the wedge moved in the opposite direction as the mass slid down (but the mass stuck onto it).... Thus, like your video theta was the wedge's angle of inclination, but due to the wedge going the other way simultaneously, the "true course" of the mass sliding down would have a steeper angle. Is it necessary that the steeper angle and theta must add up to 90? It almost feels intuitively correct, but I'm having difficulty proving it...
I haven't solved that problem in a long time, and I'm not even confident the block would slide on a straight line trajectory during the motion . . . could it be a curved path? If you're just looking for final speed at the bottom, you should be able to get it with energy conservation and conservation of momentum (x direction). I have a note on my desk right now to make a video on that problem, but it will probably have to wait until the next time I teach mechanics (fall '25). z
@@ZaksLab Thanks I'll stay tuned - my physics 1 final was just today - would you believe fall '25 is exactly the semester I'll be taking 2nd year mechanics!
Thank you
you're welcome! -z
Tamil la solra
Thank you so much, I understand everything but I don't really understand why should we derivate acceleration respect to theta, how could this give us the angle that we want? Would you please explain it.
finding minimum or maximum of a function: take the derivative and set it equal to zero. That's going to be the location of a max or min because it's the top of a hill or bottom of a valley where the slope is zero (calculus I optimization stuff), and you can usually infer which based on physical context. z
Wonderful explanation
Spanish
very helpful
cool! z
idk how you dont have more views. thank you for your videos ! subscribed
thanks for your support! -Zak
Thanks for the vid bro
you're welcome! z
Very nice video. Thanks a lot. I spent much time thinking alone about the kinetics or dynamics of rolling and rolling after rest and rolling after slipping. Nearly no one talk about it or about its intuition. I am trying to figure something in case of rolling after slipping as in your case but there is a motor which keeps applying a force. If the force applied is greater than the max static friction, then it will slip or keep slipping and there will be acceleration at the c.m. so, it keeps rotating faster due to (f.app - f.kinetic) and also the c.m keep going faster due to the (f.app - f.kinetic) so the point of contact is never 0 because the tangential velocity due to rotation is larger than the velocity of c.m. Does that mean that the wheel im this case will not roll. Chatgpt say that after some time, it will roll because angular velocity will decrease, but how will it decrease although the there is torque applied! It say kinetic friction will reduce the angular velocity, but konetic friction is constant. Can you help me?
I think you're right . . . chat gpt still makes a lot of mistakes with unusual physics problems. I write a ton of new problems for my classes every semester, and I try to push the boundaries into problems that are fairly original. If I check my solution against ChatGPT, it often makes several mistakes and needs to be "coached" through the solution, apologizing every time I point out an error. It's still a useful tool, but just try pointing out its mistakes to work toward a solution. z
Can you make a video studying the values for a to make the series 1/(ln n)^a converge?
that's an interesting idea! z
Sir got me feel sad about nodes
Thank you, I really liked how you explained what you were thinking and why you made your choices.
Glad I could help! z
You just saved me dude. Cramming for an exam and had no idea what to do but this helped a ton. Great video
glad I could help! note that if you are interested in creating math animations, you now have the secret to making polar curves spin: just plot r(theta-t), where t is the animation parameter, and you'll get a CCW rotation of the curve. z
Thank you for the wonderful video, you explained this much better than my professor did in about half an hour <3
thanks! z
Conteudo top mano (I know how to speak english btw, nice video man!)
thanks! z
Cheer~~~situated or extending across something(of a line)😅
Why do u assume the thickness to be equal to arc length instead of straight line in the middle
This is a really good question, and one that bugged me for a long time. I know there are more rigorous ways to argue this, but let's simplify the problem and compare two simpler problems from calculus: finding the volume of a sphere using thin disks vs. finding the surface area of a sphere using thin ribbons. In the volume case, you can get away with using dz for the thickness of each disk, because the tiny amount you are cutting off the curved edge is negligible compared to the volume of the disk (volume of the disk is like pi*r^2dz, but the tiny angled ring we neglect is like 2pir*1/2*dx*dz, which has a product of *two* infinitesimals in it, making it of negligible order). In the surface area using ribbons case, we don't get so lucky: the surface area of a ribbon using dz for thickness is 2pi*r*dz, and the surface area using arc increment is 2pi*r*ds or 2pi*r*sqrt(dx^2+dz^2). This time the error committed is on the same order as the quantity being calculated (one infinitesimal), and that will lead to a finite cumulative error. With experience you just kind of develop a gut instinct for how detailed you need to be in order to not create a finite error -- generally speaking, surface integrals require the extra detail of using ds, and volume integrals can be treated more coursely, using dz for thickness. Try using just a dz for thickness in the surface area of a sphere calculation, and you'll see that it underestimates the total surface area compared to using ds. Hope this helps. z
@ZaksLab yes, it helps. Thank you!!!
thank you so much
you're welcome! z
Lol big "D"
merci le frère 🔥🔥🔥
The convention for torque is that a counterclockwise motion is a positive torque. And so on.
Thanks for the explanation, nice and simple
you're welcome! z
I'm an italian guy who loves physics. I've found the best place in the world! Very good explainations
thank you! z
good
Thanks sir, helpful video
I'm wondering why can we use conservation of energy in this problem. Isn't a part of them will be taken away by friction?
This may not be a very satisfying answer, but friction is not doing net work on the system here. The reason why is that the contact point with the ramp is always stationary, so there is no mechanism for dissipating energy through slipping. Instead, the friction force is always a static friction force. But this force *is* exerting a torque on the system, and in fact it's critical to have this static friction force in order to enforce the rolling without slipping condition. The static friction force is the key to converting the rotational KE of the ball into additional height here: it supplies a torque slowing the rotation down, but simultaneously supplies a force pointing up the ramp. It is a weird thought to have friction acting as a conservative mechanism to convert one type of energy into another, but if you look at the force/torque solution of the problem, it does corroborate the answer given by energy conservation.
Thank you for your response! My another question is how would we solve the problem if the ball is allowed to both slip and roll?
@@huyviethungnguyen7788 that will depend on the angle of incline and the coefficient of kinetic friction. You'd have to do a force/torque approach to the problem instead of the energy approach.
@@ZaksLab Thanks a lot!
Is the distance traveled on this for part b only x-distance or total distance on the hypotenuse
total distance! We found a_parallel, so we're describing motion along the hypotenuse.
Thank you.
you're welcome! z
thank you so much you DON"T understand how much this helped me
Glad I could help! By the way, I recently updated this kind of problem with better production quality: th-cam.com/video/qTm3LyVVYI8/w-d-xo.html