วีดีโอ

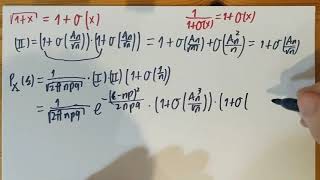
thanks for the explanation

Great video! I'm currently listening to Markov's chain class and you explaind stopping time very clearly. Thank you!

not all heros wear capes

Thank you great content!

Brilliant

Nice!

1:39

I gotta say your proofs are beautiful and make so much sense. Thank you very much! May God bless you!

I really like this proof. Thank you very much.

Provide proof of it

Very good sir🎉🎉🎉🎉 well explained I learned from u I am from Nepal

in the example at time stamp (15:13) you constructed intervals of the form (0, 1/n] but these intervals do not satisfy a_n > b_(n-1) condition you state above. it would be kind of you to clarify if i misunderstood what you are trying to state.

You are an agent of god sent on earth to explain conditional expectation to students who never had good teachers. This example cleared so many things, as you said in previous video "Think of the conditional expectation as an averaging over sets (or, equivalently, events) that are too fine for g to see inside."

you are awesome man. thank you uploading these videos.

If you are looking for a non-technical explanation of the 0-1 Law, you can find it here: th-cam.com/video/lopKqJwqk6M/w-d-xo.html

@Marton 13.47, definiton of expectation. Would it be accurate to summarize that if the Ai's are disjoint, then you can convert Ai's into Ai' s such that Ai' are disjoint and then use Ai' in the definition of the expectation?

Marton, sorry for troubling you again. Question: Difference between measurable and measure. Measure operates on elements of an algebra (domain). Measurable in the definition of the random variable operates on elements of omega - which are not elements of an algebra. Is this correct?

Marton, first off thanks so much for putting this online. Much appreciated. Question: Random variable X maps omega's to values in R. These values, produced by X as a map do not have to be less than 1. However, because it is in R, we can construct a Borel set for any value produced by X, find its inverse image (produced by X) and then apply the probability measure to it. So every time we have a probablity question about a value of X, it is really a probability question applied to the inverse image produced by X. Would this be an accurate summary?

I have a question Ingeneral Can I say that the union of A sub n is the supremum of all An ? And the intersection of A sub n is the infimum of An ?

you are the best teacher in this field. really thank you for your helping

Is there any relation between Lp convergence and a.s convergence at all?

U are a legend

Thank you so much. I was skeptical at first on how to integrate e^(quadratic) but now I know to substitute the integrals with constants

Are the variables xn+1 ... xn+m supposed to be independent variables, or can they be dependent also?

Our handwritten script looks almost the same 😁

Heloo can I ask you what this theorem helps us do?

In the definition of expectation, you used simple functions which had some measurable sets associated with them, the A_k's. Then you took a limit to find the expectation of nonsimple RVs. Won't the definition of expectation be dependent on these A_k's? How do you get around the fact that expectation definition might depend on the measurable sets in the definition of simple RVs?

At 12:30, E Z_n = E Z_{n-1} * m is the application of Wald's identity derived in FiTP25 (E(Z) = E(Y) * mu).

At 7:39, the form of mass function can be rewritten in a form of "negative Binomial coefficient" using the identity introduced in (just before) th-cam.com/video/NP9R7SxW7t4/w-d-xo.html (FTiP21/22. Generating function of Negative Binomial) The mass function of negative Binomial is Prob(X=k) = (k-1, r-1) q^{k-r} p^r, where (k-1, r-1) denotes the binomial coefficient of (k-1) choose (r-1). Define k = r + m, then the coefficient becomes (r+m-1, r-1) which equals to (-1)^m (-r, m). That means, if we define a pessimistic(?) negative Binomial random variable Y := X - r, so that Y measures the number of failures required to achieve r successes. Then, Y's mass probability function is Prob_Y(Y=m) = (-1)^m (-r, m) q^m p^r which is in a form of negative binomial coefficient and hence the name.

At 8:10, "X is proper, when Par(X<infty) = 1", where Par() denotes the partition function. I suppose this is the definition of a proper random variable. Then, if X is proper, the power series form of Par(s) is exactly the expectation E(s^X). It is then claimed that even if X is improper, as long as we consider 0<s<1, the summation form is equivalent to the expectation form of generating function. Could you please address a bit more on that? I feel like it has something to do with the contribution of X when X=infinity, but from the answer to my last question, that summation sum_{i=0}^infty actually does not contain X = infinity. So it looks like that that summation form is never equal to the expectation form as X = infinity is never considered in summation, regardless the value of s?

Thank you, the 2nd example really made something click for me.

At 8:00, why do we have Proba(Union_{i=0}^infty(X=i)) = Proba(X < infty)? I am confused as the left-hand-side is a union containing i = infty, but on the right-hand-side we only look at X<infty which explicitly excludes the infinity? At 8:35, 1 - sum_{i} p(i) = Proba(X=infty) is written down. Although the lower and upper limits of the summation is not explicitly written down, I guess they are 0 and infinity respectively. Then I am confused again why we have i = infinity on left-hand-side but we have Proba(X=infinity) on right-hand-side? I feel it is the same question and I lack background of something to understand this..

At 7:40, it is this proposition in the previous video used th-cam.com/video/UjNSGY_FKpI/w-d-xo.html

At 2:30, there should be no prime (denoting differentiation) on -exp(-y)?

At 1:00, from wiki it says that Huygens principle says that every point on a wavefront is itself the source of spherical wavelets. So I think Cau(b_x, a_x) * Cau(b_y, a_y) may be viewed as two consecutive projections and so the locations b_x, b_y and heights a_x, a_y add up intuitively. However, I am a bit confused as Cauchy distribution does not assume wave property of lights at all. How can it obey Huygens principle? By the way, looking forward to see complex function theory series on the channel.

At 6:51, it seems to say that the existence of odd moments is more tricky, why is so? What I can imagine about odd moments is that if the probability mass function is symmetric, then all odd moments vanish as the whole summand is an anti-symmetric function. But when it comes to the existence of limits I can hardly imagine the effect of odd n.

Proof part1) Start with a hedging strategy with portfolio including a stock (of that European option) and bond, we show that the initial value must be the value given by the theorem if we choose the probability p = (r-a)/(b-a). Proof part2) Start with the initial value specified by the theorem, we show that if p is chosen as (r-a)/(b-a), and Y_n is chosen as E(...|F_n) as in the lecture, we can find a hedging strategy. Q1. a little question: in proof part1), we define Y_n := (1+r)^{-n}X_n as the present value of the wealth on day n, because we start with an explicit hedging strategy (so can define Y_n in terms of X_n). But in the proof part2) th-cam.com/video/yQWUAqA4tzI/w-d-xo.html , when we write X_n = (1+r)^n Y_n, this is actually a definition of X_n, right? because the definition of Y_n comes first in part2), and then we define X_n = (1+r)^n Y_n so that we can apply calculation in part1) (and also lemma) to find H_n and hence A_n. But for this to make sense X_0 and X_N must match the values we want and that's the final step to check. Q2: is the probability space completely artificial? The result of the initial value x = (r+1)^{-N} E(S_N - K)^+ looks completely independent of a,b. However, p = (r-a)/(b-a) depends on a,b. Naively, it is not obvious if S_N depends on a,b. If b is close to r, I thought mean of S_N would be small compared with the case b>>r, as b is close to r means that stock is just a bit better than a bond when w_n=1. But I noticed later that in this case p approaches 1 as well so the stock is basically always in the "profitable state" (w_n=1). So is it true that once we decided a striking price (K) and number of days later (N), the value of the option is completely determined no matter what the underlying stock is? Thank you.

The definition of hedging requires that the wealth X_n is never negative during 0 <= n <= N. Though it may become clear after seeing the proof of the theorem in later videos, I am curious why do we need the condition X_n >= 0 for hedging? Naively, as long as the end result, i.e. the wealth on day N, X_N, equals to the value of the mixed stock+bond, we replicated the European option? Or is it required for the uniqueness property of the theorem?

Thank you so much for sharing such nice lecture series. It is my first time seeing a proof of the strong law of large number. It is enjoyable to watch the lectures paving the way to prove something which may be used often but never proven by many people. It all starts from reading somewhere that conditional expectation is a random variable not a number (which shocked me). Then I found and watched one of the MT course videos introducing conditional expectation and then I couldn't help but started from lecture 1 up to here (and will try to finish all). Really appreciated and hope the videos in this channel grows in the future.

A very basic question again.., I was trying to articulate what we learned in terms of the example of sequence of fair coin flips but confused. Consider fair coin flip, the probability space is (Omega, F, P), where Omega = {H, T} (i.e. head or tail), and sigma-algebra F = {0, {H}, {T}, Omega}. The random variable X maps H to 1 and T to -1. P(H) = P(T) = 1/2 for a fair coin. 1. When considering filtration, we need a process X_n, where each X_n is a fair coin random variable and hence they all map from the same Omega to {-1,1}. Then, F_0 = F_1 = ... = {0, {H}, {T}, Omega}. Q:The sigma algebras F_n do not get finer and finer because the independent fair coin flips do not accumulate the info? 2. Or, shall we define the probability space in a way that varies with n, Omega_n = {HH...H, HH...T, ..., TT..T }, where each element has exactly n factors of H or T, so the sample space is actually changing with the sequence index n? In this case, F_1 = {0, {H}, {T}, Omega} but F_2 = {0, {H}, {T}, {HH}, {HT}, {TH}, {TT},..., Omega}, where F_n looks finer and finer. However, the random variables X_n then has to be defined on Omega_n. The idea of 2. looks weird to me as we have been defining filtration with respect to a single fixed underlying probability space. But if 1. is true, then it looks like J_n = sigma(X_{n+1},...) = {0, {H}, {T}, Omega} = J, as every X_n contributes same terms to sigma algebra. This result is obviously wrong as P({H}) = 1/2 not equals to 0 or 1. How can I resolve this? Thank you.

For the identity at around 9:40, E(M_r ; F) = EE(M_r ; F | F_{r-1}) <= by Tower rule, = E(M_{r-1} ; F) <= by Martingale property. Notice that F is an element of F_n and so F is an element of F_{n+1}, ..., F_r too. This makes the condition on F and F_{r-1} "interchangeably". Iterate this process until we hit E(M_r ; F) = ... = E(M_n ; F). We cannot continue the iteration because F is not an element of F_{n-k} for k = 1,2,..,n. Just want to make sure that it is the property F in F_n which makes the iteration terminate at n, correct? thanks!

Another conceptual question.., C_n is said to be predictable if C_n if F_{n-1} measurable. The idea of this definition is that when making decision/strategy, we have only info up to (n-1) and no idea what happens at time n (and perhaps beyond). However, as we have filtration here, F_n is sigma-algebra in the increasing fashion in n. So if C_n is F_n measurable, it means C_n is F_{n+k} measurable as well for k=1,2,3,... I then have a question: In the definition of predictable/previsible random variable, is it OK that C_n take info up to a few steps before (n-1) but not really up to (n-1)? thanks!

Questions: 1. How to understand the superficially contradiction that F_n includes all info all to time step n (i.e. history) and event {T>n} (which looks like something happens in the future) should be also in F_n as a definition (i.e. complement must exist) of sigma algebra? Although {F_n} forms a filtration such that F_n gets finer and finer in n, so F_n indeed contains more info than F_m if n > m, as F_n is often constructed as the sigma algebra generated by random variables of X_k from 1 up to n. 2. Does T live in the same probability space as the random variables of the process, X_k, do? We start from a probability space (Omega, F, (F_n), P) with filtration (F_n). So all sigma algebras F_n are associated with the same sample space Omega. As for the random variable T, it takes values from 0,1,..,infty but what is the domain of T? It seems not to be Omega? I feel that if I understand 2. I may be able to resolve 1. but still struck.. thank you!

For eg2 at 12:50, an attempt to prove it raises two little questions.. 1. (adapted) let F_n = sigma(X_1, X_2,...,X_n), then X_1,...,X_n are F_n measurable and hence so is Prod_{k=1}^m X_k =: M_m, for m=1,...,n. This shows F is a filtration and M_n is adapted to F. 2. Since E(X_k)=1 is finite, E|X_k| is finite too. Then, E|M_n| = E|X_1X_2...X_n| <= Prod_{k=1}^n E|X_k| which is finite, where we used Holder's inequality with p=q=1. 3. E(M_n | F_{n-1}) = E(X_n M_{n-1} | F_{n-1}) = E(X_n|F_{n-1}) E(M_{n-1}F_{n-1}), where we used the independence assumption in the 2nd equality. From the independence assumption, E(X_n|F_m) = E(X_n) for n>m. So the 1st factor can be simplified as E(X_n|F_{n-1}) = E(X_n) = 1. From the adapted property 1., M_{n-1} is F_{n-1} measurable and hence 2nd factor = E(M_{n-1}F_{n-1}) = M_{n-1}. So we have martingale property. In the above, there are some gaps I couldn't close it yet: a) a product of random variables which is F-measurable is again F-measurable. Not sure if it is true? b) E(XY) = E(X)E(Y) given X,Y are two independent random variables. This is naively true using the independence property of probability, P(X,Y) = P(X)P(Y) and then thinking expectation as integral. But I am not sure how to prove it formally in terms of what we have in this series of course?

For eg1 at 11:35, I have a question in an attempt to prove it. 1. (adapted) let F_n = sigma(X1,X2,...,Xn), it is obviously a filtration. Then by construction M_k is Fn-measurable for k=1,2,..,n. Therefore, M_n is adapted to filtration. 2. (finite mean of absolute value for all n) E|M_n| <= E sum_{k=1}^n |X_k| = sum_{k=1}^n E|X_k|, where triangle inequality is used. The eg1 assumes zero mean of X_k but says nothing of E|X_k|, I have difficulty proving that E|X_k| < infty given E(X_k) = 0? 3. (Martingale condition) By the independence assumption and our choice of filtration, we have E(X_n | F_m) = 0 for n>m. Then, rewrite E(M_n | F_{n-1}) = E(M_{n-1} | F_{n-1}) + E(X_n | F_{n-1}), where linearity of expectation is used. For the 1st term on RHS, by adapted property, it equals to M_{n-1}. For the 2nd term on RHS, by independence property it equals to E(X_n) and then equals to zero by zero mean assumption. So we arrive at E(M_n | F_{n-1}) = M_{n-1}. How to complete step 2 (E|M_n| < infty for all n) ? Thank you!

A basic question regarding definition of script F_infty at 2:09. It seems we only defined sigma algebra generated by a random variable before but never defined a sigma algebra generated by unions of sigma algebras? In general, unions of sigma algebras do not need to be a sigma algebra. Then, how is sigma(unions of F_n) defined? Even if we can generate a sigma algebra from the unions, is it guaranteed to be unique?

At 8:23 when it talks about convergence almost surely, it is said that P(X_n -> X) = 1 is true for some set of Omega. Naively, I expected that all these convergence statements should be true for ALL elements of the sample space Omega? as random variables are functions on sample space? thank you!

In the monotone convergence theorem, how do we understand the effect of Y? say in part (a), Y looks like a kind of "lower bound", but since X_n is already converging to X in increasing fashion, the existence of Y looks redundant naively? although in the proof we will need Y so that we can apply the theorem of simple random variables to construct that set of sequences of simple random variables.

Questions: 1. What if for all n, it is always a fixed event A_K occurring? as it is true for all n, K could be only infinity. Is this scenario not making sense? but if it is possible then it's not infinitely many of A_k occur? 2. Do we need to impose an order on A_k here? from MT/2 Continuity of measure, the concept of limit on events exists only for increasing or decreasing A_k's. I am trying to understand the connection of limsup of events to limsup of functions. Here, the union piece looks like finding a sup (if increasing) from MT2 and then the intersection piece looks like taking a limit (if decreasing).

Could you elaborate a little bit on why E(X|g) is g-measurable? E(X|g) is a random variable and is hence a function from sample space to real line. A random variable is by definition measurable but I have difficulty understanding why this random variable E(X|g) is measurable with respect to g? Thank you.