
- 3
- 84 191
Computer Science Mathematics
เข้าร่วมเมื่อ 15 มิ.ย. 2014
Subsets and Power Sets
Examples of subsets and power sets.
More details at
peterolson.github.io/CS-Math/Lessons/Main.html?Set_Theory/Powerset
More details at
peterolson.github.io/CS-Math/Lessons/Main.html?Set_Theory/Powerset
มุมมอง: 5 324
วีดีโอ
Cardinality of Infinite Sets
มุมมอง 64K10 ปีที่แล้ว
Watch the video about cardinality of finite sets if you haven't already. th-cam.com/video/UEOeHUmvu7A/w-d-xo.html More details about cardinality of infinite sets at peterolson.github.io/CS-Math/Lessons/Main.html?Set_Theory/Cardinality_Infinite
Cardinality of Finite Sets
มุมมอง 15K10 ปีที่แล้ว
Explanation of cardinality for finite sets. More details at peterolson.github.io/CS-Math/Lessons/Main.html?Set_Theory/Cardinality_Finite


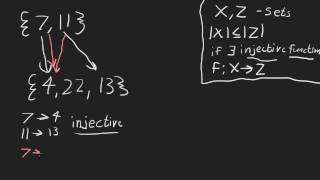
Where is the definition of cardinality?
Thanks, man. Very helpful.
Great, after watching dozens of videos, eventually I learned it. Thank you so much
Very clear & perfect Thxx
Sir natural numbers start from 1...not from 0 .... there are the whole numbers start from 0...so can you tell me why u are saying such sets ...THE SET OF NATURAL NUMBERS???
0 is a natural number. Integers don’t have a starting point.
@@paulu_ My book says they do start from 1. Why it has to be so confusing? Why isn't there a convention which states where N numbers starts from?
Unfortunately, different branches of mathematics differ on whether 0 is a natural number. In branches of math like logic, set theory, combinatorics, and abstract algebra, 0 is often considered to be a natural number. It is better for these disciplines when 0 is included in the set of natural numbers. In branches of math which use analysis/calculus, 0 is often not considered to be a natural number. It is better for these disciplines when 0 is not in the set of natural numbers (since they often want to take reciprocals of natural numbers, and 0 doesn't have a reciprocal). So that's how things typically go. In set theory and computer science, 0 is almost always considered a natural number.
0 is not a natural number. The set of natural numbers begins with 1.
It varies in maths, s0 no that’s not true
I UNDERSTAND THANK YOU
ℵ0
Finally!! I understood uncountably infinite set. It is very helpful. Thx
Now in a countable infinite set what is the state of "alef" when we take the set from 0 to minus infinity? What happens in the mapping then? Besides what if we count from minus to plus Infinity? What happens then?
What happens is one set is countably infinite and the other is uncountably infinite. That’s Cantor’s proof and he was the first to discover it. A genius.
(-infinity, 0) can be map with ℕ⨯ℕ By f(m,n)={-m/n : m∈ℕ, n∈ℕ} And ℕ⨯ℕ is countably infinite set . But it is only for set of rationals.
For further details visit this th-cam.com/video/JxhjURsOgkA/w-d-xo.html
thanks dude
Your video gives me the hope to continue study mathematics. Thanks
does the sequence have to be a 1 or 0 ? can it not takes any other values
They’re examples of countably and uncountably infinite sets. Cantor’s proof is the important thing not the examples of the sets chosen.
godlike explanation.
Excellent thank you sooo much
Excellent explanation and examples used to teach these concepts. Very helpful and thanks!
Good work You cleared my confusion regarding subsets...
Thanks!!!
Very helpful
0 belongs to the set of whole numbers. The set natural numbers/counting numbers includes 1,2,3,4 etc.
No shit Sherlock
God damn it, I have to know this material in 4 days from now for my set theory final :'(
saaaaaaame exactly same for me rn lmao
How'd it go?
please add more videos, your videos are good
very good
explained the complicated thing in a easy way, thank you
Hmm. I Don 't get it with the s'
thank you so much for this video! I finally understand uncountably infinite sets :D
you sound like bob from bob's burgers.......
😂😂😂
zero is not a natural number :(
It's debated, some argue that 0 is a natural number and a fair amount of computer scientists tend to be on the side of 0 being a natural number.
Zero is, together with one, the only "real" natural number. Everything else is mathematics and therefor abstractions. Either something is there, or it isn't. This requires an quantified space-time continuum though.
in discrete math 0 is considered as a natural number
it is natural number
Thats like debating someones point because they had a grammar error in their argument.
adn please let me more about math cause i need in highschool ok please
nice i want to learn that thing in high school thanks
thanks!
Thanks
But in the case where you take the power set of the set containing 1 and 2 you have only 3 elements(0, 1, 2) and not 2^2 elements?
aeroO bics 2^n is used for finding no of subsets not no. Of elements in a normal set...but since subsets are the elements of a power set therefore 2^n gives us the no. Of elements only in power sets ...so we need to keep in mind that if eg we have (1,2)
Its subsets are ((1),(2),(1,2),null set).so the formula applies here 2^n ..here n=2 therefore total subsets =4 and so are the total elements of the required power set
0 is not a natural number.
+Nakul Haridas This is highly debated in mathematics, and many see 0 as such.
I've watched all of your videos and saw that they were good.
really helpful!!! thank you