วีดีโอ

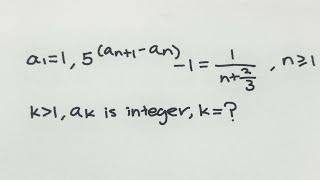
Amazing

3/4 h + h = 6..h = 24/7..area = .5*6*24/7 = 3*24/7= 72/7

Since the isosceles right triangle is in the middle, no matter the how you rotate that triangle inside, it will always be a quarter of the area of the square area of triangle=(hypotenuse^2/4) less (the area of square divided by 4) Atriangle=(32^2)/4 = 256 units^2 Aquartersquare=(21^2)/4 = 110.25 units^2 Ashaded=256 - 110.25 = 145.75

Nice explanation👍👍👍

0:53 whats the reason behind this

Can this be solved without using imaginary numbers? We know the sum of roots and product of roots. This could be substituted in the expansion of the expression provided.

wrong

a can also be equal to 300° and 420°, 660°, 780° and so on (also their negatives)

1/3

there is a symmetry and the result does not depend on "h=" in line 20: 10 print "reach the stars-math olympiad-geometry":dim x(1,2),y(1,2) 20 l1=2:l2=4:h=1.5:print "h="h:lh=sqr(l1^2-h^2):l3=sqr(l2^2-h^2)-lh 30 print "Das ergebnis BD*CD="; (2*lh+l3)*l3 40 x(0,0)=0:y(0,0)=0:x(0,1)=2*lh:y(0,1)=0:x(0,2)=lh:y(0,2)=h 50 x(1,0)=2*lh:y(1,0)=0:x(1,1)=2*lh+l3:y(1,1)=0:x(1,2)=lh:y(1,2)=h 60 masy=850/h:masx=1200/(2*lh+l3):if masx<masy then mass=masx else mass=masy 70 goto 100 80 xbu=x*mass:ybu=y*mass:return 90 line xba,yba,xbn,ybn:xba=xbn:yba=ybn:return 100 for a=0 to 1:x=x(a,0):y=y(a,0):gosub 80:xba=xbu:yba=ybu:for b=1 to 3:ib=b 110 if ib=3 then ib=0 120 x=x(a,ib):y=y(a,ib):gosub 80:xbn=xbu:ybn=ybu:gosub 90:next b:next a reach the stars-math olympiad-geometry h= 1.5 Das ergebnis BD*CD=12 > run in bbc basic sdl and hit ctrl tab to copy from the results window.

I don't like it. I think you should detele your channel

ich habe es mal vereinfacht und so gemacht wie in der lösung, weil ich sonst nie fertig geworden wäre: 10 print "reach the stars-q156|math olympiad|geometry|constructing squares" 20 dim x(4,2),y(4,2):wd=5:l1=21:l2=32:x(0,0)=l2/2:y(0,0)=l2/2:x(0,1)=l2 30 y(0,1)=0:x(0,2)=l2:y(0,2)=l2:x(1,0)=l2/2:y(1,0)=l2/2:x(1,1)=x(1,0)+l1/2 40 y(1,1)=y(1,0)-l1/2:x(1,2)=x(1,1):y(1,2)=y(1,1)+l1:nu=20:rem zahl der unterteilungen *** 50 wdu=90:xc=l2/2:yc=l2/2:for a=1 to 3:for b=0 to 2:xu=x(a,b):yu=y(a,b):gosub 60:goto 80 60 xvx=(xu-xc)*cos(rad(wdu)):xvy=(yu-yc)*sin(rad(wdu)):xv=xvx-xvy+xc 70 yvx=(xu-xc)*sin(rad(wdu)):yvy=(yu-yc)*cos(rad(wdu)):yv=yvx+yvy+yc:return 80 x(a+1,b)=xv:y(a+1,b)=yv:next b:next a:wdu=wd:for a=0 to 2:xu=x(0,a):yu=y(0,a):gosub 60 90 x(0,a)=xv:y(0,a)=yv:next a:rem den masstab berechnen *** 100 xmin=l2/2:ymin=l2/2:xmax=xmin:ymax=ymin:for a=0 to 3:for b=0 to 2 110 if x(a,b)<xmin then xmin=x(a,b) 120 if x(a,b)>xmax then xmax=x(a,b) 130 if y(a,b)<ymin then ymin=y(a,b) 140 if y(a,b)>ymax then ymax=y(a,b) 150 next b:next a:print xmin,"%",xmax:masx=1200/(xmax-xmin):masy=850/(ymax-ymin) 160 if masx<masy then mass=masx else mass=masy 170 goto 190 180 xbu=(x-xmin)*mass:ybu=(y-ymin)*mass:return 190 for a=0 to 4:x=x(a,0):y=y(a,0):gosub 180:xb1=xbu:yb1=ybu:x=x(a,1):y=y(a,1) 200 gosub 180:xb2=xbu:yb2=ybu:x=x(a,2):y=y(a,2):gosub 180:xb3=xbu:yb3=ybu 210 col=12:if a>0 then col=15 220 col2=12:if a>0 then col2=15 230 gcol col:move xb1,yb1:move xb2,yb2:plot85,xb3,yb3 240 gcol8:line xb1,yb1,xb2,yb2:line xb2,yb2,xb3,yb3:line xb3,yb3,xb1,yb1 250 next a:ages=(l2^2-l1^2)/4:print "die gesuchte flaeche=";ages reach the stars-q156|math olympiad|geometry|constructing squares 5.5% 33.3336071 die gesuchte flaeche=145.75 > ausführen mit bbc basic sdl und zum kopieren aus dem ergebnis fenster ctrl tab drücken.

Found max=8 and min =0.

GEAR 4th!!

Nice!

Welcome to Flat Earth.

Aren’t A,B,C,O concyclic here? 1:58

1:34 it can also be linked to similar triangles, great video as always 👍

Could you provide the complete question, I mean the statement?

Awesome solution. Just to show variety you can do it as well by connecting PC to get a diagonal of the square and then get it’s length by using this AP^2+PC^2=BP^2+PD^2 (can be proven by Pythagoras) and get PC = sqrt(3) then get the side of square and apply cosine rule on triangle APB

Thank you for the clear explanation and intreating problem

I think you missed a condition that a must be an integer, right?

a=24.

Replace x^2with x-1 to get instant soln

Follow up the following link if you want to solve grade 11 or o-level mathematics like a genius th-cam.com/video/YAM-A3vAXhk/w-d-xo.htmlsi=p_qOxs7SaHiezejV

Thanks for this video.But I want to ask something.q 's minimum value is not 16.q can be equal to 11.For exactly p=6 and q=11 5/11 < 6/11 < 4/7 If you look to this unequation , it is True. So why we don't take 11? Also I want to explain this solution: Please tell me if it is True or false. Firstly if these numbers are positive , we can multiply everywhere with 7q.So we will get 35<7p<4q , so p can be 6.And q can be 11 for the minimum value. (If these p,q are positive intigers.)

Great video! Though, how do you prove that y is in the interval from -1 to 1 (y z (-1;1))

Let <QCB=a=<PBA and side AB=BC=x x*sin a=6 (6+7)*cos a=x ->13*cos a*sin a=6 ->sin 2a=12/13 ->cos 2a=5/13 ->1-2*sin(a)^2=5/13 -> sin a=2/sqrt(13) x=6/sin a=3*sqrt(13) -> area(ABCD)=x*x=117

More easy with trigonometry!!!! Tg(DPC) = infinity = tg (CBA+DAB)

Bro this is Olympiad question I solved it in less than 5 seconds by seeing the thumbnail, wtf dawn easy, if this is Olympiad level than u will cry after seeing JEE advanced maths papers

471

because the three sides of dec triangle are a pithagoric tern

Great video, thanks. Can you explain why DEC angle is a right angle, thanks?

I am curious that whether the following solution is acceptable or not. Just give a number for the value of the function such as 1 for positive 1 we need x1 = 3 for negative 1 we need x2 = 3/2 then 1/3 + 2/3 = 1 same answer however I am not sure that it is accepted

f(x²+1) = x⁴ + 2x² - 3 f(x) ? ================ f(x²+1) = x⁴ + 2x² - 3 f(x²+1) = (x⁴ + 2x² + 1) - 4 f(x²+1) = (x²+1)² - 4 f(x) = x² - 4 1:49

van Aubel's theorem. AF/FD= 8/7 + 6/7=2

Why is the point M the circle of center?

why does the 5 cancel the log in base 5 ?

Knew answer in 5 seconds

cool solution

didn't understood a shit

It may not be obvious for some how you got from the x^2(y^2+1)+(y^2+1) step to (x^2+1)(y^2+1). You should also mention that the (y^2+1) multiplier was also factored out from both terms leaving (x^2+1). Just for clarity’s sake.

why does f(-x) the same as -f(x)? i want to learn but i cant grasp this part yet

The thumbnail does not match the video presentation. For those interested in the thumbnail's solution: g(x)=1/(1-x^2) and f(x)=x/(x^2-1)

This function is periodic over the integers with a period of 2. You can start evaluating f(6) to move forward to see a period of 2, and you can also move backward with a little more effort. The assumption is that this function is defined over the integers.

Cos(EBC)=Sin(ABE). S=5^2-0.5*3*4-0.5*3*5*(3/5).

how do you know the period is 6?

The value??

BX=40/sin(60°-a)sina,s=20√3/sin (60°-a) FZ=41(√3-1)-40/sin(60°-a) sina a=-arccos((163-41√3)/2/√(83 24-41*82√3)+arccos(-40/√(8324- 41*82√3)) 11896 285/1487× s=20√3/sin120°=40

{y=X²-4X,0=(x-2)⁴-12(x-2)²-(x-2)+32; (z-2)³-17 3/4(z-2)-27 33/64=0 z=2+(880 1/2+√(1761²-71³*256/2 7)/2)¹/³/4+(..-..)..;2-(880 1/2+√ (1761²-71³*256/27)/2)¹/³/8-(..-..)..±√(3/4((880 1/2+√(1761²-71³*25 6/27)/2)¹/³/4+(..-..)..)²-17,75)i