
- 11
- 352 023
jHan
United States
เข้าร่วมเมื่อ 10 ม.ค. 2021
Mathematics can sometimes be frustrating and unintuitive. This channel seeks to explain and express mathematical concepts and ideas in a beautiful, intuitive way. Animations are made with 3Blue1Brown's animation engine Manim: github.com/3b1b/manim
How to Construct Infinite Sets
What are the natural numbers? The integers? The rationals? The reals? While we may have an intuitive understanding of these numbers and sets, it is not so easy to actually construct these sets formally. To do so, we must use some axioms of set theory, and using only these assumptions, formally describe what these infinite sets should look like. We will develop various tools in set theory, like ordered pairs, relations, ordering, and equivalence classes, to begin with only zero, and from nothing, build all of the real numbers.
0:00 Introduction
1:46 Set Theory and Basic Notions
8:13 Axiom of Infinity and the Naturals
13:09 The Integers
23:19 The Rationals
26:00 The Reals
36:38 Conclusion
Additional Resources:
Wikipedia article on the Construction of the naturals: en.wikipedia.org/w/index.php?title=Natural_number#Set-theoretic_definition
Wikipedia article on the Construction of the Reals: en.wikipedia.org/wiki/Construction_of_the_real_numbers
Wikipedia article on ZFC: en.wikipedia.org/wiki/Zermelo-Fraenkel_set_theory
Axiom of Choice video: th-cam.com/video/szfsGJ_PGQ0/w-d-xo.html
Cardinality of the Continuum video: th-cam.com/video/iaUwNuaSLUk/w-d-xo.html
Music:
c418.bandcamp.com/album/dief
Imaginary Interlude by C418
c418.bandcamp.com/album/circle
minimal by C418
love by C418
patriciataxxon.bandcamp.com/album/crocus
Crocus 2 by Patricia Taxxon
Far the Days Come by Letter Box
------------------------------------------------------------------------------------------------
Animations were made by Manim, an open-source python-based animation program by 3Blue1Brown.
github.com/3b1b/manim
This video was submitted to 3Blue1Brown's SoMEπ (Summer of Math Exposition Community Edition).
some.3b1b.co/
0:00 Introduction
1:46 Set Theory and Basic Notions
8:13 Axiom of Infinity and the Naturals
13:09 The Integers
23:19 The Rationals
26:00 The Reals
36:38 Conclusion
Additional Resources:
Wikipedia article on the Construction of the naturals: en.wikipedia.org/w/index.php?title=Natural_number#Set-theoretic_definition
Wikipedia article on the Construction of the Reals: en.wikipedia.org/wiki/Construction_of_the_real_numbers
Wikipedia article on ZFC: en.wikipedia.org/wiki/Zermelo-Fraenkel_set_theory
Axiom of Choice video: th-cam.com/video/szfsGJ_PGQ0/w-d-xo.html
Cardinality of the Continuum video: th-cam.com/video/iaUwNuaSLUk/w-d-xo.html
Music:
c418.bandcamp.com/album/dief
Imaginary Interlude by C418
c418.bandcamp.com/album/circle
minimal by C418
love by C418
patriciataxxon.bandcamp.com/album/crocus
Crocus 2 by Patricia Taxxon
Far the Days Come by Letter Box
------------------------------------------------------------------------------------------------
Animations were made by Manim, an open-source python-based animation program by 3Blue1Brown.
github.com/3b1b/manim
This video was submitted to 3Blue1Brown's SoMEπ (Summer of Math Exposition Community Edition).
some.3b1b.co/
มุมมอง: 5 814
วีดีโอ
The Axiom of Choice
มุมมอง 104K8 หลายเดือนก่อน
Mathematics is based on a foundation of axioms, or assumptions. One of the most important and widely-used set of axioms is called Zermelo-Fraenkel set theory with the Axiom of Choice, or ZFC. These axioms define what a set is, which are fundamental objects in mathematics. And the Axiom of Choice is arguably one of the most important and interesting axioms of ZFC. But what does it really say? An...
Genius Mathematicians Lost Too Soon
มุมมอง 3.6Kปีที่แล้ว
Some mathematicians changed the field of mathematics at a young age, only to die too early. Let us look at the lives of some of these young, brilliant minds who left too soon. Evariste Galois was a French mathematician who laid the foundations of abstract algebra and Galois theory, proving the quintic's insolubility. Srinivasa Ramanujan was an Indian mathematician who, upon his genius being dis...
But what is a Vector Space?
มุมมอง 3.8Kปีที่แล้ว
Vectors are fundamental tools in mathematics and sciences. Yet different fields like mathematics, physics, and engineering seem to define vectors differently. It is mathematics, unsurprisingly, that formally defines a vector. We will go through this process of formalization, using the foundational tools of abstract algebra to define and construct a vector space. Additional Resources: Wikipedia ...
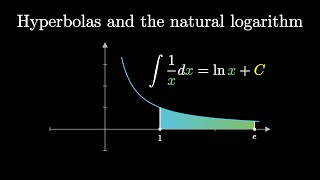
Why Logarithms Appear in This Integral
มุมมอง 2.9Kปีที่แล้ว
Before the days of Calculus, one Pierre de Fermat wanted to find the area under the function f(x)=x^n. This problem we now call "integration" was then called "quadrature" or "squaring". Fermat was able to square every function f(x)=x^n for any rational n except for one case: n=-1 (that is, the hyperbola). It turns out that this unique nature of the hyperbola was tied to logarithms and Euler's n...
How to Find the Biggest Primes
มุมมอง 11K2 ปีที่แล้ว
How do people find big primes? These primes have millions of digits, and may take years of collective effort and computing power to be found. Unsurprisingly, mathematicians have figured out various ways to more efficiently and accurately find these big primes. In the process, the unique and interesting properties of various primes have also been found. Great Internet Mersenne Prime Search: www....
Cardinality of the Continuum
มุมมอง 60K2 ปีที่แล้ว
What is infinity? Can there be different sizes of infinity? Surprisingly, the answer is yes. In fact, there are many different ways to make bigger infinite sets. In this video, a few different sets of infinities will be explored, including their surprising differences and even more surprising similarities. 0:00 - Euclid's Proof of Infinite Primes 1:55 - Bigger Infinities? 2:27 - Set Theory and ...
The Cardinality of an Interval
มุมมอง 3.3K2 ปีที่แล้ว
Cantor's Diagonal Argument proves that there are an uncountable number of real numbers. But what about any interval of real numbers? Are those sets uncountable as well, no matter how small the interval?
Can the power of two irrationals be rational?
มุมมอง 4.6K3 ปีที่แล้ว
Are there two irrational numbers, let’s say x and y, such that x to the y is rational? The answer to this question brings us through a fascinating journey about transcendental numbers and the Gelfond-Schneider theorem. Additional Resources: Where I found this theorem: math.stackexchange.com/questions/728223/simple-beautiful-math-proof/728276 Music: www.purple-planet.com Animations were made by ...
Why do trig functions appear in Euler's formula?
มุมมอง 150K3 ปีที่แล้ว
Why do trig functions appear in Euler’s formula? This was the question I had when I first saw Euler’s formula. This connection between trigonometry and exponents seems so unexpected, especially along with complex numbers. To answer this question, we must journey into the intricate and beautiful mathematical relationship between trig functions, e, and complex numbers. We will look at two differe...








The comtinuum is 1. A single unit. 1 + 1 + 1 + 1 + 1... = 1 = N = R. Numbers have relative values, they are ratios of an single unit. 1 + 1 + 1 + 1 = 4. Each 1 have a value of 1/4, 1 € N. N = R = C in 1. This because every real number can be expressed as an inverse of 1 times an multiple of 1. 0.5 x 2= 1, 0.25 x 4= 1. Every number can be expresed as an ratio of 1. That means 2 is 2/1 when the value of the 2 individual units is 1/2. Natural and real numbers have relative values. Numbers come from a single UNIT.
The cyclical nature of these functions is beautiful. If you’ve ever done an integration by parts problem with a trig function it’ll start to cycle if you don’t stop it early. Also the way I remember derivatives and integrals of sin and cos is with four quadrants. sin -cos cos -sin If you move clockwise on the wheel it gives you the derivative. If you move counterclockwise, the integral
Awesome video!
Amazing video on the topic.
Mmmrrmm yesss the nOnEmPtY set has eLeMeNtS that i can pick!!
You are doing a great job unpacking so much in this video. I need to watch it again to absorb more if it.
big W for your vid and yt career, you remind me of vsause but more formal but still introductionary like him, im studying math rn and this vid is actually good quality
that's amazing
The problem I have with the diagonal method is that the same method can be used to show any partial set of whole numbers is incomplete.
Zorns Lemma
Excellent breakdown and video here. also/and the outro commentary of these concepts - master class. ty
This video was amazing!
realy good vidéo, thank you
We would like to know more about Yutaka Taniyama
means e^-1 =-1 is wrong and π must=0
How many degrees is X?🤔
0=(0,0)
e^√-1*π+1≠0 0=(x,y), it means x 0, y0
cos(0)+isin(0)=0 but it isn't equal really 0
Background noise (drum) is very annoying.
That was magical...simple and elegant!
Music on the background is very disturbing
an axiom that does crazy stuff
Euler and Guass were the greatest mathematicians to ever live respective to their time
Thank you for this video! I understand the AoC much better after watching it. It's fascinating to see how thoroughly set theory is connected with other branches of mathematics. The visuals and audio were fantastic, and you explained things at exactly the right level for me (2nd year undergrad). I feel like I've just watched a very strong lecture at my university. Subscribed :)
4:22 Bernays
talk tuah
poopy fart head
i spent a day trying to prove this with the taylor series, still my most enjoyable day in terms of math
Amazing video, Physics major and we use this all the time, now I have a much more intuitive understanding of the Euler's formula
I am familiar with Dedekind Cut a few years back. But this is the first time I learned the rationale behind the rationals.
A whole series of videos of ZFC like this will surely go viral.
2^136279841-1, new largest known prime, discovered Oct 12 2024
In a university study you would expect a more precise language. You would hear Euclid's proof explained as "there are infinitely many primes", as in, not just finitely many primes. Rather than "there is an infinite number of primes", easily misunderstood as if to say there is a certain number of primes, and that number is infinite. This only becomes meaningful once you also realize that there is a set the elements of which are exactly the primes, and this set has a certain cardinality, and that cardinality is infinite.
Thanks! This really helped
im gonna try and find the biggest perfect number i can fathom Day 1: 137438691328
I started gasping and lighting screaming when i saw the end of the taylor series proof. Im bewildered
That proof is wrong. Taylor series are valid for real integers, not marvel universe numbers like i*x.
@pelasgeuspelasgeus4634 *bigger gasp*
@@Founder2721 meaning?
I love this
Great video, it's so hard to find maths content that isnt either not related to what you want to find or just incredibly complicated.
This video is pointless since euler formula is simply wrong. Left side is exp function which ranges from 1 to infinity. Right side is the sum of 2 trig functions each ranging from -1 to 1. So, how can these sides ever be equal? Stop parotting, start thinking.
what's your book there?
You deserve more subscribers, amazing explanation loved it.
The game.
amazing man! subscribed
22:50 I almost immediately think, why can't the reals be ordered like you do with the integers? Compare the absolutes of two numbers, and give the priority to the positive should their absolutes be equal. Unless of course, you are talking about Dedekind cuts.
Okay, surely you can do that; but that's not a well-ordering relation, because not every set has a minimum. Consider an open interval from 0 to 1; it can be seen that re-ordering negative numbers doesn't change anything. What's the minimum of this set? 1/10? But 1/100 is closer to zero. 1/1000 is even closer. And so on; for any positive number x there is one closer to zero, such as x/2. The infimum of this set is of course 0 (any set bounded from below has one); but that's not a minimum because it's not an element of the open interval. In fact, a well-ordering relation on real numbers can't be constructed in the usual sense; no formula can be proven to define one (in the sense that there exists exactly one set satisfying that formula and that set is a well-ordering of real numbers). The existence of such a well-ordering is a consequence of axiom of choice; without axiom of choice it's consistent that real numbers can't be well-ordered.
Thanks for the video really helpful for my university class.
This is a perfect video! I just have one question: why is natural number to the power of natural number the set of all positive integer functions? Can someone please explain it for me😢
Ratke Spurs
Amazing video but I still have one question. Like how do you classify e^ix as imaginary or real? Like for imaginary i must be multiplied to the number and for real no i at all. But this e^ix has i in the exponent, so I got confused at this part.
Is that the only thing confusing you? How about the fact that one side (exp function) goes from 1 to inf while the other side (sum of 2 trig functions) is obviously finite? How can they be equal?
14:46 wouldn't the domain be a subset of the power set of X? if x belongs to a particular Xy_1 it cant belong to any other such Xy_2 so the domain would be like disjoint subsets of X?
17:00 The musical choice is fantastic! It truly whisper the idea of "there's some powerful concept here to be grasped, but it's doomed indeed". Genius! Also, the part immediately preceding it has got a VERY inspiring music, which lift the spirit to the idea of "this concept is very powerful, harnessing the power and patience of infinity to gain the ability to be exact"! (17:00 _unless_ ... *there's a hole** ) also, the ending speech and the "almost pun" is ... delightful! I love it!