วีดีโอ

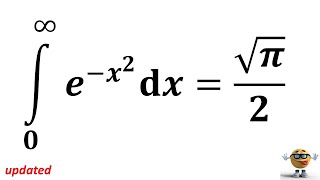
Evaluating for entrance exam not too much worthy instead we have to use the short trick

Can it be solved using I(t) = int 0->1 (integrand * e^-tln(x)) dx? I(0) equals the initial integral and I’(t) = int 0-1 (x^2 - 1)t*(e^ln(x))^-t) dx = int 0-1 (x^2 - 1)t*x^-t dx? That is where i get stuck

سبحان الله العظيم❤ سبحان الخالق❤ سبحان المصور القهار❤ سبحانالودود اللطيف ❤ سبحان الهادي الكريم❤

سبحان الله العظيم❤ سبحان الخالق❤ سبحان المصور القهار❤ سبحانالودود اللطيف ❤ سبحان الهادي الكريم❤

I believe this is incorrect, you might have left out a factor of 1/(a^5/2) in the final answer

Your video is great!! It helped me lots. Thanks man.

How can I get the code from vpython

Does K means Kc or Kp? Either WAY?

Does K means Kc or Kp? Either WAY?

Amazing

Answer is right but I didn't understand this method 😢😢😢

But du Ka kya hua😢

Nice 😊

how did you make this simulation

thanks man keep this series up. will for sure tune in

Sir how to integrate 1/√2π integral 2 to infinity e^-t^2/2 dt

Thank you

❤❤❤❤

Sigma 🗿🗿🗿🗿🗿

You are a lil bit fast 😢

Nice broo

Can you use the rule of odd functions for infinite bounds?

And suddenly pi pops out. No circles in sight.

This can also be done with Feynman's trick (differentiation under the integral sign). We use the Gaussian integral, slightly modified in this case as we instead integrate e^{-\alpha x^2} dx, a u-sub removes the alpha from the integrand (with alpha>0) and we evaluate using the Gaussian integral result, leaving a function of alpha. On the other hand, differentiating this integral wrt alpha gives the desired solution (with a minus sign) after setting alpha=1. Differentiate the function of alpha and evaluate at 1, fixing the sign and we are done.

Excellent, I was unable to understand why we used product rule instead of quotient rule, but now it's clear

8:12 - Am I the only one who heard a woman's voice ?

Amazing man , I was also stuck in this problem And can not understand what i was doing wrong You explained very well ❤❤

I really like the explaination and overall video style! Keep going. I also have a really fun one: ∫{-∞,∞}cosⁿ(x)/(x²+1)dx (n∈N). Or at least it was fun for me.

God Bless you sir🙏

Thanks, brother.Take love

Thank you so much <3

yes yes yes

🥰🥰

😍😍

u are super genius terry 😍😍

Amazing !

Minor correction "anything to the power 0" is not 1. not if the anything is 0.

Hi sir, which software do you use to record your videos?

i love you

this is great stuff! i hope you can derive the physics of a pendulum without the typical derivation of sin theta ~ theta. in other words, the bessel functions of the first and second kinds and how to derive the constants

Just substitute x^2=t. Differentiate and rearrange to get a form of Gamma function. Evaluate it by standard values. Simple.

Good stuff

thank you for the video! keep up the good work :)

This is the best. It is so clear because no step is skipped nor glossed over compared to other derivations.

but my book formula is Change of U= Q-W

Thank you so much!!

00:50 brilliant video however one thing I do not understand is why you are evaluating sin(theta) and cos(theta) at pi/2 ? because isn't the integral going to infinity? thanks. otherwise great video keep it up

cosx is d(sinx)/dx so (sinx)^2/2+C

You helped me in thermodynamics and now in the Integrals I'm encountering in quantum mechanics. Thank you so much for this detailed version....loved the volume under integral explanation

Just to let you know, trig sub is normally a term used when changing from cartesian to polar coordinates, or when you substitute u to be a trigonometric function. It can be used for example in integrals like sqrt(1-x^2), where you take sin(t)=x, so t=arcsin(x) and get an easier integral to solve because sqrt(1-x^2) is now cos(t). And we get in this case the integral of cos(t)^2. What you did is just usage of the sum of angles formula for sin, and simple substitution when taking u=2x