
- 199
- 433 210
Fertig Research Group: Multiscale Failure of Materials
United States
เข้าร่วมเมื่อ 19 ธ.ค. 2013
Material Fracture (Ductile vs. Brittle Fracture)
Introduces ductile and brittle fracture. Describes the macroscopic appearance of both types of cracking. Describes the microscopic mechanism that are responsible for each type. Briefly covers fractography and shows cup-and-cone fracture for ductile materials and chevron markings for brittle materials. Introduces the ductile to brittle transition. Gives example of Liberty Cargo Ships in WWII.
มุมมอง: 2 754
วีดีโอ
Material Fracture (Theoretical Fracture Strength)
มุมมอง 1K2 ปีที่แล้ว
Introduces the idea of fracture as the creation of two new surfaces. Develops the idea of theoretical fracture strength on the basis of elastic modulus, lattice spacing, and surface energy.
Linear Elastic Constitutive Behavior: Hooke's Law
มุมมอง 8712 ปีที่แล้ว
Develops a linear elastic constitutive law in both tensor notation and Voight notation. Gives the form of the compliance matrix for an orthotropic material.
Review of Strain: (Definition of Small Strain Tensor)
มุมมอง 8502 ปีที่แล้ว
Defines the small strain tensor in terms of displacement gradients. Shows how this intuitively yields the same solution as the simple change in length divided by original length.
Review of Strain: Types of Deformation
มุมมอง 4462 ปีที่แล้ว
Shows how strain tensor can be used to compute changes in length, changes in angle, and changes in volume leading to normal engineering strain, engineering shear strain, and volumetric strain, respectively.
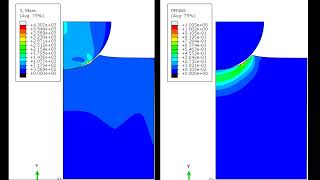
Simulated Rockwell B Hardness Test for 1018 Steel
มุมมอง 1.2K2 ปีที่แล้ว
This is an axisymmetric simulation in Abaqus of a Rockwell B hardness test with material properties that are nominally 1018 Steel. The left-hand animation shows the von Mises stress evolution; the right-hand animation shows the plastic strain magnitude.
Variational Principles of Elasticity (Principle of Virtual Work)
มุมมอง 1.8K2 ปีที่แล้ว
Develops the Principle of Virtual Work from the idea of work done by virtual displacements. Demonstrates that the Principle of Virtual Work is an equivalent statement to the equations of equilibrium.
Variational Methods (Parametric Representations)
มุมมอง 3092 ปีที่แล้ว
Expands the discussion of optimization of functionals to include parametric representations so that functions need not be single-valued. Shows that any solution (even a non-single-valued function like a circle) that satisfies the conventional Euler-Lagrange equation is a valid extremizing function.
Variational Methods (Finite Constraints - Geodesics Example)
มุมมอง 3572 ปีที่แล้ว
Develops the solution of a simple geodesic optimization in 3D where the curve length to be minimized lies on a sphere centered at the origin. The solution ultimately shows that the optimized path lies at the intersection of the sphere and a plane through the origin, which leads to solution that is a great circle of the sphere.
Variational Methods (Finite and Differential Constraints)
มุมมอง 6642 ปีที่แล้ว
Develops the methodology to optimize a functional subject to finite equation constraints and differential equation constraints. Introduces the concept of a Lagrange multiplier function. Shows how to create an auxiliary functional that can be optimized to yield the Euler-Lagrange equations.
Variational Methods (Isoperimetric Example)
มุมมอง 3612 ปีที่แล้ว
Develops the solution to an example of extremizing (maximizing) the area under the curve subject to the constraint that the curve be of some fixed length L. Uses Lagrange multipliers to form an augmented functional from the constraint functional and shows how to compute the solution.
Variational Methods (Ritz Method and Finite Element Analysis)
มุมมอง 3.2K3 ปีที่แล้ว
Begins with the total potential energy for an elastic body and uses the Ritz method to develop the governing system of matrix equations for FEA. It returns the identical result to the methods that were developed previously by solving the equations of motion in their weak form.
Variational Methods (Rayleigh-Ritz Method)
มุมมอง 9K3 ปีที่แล้ว
Develops the Rayleigh-Ritz method for approximating functionals. Shows how extremization of a functional can be reduced to extremization of a function. Goes through an example problem developing a 1-term Ritz solution to an example functional.
Variational Methods (Potential Energy of an Elastic Body)
มุมมอง 1.6K3 ปีที่แล้ว
Develops the functional describing the potential energy of an elastic body. Demonstrates that extremizing this functional to get the stationary potential energy yields the Principle of Virtual Work, which is the weak form of the equations of equilibrium. Thus, the lecture validates using the extremization of the potential energy functional for solving for elastic solutions.
Variational Methods (Principle of Stationary Total Potential Energy)
มุมมอง 2.5K3 ปีที่แล้ว
Defines the Principle of Stationary Total Potential Energy. Gives a simple example for its use with a linear spring under axial load. Discusses strain energy potential and potential energy due to applied loading.
Variational Methods (Functionals with Multiple Independent Variables)
มุมมอง 1.1K3 ปีที่แล้ว
Variational Methods (Functionals with Multiple Independent Variables)
Variational Methods (Functionals with Multiple Dependent Variables)
มุมมอง 1.1K3 ปีที่แล้ว
Variational Methods (Functionals with Multiple Dependent Variables)
Variational Methods (Functionals with Higher Order Derivatives)
มุมมอง 1.4K3 ปีที่แล้ว
Variational Methods (Functionals with Higher Order Derivatives)
Variational Methods (Natural Boundary Conditions)
มุมมอง 2.5K3 ปีที่แล้ว
Variational Methods (Natural Boundary Conditions)
Variational Methods (First Integrals of the Euler-Lagrange Equation)
มุมมอง 1.8K3 ปีที่แล้ว
Variational Methods (First Integrals of the Euler-Lagrange Equation)
Variational Methods (Example - Surface of Revolution)
มุมมอง 6313 ปีที่แล้ว
Variational Methods (Example - Surface of Revolution)
Variational Methods (Example - Shortest Path)
มุมมอง 8813 ปีที่แล้ว
Variational Methods (Example - Shortest Path)
Variational Methods (Fundamental Lemma of Variational Calculus)
มุมมอง 2.5K3 ปีที่แล้ว
Variational Methods (Fundamental Lemma of Variational Calculus)
Variational Methods (Functionals and Extremization)
มุมมอง 3K3 ปีที่แล้ว
Variational Methods (Functionals and Extremization)
4-4: Dynamic FEA (Mode Superposition - Modal Analysis)
มุมมอง 1.4K3 ปีที่แล้ว
4-4: Dynamic FEA (Mode Superposition - Modal Analysis)
4-2: Dynamic FEA (Newmark-beta Implicit Integration)
มุมมอง 4.2K3 ปีที่แล้ว
4-2: Dynamic FEA (Newmark-beta Implicit Integration)
4-1: Dynamic Finite Element Analysis (Natural Frequencies and Mode Shapes)
มุมมอง 3.2K3 ปีที่แล้ว
4-1: Dynamic Finite Element Analysis (Natural Frequencies and Mode Shapes)
3-3: Nonlinear Finite Elements in 3-D (Updated Lagrangian Formulation)
มุมมอง 9613 ปีที่แล้ว
3-3: Nonlinear Finite Elements in 3-D (Updated Lagrangian Formulation)








7:40 that beta tantalum is SUS
Thank you for such an excellent explanation. However, in eqn 9, the velocity term may need to be reorganized by deleting dt from the denominator?
thank you so much for this video! i was struggling to understand how to get the wt% but now its clear!
5:35 should be V_j instead of V_K
If humanity vanished today, how long until the steel we have made is unrecognizable? In 10 thousand years would you be able to tell it was a truck or would it just be ore?
Thanks man, still very helpful.
what is the reason of high melting temperature to about 251c in PET amorhous Is that any relation tm and IPA
Hi Prof. Fertig, what textbooks do you recommend? May I have lecture notes?
What textbooks do you suggest for this course?
how am I an undergraduate student but I'm here
thanks, the course is well equipped with required concepts
Hi professor, I really appreciate these awesome lectures. I have a quick question. Isn't structural steel after peaking in capacity a softening material as well? Steel first strain harden and the reaches a maximum stress after which it have a negative slope which makes unstable as well, how do we approach that from plasticity perspective? Thank you so much in advance
At time 05:10 in the video it seems like the closed interval [ \zeta - \delta, \zeta + \delta ] should be an open interval ( \zeta - \delta, \zeta + \delta ) since \psi(x) > 0 at the two end points. To me it appears to break the continuity of \psi(x) at the endpoint whereas if this was an open interval it would be OK because \psi would equal zero at the endpoints and when you are in the interior of the open interval then \psi would approach zero as you get closer to the endpoints? Thanks for the great video series!
Thank you for this series of courses.
Thank you!!! Great video professor.
👏😮
This video saved me from going in wrong pathway. Thanks a lot!
when we say momentum, it has the unit of m*v, right? In this video, why does the momentum equation have a different unit?
You said, conventional calculus is used to extremize function and variational calculus is used to extermize Functional. The function returned in calculus of variation is minimum at every point in the domain OR does the minimum is in average sense due to fact we integrate the functional in domain?
Thank you!!!!
You're welcome!
kms
Sir, the meaning of zi and X is not clear yet. Could you suggest few resources to get clarity on their meanings. Thanks!
Thanks Dr. Fertig.
If the point just on the blodfaced line bondary, does this mean the coexistence of the phases involved?
Thanks Dr. Fertig.
Thank you Dr. Fertig! I am able to follow the lecture.
10:05 can we dot product with e'_l instead of e'_n. In this way, no need the kronecker delta.
7:25 it should be R_ij * R_kj, right?
9:47 should be "n dependent variables u". Right?
Great lecture
I watched the video and completely understood. Thanks
I see you have shown many derivations, so one get good understanding of basics. Do you have some class notes or recommended book that follow exactly like your covered the entire topics of fea.
You showed only a single graph for which there is a variation, which we derived. Since in this and in previous case (of last videos based o derivatives) we want to find an extremal function, which will have an infinite number of 'points' along x axis. My question is about eta function we used previously and referred here as well. Do we will need an infinite number of eta functions for each point x for comparison with 'known' assumed function. This will also imply that we will have to make similar calculation for infinite number of x axis points. Am i correct?
I last part of lecture, one see that 1-c1 in sqaure root. We generalized this to A. Would not value to c1 have any constraint on choices of values of c1or A in final u?
I was wondering the same thing. Aren’t we restricting c1 to be less than 1…?
Nevermind I see. c1 is equal to sqrt(2)/2. This is because if A = 1, then u’ = 1 and then you can solve for c1. Lol!
What would happen if you were to cool to 400 degrees and wait until you have 50% bainite, and then quench to room temperature? What would the microstructure be?
thank you for this video. Is it possible to implement this without the stiffness matrix, but with the internal force vector Fint(u_(k+1)) ? The factorazation does not work like this to solve for u_(k+1) in the last step
Thank you for interesting video. If we put (6) into (4), we get negative value of pi (if displacement and force have same direction). It's a little bit confusing. Potential energy is negative at equilibrium? Could you please comment, why this happens?
Nice lecture and explanations
Thanks and welcome
Hi, Professor. Any recommended textbook for learning variational of calculus?
TQ
Please suggest reading text for this topic
www.amazon.com/Materials-Science-Engineering-William-Callister/dp/1118324579/ref=monarch_sidesheet
172/27
Sir, @ 8:58 how do we compute the internal resistance at n = 0
Wow, our continuum mechanics professor had given this expression to prove in the final exam when I was in my first year PG. Now I understand!! Thanks and Cheers!
Which software did you use
Abaqus
Prof. kindly tell the book you are using as reference.
This is so clear thank you. If energy lost/energy stored = 4 x pi x tan delta, doesn't this imply virtually all energy is lost in vulcanised rubber, where tan delta is around 0.1 at room temperature?
excellent demonstration
Thank you! Cheers!
Thank you so much for spending time on these high quality lectures. I have learnt a lot from these.
Great lecture, Could you tell me the textbook you uesd, Thanks a lot.