
- 214
- 53 550
Project Patimo
เข้าร่วมเมื่อ 14 พ.ค. 2016
The goal for this channel is to help students by offering a free point of view on certain topics and problems.
If you notice a mistake, comment under the videos. If you want to contribute by sending in your videos (you will be credited) let me know.
If you notice a mistake, comment under the videos. If you want to contribute by sending in your videos (you will be credited) let me know.
Ex 12.7-11 Space Flight Dynamics Craig A. Kluever
An axisymmetric satellite has principal moments of inertia I1 = I2 = 240 kg m 2 and I3 = 80 kg-m 2.At time t = 0, the satellite has angular velocity ω0 = 0.9u3 rad/s as expressed in 123 body-frame coordinates. The satellite has flexible antennas that dissipate energy over time. Determine if the following angular velocity vectors at arbitrary time t = t1 represent a feasible solution to torque-free motion. Explain your answers.
a) ω(t1 ) = 0.051262u1 + 0.034882u2 + 0.870288u3 rad/s
b) ω(t1 ) = 0.1u2 + 0.848528u3 rad/s
c) ω(t1 ) = 0.245746u1 + 0.172073u2 rad/s.
Problems 12.7-12.11 involve the torque-free motion of an axisymmetric rigid satellite. The satellite’s moments of inertia about the 123 principal axes are I1 = I2 = 150 kg-m2 and I3 = 30 kg-m2, and the 3-axis spin rate is ω3 = 0.6 rad/s. Figure P12.7 shows the 1- and 2-axis angular velocity components for the torque-free motion.
12.7 Determine the nutation angle θ.
12.8 Determine the angle γ between u3 and ω.
12.9 Determine the precession rate ψ (in deg/s).
12.10 Determine the Euler angle rate φ (in deg/s).
12.11 Determine the Euler angle φ at time t = 0.
a) ω(t1 ) = 0.051262u1 + 0.034882u2 + 0.870288u3 rad/s
b) ω(t1 ) = 0.1u2 + 0.848528u3 rad/s
c) ω(t1 ) = 0.245746u1 + 0.172073u2 rad/s.
Problems 12.7-12.11 involve the torque-free motion of an axisymmetric rigid satellite. The satellite’s moments of inertia about the 123 principal axes are I1 = I2 = 150 kg-m2 and I3 = 30 kg-m2, and the 3-axis spin rate is ω3 = 0.6 rad/s. Figure P12.7 shows the 1- and 2-axis angular velocity components for the torque-free motion.
12.7 Determine the nutation angle θ.
12.8 Determine the angle γ between u3 and ω.
12.9 Determine the precession rate ψ (in deg/s).
12.10 Determine the Euler angle rate φ (in deg/s).
12.11 Determine the Euler angle φ at time t = 0.
มุมมอง: 44
วีดีโอ
Ex 12.5 Space Flight Dynamics Craig A. Kluever
มุมมอง 2412 ชั่วโมงที่ผ่านมา
Ex 12.5 Space Flight Dynamics Craig A. Kluever A rigid axisymmetric satellite has principal moments of inertia I1 = I2 = 90 kg-m 2 and I3 = 140 kg-m 2 . At time t = 0, the satellite has angular velocity ω0 = 0.126040u1 - 0.072769u2 0.684703u3 rad/s as expressed in 123 bodyframe coordinates. Determine if the following angular velocity vectors at arbitrary time t = t1 represent a feasible solutio...
Ex 12.4 Space Flight Dynamics Craig A. Kluever
มุมมอง 5712 ชั่วโมงที่ผ่านมา
Ex 12.4 Space Flight Dynamics Craig A. Kluever A rigid-body satellite has 123 body-fixed coordinates that correspond to principal axes. At a particular time instant, the satellite has angular velocity ω = 0.1u1 - 0.2u2 0.6u3 rad/s and angular momentum H = 3u1 - 6u2 57u3 kg-m2/s. a) Determine the satellite’s moment of inertia about its spin axis at this instant. b) Determine the satellite’s iner...
Ex 12.1 Space Flight Dynamics Craig A. Kluever
มุมมอง 1312 ชั่วโมงที่ผ่านมา
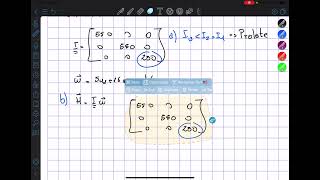
Ex 12.1 Space Flight Dynamics Craig A. Kluever A satellite has the following inertia matrix I = 550 0 0 0 550 0 0 0 280 kg-m 2 and angular velocity ω = 5u2 16u3 rad/s in 123 body coordinates. a) Is the satellite oblate or prolate? Explain your answer. b) Determine the angular momentum vector in 123 body coordinates. c) Determine the rotational kinetic energy.
Ex 12.2 Space Flight Dynamics Craig A. Kluever
มุมมอง 412 ชั่วโมงที่ผ่านมา
Ex 12.2 Space Flight Dynamics Craig A. Kluever A satellite’s principal moments of inertia are I3 = 95 kg-m 2 and I1 = I2 = 60 kg-m 2. The satellite is to be “spun up” from zero rotational kinetic energy to a pure spin of ω3 = 0.7 rad/s about its 3 axis using reaction jets that produce a total torque M3 = 5.5 N-m about the 3 axis. Determine the total thruster time to complete the spin-up maneuver.
Ex 12.3 Space Flight Dynamics Craig A. Kluever
มุมมอง 1012 ชั่วโมงที่ผ่านมา
Ex 12.3 Space Flight Dynamics Craig A. Kluever Show that the time-rate of rotational kinetic energy for an axisymmetric satellite (where I1 = I2 ) subjected to external torques M = M1u1 M2u2 M3u3 is T rot = ω M where ω = ω1u1 ω2u2 ω3u3 and u1, u2, and u3 are unit vectors along the satellite’s 123 body-fixed axes.
Ex 4.2 Space Flight Dynamics Kluever
มุมมอง 3หลายเดือนก่อน
An Earth-observation satellite has perigee and apogee altitudes of 350 and 1,206 km, respectively. Determine the satellite’s flight time from true anomaly θ1 = 270 to θ2 = 90
Ex 4.5 Space Flight Dynamics Kluever
มุมมอง 172 หลายเดือนก่อน
A space probe is departing Earth orbit on a parabolic trajectory. Determine the flight time from perigee (where the altitude is 350 km) to the position on the parabolic path where it crosses geostationary orbit (i.e., the radial distance is 42,164 km)
Ex 3.1 Space Flight Dynamics Kluever
มุมมอง 82 หลายเดือนก่อน
An Earth-orbiting satellite has the following position and velocity vectors in the ECI frame r =[ − 6,796, 4,025 3,490]km, v = [− 3 7817, − 6 0146, 1 1418] km/s Determine the six classical orbital elements.
Ex 2.1 Space Flight Dynamics
มุมมอง 232 หลายเดือนก่อน
An Earth-orbiting satellite has the following position and velocity vectors expressed in polar coordinates: r = 8,250ur km v = 1 2054ur 7 0263uθ km/s Determine the following: a) Angular momentum (magnitude), h b) Specific energy, ξ c) Semimajor axis, a d) Parameter, p e) Eccentricity, e f) Perigee and apogee radii, rp and ra g) Flight-path angle, γ, at this instant h) True anomaly, θ, at this i...
Ex. 2.2 Space Flight Dynamics
มุมมอง 122 หลายเดือนก่อน
Repeat Problem 2.1 for an Earth-orbiting satellite with the following position and velocity vectors expressed in polar coordinates: r = 9,104ur km v =− 0 7004ur 6 1422uθ km/s
Ex 2.7 Space Flight Dynamics Kluever
มุมมอง 62 หลายเดือนก่อน
An Earth-orbiting satellite has semimajor axis a = 9,180 km and eccentricity e = 0.12. Determine the radial position r, velocity v, and flight-path angle γ when the satellite is approaching Earth and 80 from perigee passage.
Ex 2.7 Space Flight Dynamics
มุมมอง 112 หลายเดือนก่อน
At a particular instant in time, a tracking station determines that a space vehicle is at an altitude of 390.4 km with an inertial velocity of 9.7023 km/s and flight-path angle of 1.905 . Is this space vehicle in a closed orbit about the Earth or is it following an open-ended trajectory that will eventually“ escape” Earth? Justify your answer
Ex 2.16 Space Dynamics Kluever
มุมมอง 22 หลายเดือนก่อน
A launch vehicle experiences a malfunction in its guidance system. At burnout of its upper rocket stage, the vehicle is at an altitude of 250 km with an velocity of 7.791 km/s and flight-path angle of 4.5 . Has the vehicle achieved a stable orbit? Explain your answer.
Ex 2.17 Space Flight Dynamics Craig A Kluever
มุมมอง 362 หลายเดือนก่อน
Figure P2.17 shows two satellites in Earth orbits: Satellite A is in a circular orbit with an altitude of 800 km, while Satellite B is in an elliptical orbit with a perigee altitude of 800 km. At the instant shown in Figure P2.17, Satellite B is passing through perigee while Satellite A lags behind Satellite B with an angular separation of 60°. Determine the apogee altitude of the elliptical or...
Classical Mechanics Test Chap 4 John R. Taylor
มุมมอง 263 หลายเดือนก่อน
Classical Mechanics Test Chap 4 John R. Taylor
Streamlines, pathlines and streaklines
มุมมอง 43 หลายเดือนก่อน
Streamlines, pathlines and streaklines
Non dimensional Navier-Stokes equations
มุมมอง 4110 หลายเดือนก่อน
Non dimensional Navier-Stokes equations
Ex. 3.3 Feedback Control of Dynamic Systems
มุมมอง 126ปีที่แล้ว
Ex. 3.3 Feedback Control of Dynamic Systems
Ex. 3.2 Feedback Control of Dynamic Systems
มุมมอง 87ปีที่แล้ว
Ex. 3.2 Feedback Control of Dynamic Systems
Block Diagrams Feedback Control of Dynamic Systems Part 2
มุมมอง 55ปีที่แล้ว
Block Diagrams Feedback Control of Dynamic Systems Part 2
Block Diagrams Feedback Control of Dynamic Systems Part 1
มุมมอง 235ปีที่แล้ว
Block Diagrams Feedback Control of Dynamic Systems Part 1
Final Value Theorem Feedback Control of Dynamic Systems
มุมมอง 33ปีที่แล้ว
Final Value Theorem Feedback Control of Dynamic Systems








Thanks sir ❤
Youre awesome
thank you very much
Nice Work!
10:54 how did you solve that coupled differential equation 😢
Thank you
heeyyy, kolay gelsinn!! 🫠
sanada kolay gelsin!!
@@selin4393 bundan bi sonraki olan example 7.9’a bakabildin mi, line integral’in icinden cikamadim
@@ErenCengiz-xu9wx sinava mayista girdim cok guzel gecti:) sorulari sadece cozmeyi ogren eger zamanda kisitliysan
@@selin4393 hayir daha 3 ayim var, rahatım; çok sevindim senin adına, uk'de mi okuyorsun?
Thanks for the help, for part c is there any chance you switched the values of q and N in the multiplicity equation? You have N=10 but the denomination is 10!(20-1)! instead of 20!(10-1)!. Perhaps I am making a mistake though
Yes that is a mistake
Nice bro keep it up❤
Hello, I am working on this question and I was wondering why side A and side C the work is not zero given constant volume? The equation in the book says W = -p(Deltat V).
Thanks so much!!!
Why is B=1 at the end?
why have we used a linear charge density for the charge of the cylinder?
I guess because of symmetry, you only look at the electric field lines from the smaller to the bigger cylinder in terms of radius s and you get Qenc = λL and ∫E*da = E2πsL = λL/ε0 -> E = λ/(2πsε0) in ŝ-direction with ε0 i mean epsilon with subscript 0 ofcourse
There is no sound in this video
Thank you so much!
At 1:24, shouldn’t R4 be [0,-15,-3]?
I'm afraid you are correct. Sorry for the mistake
Vai così❤️
So what's that determinmant at the end please add little longer explanation please
This was super helpful, thank you!
I still didn’t get what r means and is “t” for?
Although there is same example solved in book but still I don’t understand this question
great video
but in the textbook it says the current goes clockwise
Thank You Sir
Wrong title
Fixed, thank you
Respected sir how did you make the equations for y and z in the last part please tell me
what is (s) please?
What do you mean by (s)?
Thanks for the video, I have a question though, for part (b) should the total multiplicity of the system not be the sum from q= 0 to 20 of the multiplicity function with N constant at 20? I'm just a little confused on total multiplicity vs the multiplicity of a single state.
Hello! I'm not sure I understand the question correctly, but I'll try to explain anyway. We are trying to find the total number of microstates for a system of two solids. One way would be to find all the microstate in each macrostate and add them together. This method is correct, but long. We can do the same by simply imaginingin that instead of having two solids we have one (with the number of oscillators equal to the total number of oscillators in the system) . By doing this we can find all the microstate at once. To re-cap, instead of finding multiplicity (microstate) of every single macrostate and add them together, we can find the total number by assuming that the system is one single solid. Hope this helps, let me know if you have any more questions.
nice keep it up
thank you
Please next chapter's examples
????
I can help you
7.9
maybe im being daft, but why do we have I times (pi s^2)/(pi R^2)?
What step are you referring to?
When we are inside the wire where s<R, Why did we get: I free enc = I * ( pi*s^2 ) divided by (pi*R^2) Thank you.
I could be wrong but: I is the total current in the wire so if you want a tiny, infinitesimal current you divide I by pi*R^2 (the total cross section area). Then you need to multiply that infinitesimal current by the total cross sectional area you're looking at, a.k.a. (I/(pi*R^2))*pi*s^2. Where s=R outside the cylinder and s is just s inside the cylinder. Notice that the whole thing reduces to just the total current, I, outside the cylinder since we care about the entire current when our boundary is greater than R.
Hope that helps even though it's 8 months later.
@@115xXzombieXx115 i got it in time for my eletromag mid terms, in wich i was quite successful! thanks for your help
how do you calculate field B=μ0*M?Could you prove it using Amperes law?
That’s given by the book. I believe I have a video about it too
Thank you
isn't it I=mg/aB?
You’re right, I made an algebra mistake. I’ll make sure to add it to the description
Amazing solution thank you sir
Hi, I'm so happy to find a recent update on this example after hours of desperate search. My problem is that I couldn't really see the boundary condition iv. All the explanations I've seen online seem to be from the original text of the book, i.e. as we go further away from the strip down the x direction, the potential shrinks to zero. However, the potential of the strip is V0(y), which means it is independent of z and thus the strip will have a constant potential value over z direction from z=0 to z=infinity. As far as I can imagine, this V0(y) on the strip can only be made from some infinite charge distribution (for example, an infinite line charge distribution parallel to z-axis). Because of this infinite charge distribution configuration (assumed by me), I find it hard to accept the boundary condition iv. Did I miss something here? Could you please help to better rationalize the boundary condition iv?
The plate with V0 goes from z= negative infinity to z= positive infinity. So it’s independent of z. Condition IV says that it’s dependent on x
Hey dude if you read my comment It might be random but I need your help very urgently Kindly do a reply.
How can I help you?
Hello there! I have a request.. Can you teach us the book? :')
I can try, but that will have to be done during winter, is that okay with you?
By the way, if you have any exercises that you can’t solve I’ll be happy to make a video about them
@@ProjectPatimo I'm taking this course now... By winter I'll be done with the semester. And okay thats nice of you!! Is there a way to contact you better than youtube in case i have a question? Thank you in advance 🙏❤️
I’ll try my best, but I’m taking five courses this semester so my schedule is pretty packed with work as well. I feel like explaining how to do the problem is more important as this stuff is going to be used for other courses and you don’t need to understand the concepts but how to setup the problem. You can comment as much as you want here, if you can private message me I’ll share a contact information