
- 82
- 26 730
Ginger Math
เข้าร่วมเมื่อ 1 ม.ค. 2024
Yes - fun math with a ginger! Mostly all forms of calculus, complex analysis, analytic number theory, and diff eq, with a bit of physics sprinkled on top on Phridays.
Special thanks to Maria for the awesome banner!!
Special thanks to Maria for the awesome banner!!
Interstellar Black Holes (Schwarzschild Metric) | #PhysicsPhriday 11
I'll be rewatching this cinematic masterpiece soon :) #interstellar
Wiki uses a really weird metric signature but it's a good resource as usual:
en.wikipedia.org/wiki/Derivation_of_the_Schwarzschild_solution
And yes, this was recorded on a Phriday and then just posted Saturday morning...
Wiki uses a really weird metric signature but it's a good resource as usual:
en.wikipedia.org/wiki/Derivation_of_the_Schwarzschild_solution
And yes, this was recorded on a Phriday and then just posted Saturday morning...
มุมมอง: 85
วีดีโอ
Free Fallin' into Geodesics (#PhysicsPhriday 10)
มุมมอง 5914 วันที่ผ่านมา
Now I'm freeee, freeee fallin'... but I'm learning to fly... I didn't get that mixed up, did I? There's a chance this video is being posted early on a Saturday morning but I swear it was recorded on Friday :) Helpful Bits: en.wikipedia.org/wiki/Geodesics_in_general_relativity (0:00) Happy Thanksgiving! (0:19) Deriving the Free Fall Eqn (8:50) The Newtonian Limit (16:35) Not Just Free Fall!
A Sigma Proof (Complex Analysis)
มุมมอง 11528 วันที่ผ่านมา
Next video: Ginger Apologizes for Inappropriate use of "Sigma" (0:00) Intro and f Assumptions (1:35) Integer Residues (4:15) Contour Integration (7:35) Upper Bound of |cot| (13:12) Yes, f goes to 0 (14:27) We did it!!
Literally. Logs. (MIT Integration Bee)
มุมมอง 185หลายเดือนก่อน
Semifinal #2 Problem 2: math.mit.edu/~yyao1/pdf/2024_semifinal.pdf
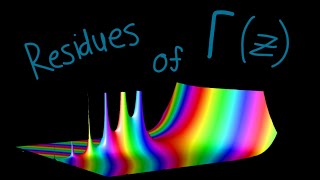
Dew You Know the Residues of the Gamma Function?
มุมมอง 70หลายเดือนก่อน
More complex analysis to come :)
Zeta-ing a Zesty Sum
มุมมอง 152หลายเดือนก่อน
Original Post! math.stackexchange.com/questions/4985650/show-zeta2-1-sum-s-3-infty-1s1-zetas
Complex Analysis-ing a STUPENDOUS @maths_505 Integral
มุมมอง 382หลายเดือนก่อน
Check out @maths_505 original video! th-cam.com/video/9DV0R5W9feA/w-d-xo.htmlsi=3xY4UHaRXx151yKi More complex analysis in the works as well :) (0:00) Introoooo (0:30) Integrals Around the Contour (12:52) Complex Analysis (mini edition) (20:53) RESIDUES
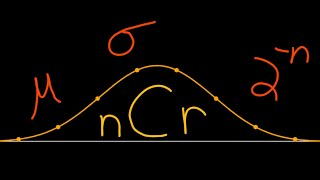
What's the MEANing of This...? (nCr Mean & Stdev)
มุมมอง 622 หลายเดือนก่อน
Project is still going... lots of fun though with the Galton Board :) Here's that identity as well: en.wikipedia.org/wiki/Combination#Number_of_k-combinations
Besting a Berkeley Integral (Complex Analysis-ing)
มุมมอง 2602 หลายเดือนก่อน
Also check out Maths505's take: th-cam.com/video/YJ6j1DXS4AU/w-d-xo.htmlsi=OiXFRpL5jeXQ5DrR
You Spin Me Like a Squircle Baby (#PhysicsPhriday 9)
มุมมอง 812 หลายเดือนก่อน
You spin me right round baby right round like a [squircle] baby right round round round...
e-ATING Up a Sum
มุมมอง 772 หลายเดือนก่อน
Yummmmm... en.wikipedia.org/wiki/Bell_number oeis.org/A000110 (0:00) Intro Short Life Update (0:40) Sum-ing (9:27) Bell Numbers Induction
Ginger Tries His Hand at Environmental Science
มุมมอง 592 หลายเดือนก่อน
Ecosystem Services Project for AP Environmental Science! Another math video on the way :)
Raising the Roof with Ceiling Dion
มุมมอง 7212 หลายเดือนก่อน
My heart will go ooooonnnn... Credit to Noemi for the title :) Quarterfinal #3, Problem 2: math.mit.edu/~yyao1/pdf/2022_quarterfinal.pdf (0:00) Video Bit (13:30) Blooper
The Beta-Zeta Combo
มุมมอง 2953 หลายเดือนก่อน
This has been one of my favorite videos yet!! :) Lower Incomplete Gamma Function Bit: th-cam.com/video/NO3EaJBiPaw/w-d-xo.html Dirichlet Beta function: en.wikipedia.org/wiki/Dirichlet_beta_function Yes, I swear this works: www.desmos.com/calculator/y605ozegsq (0:00) Intro (0:22) Expansion (4:24) Lower Incomplete Gamma Function (6:37) Unit Circle Bits (8:05) Sum More Summing (12:34) Sum #1 (Zeta...
Half a Gamma?! - The Incomplete Gamma Function
มุมมอง 1803 หลายเดือนก่อน
Half a Gamma?! - The Incomplete Gamma Function
A Hot Potato Weighs more than a Cold One?! #PhysicsPhriday 8
มุมมอง 513 หลายเดือนก่อน
A Hot Potato Weighs more than a Cold One?! #PhysicsPhriday 8
Looting a Log Integral with Complex Analysis
มุมมอง 1503 หลายเดือนก่อน
Looting a Log Integral with Complex Analysis
Speedrunning Complex Analysis-ing a NUTS @maths_505 Integral
มุมมอง 1394 หลายเดือนก่อน
Speedrunning Complex Analysis-ing a NUTS @maths_505 Integral
The Kth Dimensional Squircle - Squircles FINALE!
มุมมอง 1114 หลายเดือนก่อน
The Kth Dimensional Squircle - Squircles FINALE!
Great EXPectations - Laplace Transforms
มุมมอง 1.3K4 หลายเดือนก่อน
Great EXPectations - Laplace Transforms
Greek Letter Tier List - 250 SUB SPECIAL
มุมมอง 645 หลายเดือนก่อน
Greek Letter Tier List - 250 SUB SPECIAL
Complex Analysis-ing a CRAZY Integral
มุมมอง 4215 หลายเดือนก่อน
Complex Analysis-ing a CRAZY Integral







how did you learn how to integrate these kinds of functions like the ones in the MIT integration bee? I would love to learn this stuff!! Do you have a discord where we can talk?
yknow i really wish ginger maths friend was in this
If only you had a method of contact outside of the comments section...
40 minutes of pure ginger math! we are so lucky
Black holes were popularized by television and movies beginning in the 1960's. Einstein repeatedly said that they cannot exist. He wrote in 1939 - "The essential result of this investigation is a clear understanding as to why the Schwarzchild singularities (Schwarzchild was the first to raise the issue of General Relativity predicting singularities) do not exist in physical reality. Although the theory given here treats only clusters (star) whose particles move along circular paths it does seem to be subject to reasonable doubt that more general cases will have analogous results. And this is due to the fact that otherwise the constituting particles would reach the velocity of light". He was referring to dilation. It's the phenomenon our high school teachers were talking about when they said "mass becomes infinite at the speed of light". This doesn't mean mass increases, it means mass becomes spread throughout spacetime relative to an outside observer. Time dilation is just one aspect of dilation. Even mass that exists at 75% light speed is partially dilated. It occurs wherever there is an astronomical quantity of mass. This includes the centers of very high mass stars and the overwhelming majority of galaxy centers. The mass at the center of our own galaxy is dilated. This means that there is no valid XYZ coordinate we can attribute to it, you can't point your finger at something that is smeared through spacetime. In other words that mass is all around us. Sound familiar? This is the explanation for dark matter/galaxy rotation curves. The "missing mass" is dilated mass. Dilation does not occur in galaxies with low mass centers because they do not have enough mass to achieve relativistic velocities. It has been confirmed in 6 ultra diffuse galaxies including NGC 1052-DF2 and DF4 to have no dark matter. In other words they have normal rotation rates.
bruh
If you wanted to write me a script for the next Physics Phriday I wouldn't be opposed lol. That's actually really neat though - thanks for all the extra info!
Thanks, I think the concept of singularities is preventing clarity in physics. Relativity does not predict them when you factor in dilation. Nobody believed in them when Einstein was alive including Plank, Bohr, Schrodinger, Dirac, Heisenberg, Pauli, etc. There is no Schwarzchild radius according to Schwarzchild. He was publicly corrected and knew he was wrong. What we see in modern astronomy has been known since 1925. This is when the existence of galaxies was confirmed. It was clear that there should be an astronomical quantity of light emanating from our own galactic center. The modern explanation is because gravitational forces are so strong there that not even light can escape, even though the mass of the photon is zero. The correct explanation is because the mass there is dilated relative to an Earthbound observer.
did u know g=9.81
I just use 10 :)
i saw it first
Actually I did :)
@GingerMath bro thought of a witty reply 9 days later
I forgot about the comment and then saw it when checking analytics lol
Thank you for this video. If you would like to calculate the x value corresponding to a 95% confidence interval with df > 2, how can you apply the approximate function? It will be exciting if I can watch an example in your new video!
🌲🌳 log
Naturally
freaky sonic video next
ur bald fans (me) were anxiously awaiting this video
One can make life simpler by choosing b as the Feynman parameter. dI/db = 2b \int^{\infty}_{-\infty} dx i/(x^2+a^2)(x^2+b^2) = 2\pi /a 1/(b+a) by contour integration. Then I =( 2\pi/a )ln(b+a) + c. Setting b=0, we get J=\int^{\infty}_{-\infty} dx ln(x^2)/(x^2+a^2) = (2/pi /a )ln a . Thus, c = 0. So, I = ( 2\pi/a )ln(b+a).
zesty
can you explain eulers identity
integrating for funsies?
Always for funsies :) But that would be a great title - Fourier for Funsies... ok yeah that's going to be an upcoming video (and an excuse to do Fourier things (if there needs to be a reason in the first place :) ))
ginger math biology takeover when?
You tell me >:|
this is so neat i love it when people do math neat
I think I’m in the wrong classroom
You ate and left no crumbs
ginger what about cultural ecosystem services :(
I'm sure there will be a Part 2 at some point :)
deforestation bad :( tree good :)
love this man
Imagine taking APES
I can barely hear you
hi! i'm so so confused, do you mind explaining the concept of squircles for a beginner in math to then explain deriving the volume formula. please😭
ceil(x)-x=1-{x} 0<={x}<1, so the geometric series for 1/(1-{x}) converges. The problem, then, is finding the ceiling of the sum, because if {x} is something like .999 the ceiling will be much higher than when it's something smaller like .6
ISABELLA GOT A LOLLIPOP!!!!!!
YES SHE DID! I should include bloopers like that more often
I understand every bit of this!
AWESOME - wanna share it with some friends then? :D
@@GingerMath Already did😂
I always thought those floors and ceilings were so hard.
Ditto! But if you split them up like this they're (hopefully) manageable
Nice video! Are you not forgetting a (-1)^m in the final solution due to the i^2m?
Yes I am... whoops - thanks for pointing that out lol
Hi 🙂Maybe at 16:41 you should add (-1)^m
4:45 Missed a t multiplying the second log.
wow the mic quality is so good
Looks interesting, but I can't figure out what steps you're skipping when you claim an bounds of zero and two for the integral wrt t.
specific heat of potato is about 3.4 kJ/kg
Here’s to hoping you continue this series
Nice one
Very interesting
WOAH!!! 🤯🤯🤯🤯
I've used f(z) = ln(z + ib) / (z² + a²) , b>0 And then contour integration by using upper side rectangular contour with residue at z = ia , and then equating real parts and we got it.
Integration by parts twice and substitution x = tan(t) leads us to the integral -4\int_{0}^{\frac{\pi}{2}}\ln{(cos{(t)})}dt
I'm curious to know how we can the pole at z=i because it is of infinite order and the power series can't be used as well due to the 1/(z+i) being there...any ideas on how to calculate it...?
The singularity at z=i is no longer a pole in this case, but an essential singularity because the Laurent series doesn’t terminate for some finite negative power.
I=int[-♾️,♾️]((1+x^2)^-(n+1))dx x=tan(y) dx=sec^2(y)dy I=int[-pi/2,pi/2](sec^(-2n)(y))dy I=2•int[0,pi/2](sin^0(y)cos^2n(y))dy beta(u,v)=2•int[0,pi/2](sin^(2u-1)(y)cos^(2v-1)(y))dy I=beta(1/2,n+1/2) I=sqrt(pi)gamma(n+1/2)/gamma(n+1)
y=x^t x=y^(1/t) dx=1/t•y^(1/t-1)•dy I=1/t^2•int[0,1](ln(y)ln(1-y)/y)dy u=ln(y) dv=ln(1-y)/y du=dy/y v=-Li_2(y) I=1/t^2•(-ln(y)Li_2(y)|[0,1]+int[0,1](Li_2(y)/y)dy) I=Li_3(1)/t^2 Li_3(1)=sum[k=1,♾️](1^k/k^3)=zeta(3) I=zeta(3)/t^2
what about the arcs tho?
I didn't use complex analysis but simple integration techniques and I got the result Integral(-½ to +½) Γ(1+x) Γ(1-x) dx = (4/π) β(2) = 4G/π Here β is dirichlet beta function.
But ginger sir , your solution is also really cool.
Please dont say lohopitals)
Choise of contours always seems completely arbitrary to me ://
bro forgot to edit out the first take
Well that's embarrassing... but hey it's fixed now :D