
- 32
- 94 843
Tropical Troop
United States
เข้าร่วมเมื่อ 12 ส.ค. 2016
Hello, thank you for checking out my channel.
=====================================
I plan on uploading weekly or bi-weekly, and streaming a few times each week.
Videos will come out slower as I will spend more time making quality content, and edit slower.
=====================================
Hitting the subscribe button helps, and you can unsubscribe anytime.
=====================================
I plan on uploading weekly or bi-weekly, and streaming a few times each week.
Videos will come out slower as I will spend more time making quality content, and edit slower.
=====================================
Hitting the subscribe button helps, and you can unsubscribe anytime.
Interstate 5 Road Trip Timelapse Seattle to San Francisco
We drove from Seattle to the Bay Area on the Interstate Five back during Thanksgiving of last year (November 2023).
Overall, the trip took around 12 hours, and I logged more than 12 hours of camera usage that day.
Disclaimer: I had never used the timelapse feature before and did not know the phone deleted frames the longer the clip ran for :(
Recorded on iPhone 15 Pro.
#roadtrip #i5 #interstate5 #car #driving #westcoast
Overall, the trip took around 12 hours, and I logged more than 12 hours of camera usage that day.
Disclaimer: I had never used the timelapse feature before and did not know the phone deleted frames the longer the clip ran for :(
Recorded on iPhone 15 Pro.
#roadtrip #i5 #interstate5 #car #driving #westcoast
มุมมอง: 123
วีดีโอ
Tailing and Trailing in Minecraft Hardcore | Episode 1
มุมมอง 86ปีที่แล้ว
Texture Packs: Barebones, Faithful x64 Shaders: Sildurs Vibrant, BSL, Chocapic Music: "DREAMCATCHER" by Onycs inspired by rekrap2 hi Discord Link! discord.gg/uAWNSKNJjv
Doing Something for the Community!
มุมมอง 195ปีที่แล้ว
Subscribe and don't forget to leave a like. It's free and you can watch my channel anytime you want. Share if you like the video and want your friends to join. Discord Link! Join for trouble shooting and more :) : discord.gg/uAWNSKNJjv
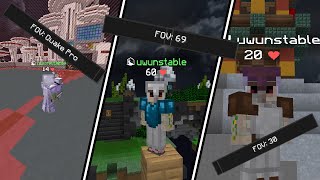
Bedwars but I let random people choose my FOV
มุมมอง 2063 ปีที่แล้ว
Bedwars but I let random people choose my FOV
Bedwars, but I can't see my hotbar or what I'm holding
มุมมอง 1023 ปีที่แล้ว
Bedwars, but I can't see my hotbar or what I'm holding
How to install the new Minecraft Screensaver!
มุมมอง 2323 ปีที่แล้ว
How to install the new Minecraft Screensaver!
How to make a fully flush door with no Button
มุมมอง 814 ปีที่แล้ว
How to make a fully flush door with no Button
How to get an Infinite Lava Source in Minecraft :)
มุมมอง 1.7K4 ปีที่แล้ว
How to get an Infinite Lava Source in Minecraft :)
How To Make A 36 Magic Snake Ball (Updated)
มุมมอง 74K5 ปีที่แล้ว
How To Make A 36 Magic Snake Ball (Updated)
How to find Special quest in Super Power Training Simulator
มุมมอง 3736 ปีที่แล้ว
How to find Special quest in Super Power Training Simulator







what this kid trying do tell? bruh nobody can learn how do a snake ball from watching ur video
please learn the basics of integration first then solve these
Editing as I follow along: for the first one, not much to say you did it perfectly. For the second one also not much to say but to optimize for time you could have just done the power reduction right off the bat and gotten integrals of 1/2 of (1/2)cos(4x) and gotten the same result without the extra U-sub. So far so good! You are improving! EDIT2: I want you to recall something from your algebra days (a^3 + b^3) = (a+b)(a^2 - ab + b^2) and x^3 + 1 = x^3 + 1^3 so x^3 + 1 = (x + 1)(x^2 - x + 1) NOW do the partial fraction decomposing and you end up with 1/3 times integrals of 1/(x + 1) minus 1/3 times integral of (x-2)/(x^2 - x + 1) The first one is just (1/3)ln|x + 1| the second is a slightly more tricky one notice how the derivative of the bottom would be 2x - 1, our goal is to break up the fraction in a way where the derivative of the bottom works to our advantage in a U sub so multiply by 2/2 and push out the 1 half while putting the 2 in the numerator to get (1/6) times integral of (2x - 4)/(x^2 - x + 1) now break apart the fraction into (2x - 1)/(x^2 - x + 1) + (-3)/(x^2 - x + 1) It is now (1/3)ln|x + 1| - (1/6)ln|x^2 - x + 1| + (1/2) times integral of 1/(x^2 - x + 1) for this final one complete the square and you end up with (root(3)/3)tan^-1((2/root(3))(x - (1/2))) So the final answer is as follows (1/3)ln|x + 1| - (1/6)ln|x^2 - x + 1| + (root(3)/3)tan^-1((2x - 1)/root(3)) + C EDIT3: use integration by parts. Set u = x so du = dx and dv = sin^2(x)dx so v = (1/2)(x) - (1/4)sin(2x) so it’s (1/2)x^2 - (1/4)(x)sin(2x) - integral of (1/2)x - (1/4)sin(2x) which comes out to (1/2)x^2 - (1/4)(x)sin(2x) - (1/4)x^2 - (1/8)cos(2x) = (1/4)x^2 - (1/4)xsin(2x) - (1/8)cos(2x) + C EDIT4: nice job on getting 2 in a row right. You did them perfectly. Nice job! as for the cot^5(x) that’s the same as cos^5(x)/sin^5(x) = (cos(x)cos^4(x))/sin^5(x) cos^4(x) = [1 - sin^2(x)]^2 now let u = sin(x) so du = cos(x)dx the integral becomes (u^4 - 2u^2 + 1)/u^5 with respect to u Break apart the fraction and integrate and you get ln|sin(x)| + csc^2(x) - (1/4)csc^4(x) + C
I’m editing this as I follow along. for the first one, multiply by e^-x on top and bottom to force a trig sub. It becomes (e^-x)/(1 + e^-2x) let u = e^-x so du = -e^-xdx the e^-x cancel and you are left with the integrals of -1/1 + u^2 = -tan^-1(u) = -tan^-1(e^-x) + C This can also be written as cot^-1(e^-x) + C (either will satisfy the integral). EDIT: for the second one, whenever there’s an integral of a logarithm involved you should always think integration by parts. Set u = log2(x) so du = 1/xln(2) set dv = 1dx so v = x so it’s xLog2(x) - integrals of 1/ln(2) = xLog2(x) - x/ln(2) + C
I’m following along. This comment will be updated as I watch. So right off the bat I have thoughts. Whenever you have an integral with sec(x) and tan(x) you immediately want to take a sec(x)tan(x) out so you can do a sec(x) u sub with trig identities to turn the tan(x) into a sec(x) so what you should have done was set u = sec(x) so du = sec(x)tan(x)dx now the integral is tan^4(x)sec^2(x) tan^4(x) = (sec^2(x) - 1)^2 So the who’s this is now integral of (u^2 - 1)^2(u^2) = integral of u^6 - 2u^4 + u^2 So the final answer is (1/7)sec^7(x) - (2/5)sec^5(x) + (1/3)sec^3(x) + C EDIT: question 2: nice job! question 3: yikes! but here we go. You need to factor the bottom and do a partial fraction, because it’s a quartic it’s gonna be insanely annoying. I managed to get it to the integral of 1/2(x^2 - root(3)x + 1) + 1/2(x^2 + root(3)x + 1) On each of these you complete the square. (This is where it gets really messy so bear with me). 2 times the integral of 1/(4(x + root(3)/2)) + 1) and 2 times integral of 1/(4(x - root(3)/2) + 1) substituting 2x + root(3) = tan(y) for the first dx = (1/2)sec^2(y) and substituting 2x - root(3) = tan(y) for the second dx = (1/2)sec^2(y) the final answer is tan^-1(2x + root(3)) + tan^-1(2x - root(3)) + C That one was quite tough! I don’t blame you for not getting it (I almost didn’t either). Edit 2: I give up on the 1/(1 + x^5) EDIT3: for the 4(x + e^x)^2 just foil it. so it’s the integral of 4x^2 + 8xe^x + 4e^2x and the integral of that is (4/3)x^3 + 8xe^x - 8e^x + 2e^2x I cleaned it up a bit and got (4/3)x^3 + e^x[e^x + 8x - 8] + C EDIT: csc^3(x)sec(x) = 1/(sin^3(x)cos(x)) and 1 = cos^2(x) + sin^2(x) So you can break it down into two integrals. One of cos(x)/sin^3(x) which is just (-1/2)(1/sin^2(x)) = (-1/2)csc^2(x) the other one is 1/sin(x)cos(x) and this can be again broken down if you substitute cos^2(x) + sin^2(x) for 1 and now it’s the integral of tan(x) + cot(x) which get you ln|sec(x)| + ln|sin(x)| which is ln|tan(x)| by property of logarithms. So the final answer here was (-1/2)csc^2(x) + ln|tan(x)| + C Hope this was helpful. As you can tell I’m not perfect at this because I couldn’t get the 1/(1 + x^5) but I have a decent amount of experience of calc I, II, III and differential equations so Ive seen a fair bit of stuff with integrals. That 1/(x^5 + 1), I will keep trying on it but hopefully one of your other viewers cracks it before me. Have a nice day! I’m definitely subbing.
thanks for the feedback man when i go over all the ones i missed ill definitely pull up ur explanations on the side
oh my god I completely missed this
instantly subbed
this made me love math even more
This is trash
To fast
I really have to put this in the slowest setting in order for it to look like normal speed
THIS is one of the worst tutorials to exist
This is kind of fast
Ya you make it so fast
It’s not even a ball 🥚
You are going to fast
I think it is too fast
Your hands in the way
This is not a tutorial it a “ hey guys look what I made😂
Bro this does not help this is not even a tutorial you’re just speed running it
👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾👎🏾🫥🫥🫥🫥🫥🫥
Why is it so fast i can barely keep up with the pace and its so blurry
If this was a tutorial it sucked
It looks like an egg, not a ball
I thought you were atharva the one with the bird pfp thingy
i am!
this video brightened my day
i know right
Truly a tutorial of all time
ZOOM IN
Can you do it slow
BRO IS SPEED RUNNING HOL UP
bro i can’t see anything
Nice
LoL
Too fast
You cover it and you go so fast you need to work on that
What kind of “how to” video goes this fast
Hay
Nice
horrible tutorial
You have a dog?
It's my cousin's :P Dogs scare me to death
Good job Atharva!!!
I’m not trying to be rude but I hate this tutorial 1:it’s to fast and playback speed isn’t helping 2: it doesn’t make sense 3:their hands are in the way
stop going so fast
I didn't realize that I clicked on a speed run of this.. I was looking for a tutorial lol. Even when you slow the video down its still hard to see and keep up with this.
Slow down
MY MANNN its me gus remember me?
Ye I was thinkin 'bout you yesterday New video in like 5 weeks
Can’t even see the angle and it’s too hard to tell what your turning so what’s the point of this