วีดีโอ

Я бы по другому рисовал! Если не найду - сделаю свое видео!

Спасибо за ваш труд,подскажите пожалуйста откуда вы взяли эти задания?

Try ioqm 2023 questions......2024 was easy but ioqm 2023 level is just 🔥 🔥🔥🔥🔥🔥🔥🔥🔥

👎

15

Uuu

Assalamu alaykum ustoz 👍👍👍 juda zo'r

риба

В Советском Союзе не было ЕГЭ и прочей дури и на учебу оставалось больше времени. Огромный плюс за ролик.

👍

достало весь день ищу видео где норм обьяснят и разложат по полкам формулы сокращеного умножения.так и не нашел все слишком замудряют как и это видео

Thank.

Gracias profesor.

Thanks.

X=tan inverse 1/(2+sq root 3)

Unless the question gives you that restriction that x is an integer number of degrees, then that is a bad final solution. Actually, the phrasing in the red box in the thumbnail puzzled me, I thought there might be some trick allowing for there to be a true maximum instead of just a supremum.

area of ADC=1/2 AD.X.SIN 30 so x=12

Ajoyib 😊

😊 Assalomu alaykum, shayxim salomatmisiz!!?

Too complicated: ABE and BCE are similar, tanx=(2-rt(3))/BE and tanx=BE/(2+rt(3)) thus BE=1 thus tanx=2-rt(3), x = 15

Easier way is to find out DC Which is 6+3×square root of 3 Tanalpha=3/(6+3×squareroot of3) 1/2+squareroot of 3) Alpha =15°

(theorem) in every triangle the rectangle of two sides is equal to the square of the bisector of the angle between them increased by the rectangle of the segments in which the bisector divides the third side referred to the triangle ABC translates into x^2 + BE*AE = BC*AC (1) the right triangles ACD and BCE are similar having an angle equal to half of the angle <BCA and the angles <ADC and <BEC equal as they are complementary of <BCA/2 but <BEC and <DEA opposite the vertex are equal therefore the triangle ADE is isosceles having the base angles DE equal and consequently AD=AE=6 from this similarity the proportion BE:6=x: (x+4) from which BE=6x/(x+4) and the proportion BC:AC=BE:6 from which BC=AC*BE/6= AC *x/(x+4) going back to (1) we can write x^2+6*6x/(x+4) = AC*AC *x/(x+4) (1') (Pythagoras on ACD) AC^2= (x+4)^2 −36 , which replaced in (1') gives x^2(x+4)+36x = x(x+4)^2 −36x … 4x=56 x=14 note ^2 = squared

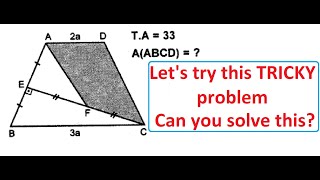
F= meeting point line AE with line BC The triangles ADE and ECF are similar with a similarity ratio of 1 to 3 the sides DE =a and EC=3a being homologous sides in particular EF = 3AE which are also determined by the bisector BE of the angle >ABF in the triangle ABF so the proportion holds AB: (x+CF) = 1:3 , since CF=3AD=18 the previous one turns into 3AB=x+18 and 27=x+18 from which x=9

Solution greatly simplified by using the form: a=b^3-(b-2)^3 when simplified: a=6b^2-12b+8, if b=2022 Then a/6=b^2-2b+1 b^2-2b+1=(b-1)^2 So ((a-2)/6)^1/2=b-1=2021

H^2 = m.n => H =1 e depois Pitágoras.

私はあなたのビデオが大好きです

Καλημέρα σας. Μια άλλη ιδέα. Αφού βρούμε με το θεώρημα διχοτόμου στο τρίγωνο ΑΒC το ΕC, βρίσκουμε με το θεώρημα Stewart το ΑΕ=6. Άρα το τρίγωνο ΑΒΕ είναι ισοσκελές (1). Αν φέρουμε τα ύψη ΑΗ και DZ σχηματίζεται το ορθογώνιο ADZH οπότε ΗΖ=ΑD=x. Από (1)=>ΒΗ=ΗΕ=3/2=1,5. Από την ισότητα των ορθογωνίων τριγώνων (AΒCD ισοσκελές τραπέζιο) ΑΒΗ, DZC έχουμε ZC=BH=1,5. Άρα, BC=BH+HZ+ZC=>7=1,5+x+1,5=>x=4.

This problem can be solved much easier by inspection. ABC must lie on the circumference of a circle. BC is the diameter and the circle radius is 6. It is elementry after that.

Great 👍👍👍👍👍👍👍👍

Another nice example, lots of ways to solve it, I used the property that ABCD is a rhombus, where the diagonal BD is an angle bisector of <ABC If we extend AB and EC, we get the triangle BCK. Let's calculate the BK side: BK/6 = (BK-6)/2 ==> BK=9 Then area of BCK is: S = ½ sin(<ABC) * BC * BK = ½ √3/2 * 6 * 9 = √3 * 27/2 Angle bisector of <ABC divides the side CK and thus the area S in the ratio BC:BK = 6:9 = 2:3 The area of the black triangle is therefore: Sx = 2/5 S = 2/5 * √3 * 27/2 = √3 * 27/5

More interesting problem: Keep Given the same, but make DF : FC =1: 3 instead of 1: 1. What is the area now? There is an easy method to solve this or the original, so long as one knows how F proportionately splits DC. In fact figures are constructible for all ratios, 1 : a with a >= 3/13 . No possible figure if a < 3/13

👍👍

Καλησπέρα σας κ. συνάδελφε. Ασχολήθηκα πριν ημέρες πάλι με την πολύ ωραία αυτή άσκηση και τώρα μόλις βρήκα ευκαιρία να σας στείλω μια 2η λύση. Οι ευθείες ΑΒ, CD τέμνονται στο Ο. Επειδή γωνία ODA=180-(90+α)=90-α και Α=Β=α, η γωνία Ο=180-α-(90-α)=90 δηλ. τα τρίγωνα AOD, BOC είναι ορθογώνια και όμοια. Από τις αναλογίες των πλευρών παίρνουμε: AD/BC=OA/OB=OD/OC (1)=>6/16=OD/(OD+8)=>OD=4,8=>OC=4,8+8=12,8. Από Πυθαγόρειο θεώρημα στο BOC: BC^2=OC^2+OB^2=>OB=9,6. Από (1) => 6/16=ΟΑ/9,6=>ΟΑ=3,6=>x=ΑΒ=9,6-3,6=>x=6.

good luck!

🔥🔥🔥🔥

Alternative solution method: ΔADE and ΔABC are similar by pairs of corresponding sides being proportional, pair AD and AB and pair AE and AC, and the angles between them being equal, in this case, common angle DAE. Side AB is twice as long as side AD, so all dimensions of ΔABC are twice those of ΔADE. Therefore, line segment BC is twice as long as line segment DE. ΔGDE and ΔGCB are next proved to be similar with dimensions of ΔGCB double those of ΔGDE. Thus, both the base and height of ΔGCB are double those of ΔGDE and ΔGCB has 4 times the area, or 24 square units. Construct line segment parallel to BC through point G and label intersection with AB as point F and intersection with AC as point H. ΔAFH and ΔABC are similar, with dimensions ΔAFH being 2/3 those of ΔABC. Height ΔGBC, when BC is considered to be its base, is the difference of heights for ΔAFH and ΔABC, or 1/3 the height of ΔABC, when BC is considered to be its base. Thus, ΔABC has 3 times the height of ΔGBC, with common base BC. Therefore ΔABC has 3 times the area of ΔGBC, or 72 square units.

Totalement faux

amazing videos as usual

Καλησπέρα σας κύριε συνάδελφε. Κατ' αρχάς να εκφράσω την οδύνη μου για αυτό το τρομερό πλήγμα που δέχτηκε η πατρίδα σας αλλά και η Συρία. Δεν υπάρχουν λόγια να εκφράσει κανείς για να συμπαρασταθεί σε αυτές τις δεκάδες χιλιάδες ανθρώπους που επλήγησαν χάνοντας δικούς τους ανθρώπους ή τις εκατοντάδες χιλιάδες, ίσως, ανθρώπους που παραμένουν μέσα στο κρύο άστεγοι. Ας ελπίσουμε για όσο το δυνατόν λιγότερο πόνο στην συνέχεια. Θα μου επιτρέψετε να δώσω μία άλλη λύση καθαρά Γεωμετρική. Φέρνω DE//AB και έστω Ε το σημείο τομής με την BC. Τότε το ABED είναι παραλληλόγραμμο με ΒΕ=ΑD=6=>ΕC=16-6=10, DE=AB=x , γωνία ΑΒΕ=ΑDΕ=α οπότε ΕDC=90+α-α=90 και το τρίγωνο ECD ορθογώνιο. Από θεώρημα Πυθαγόρα: DΕ^2=10^2-8^2=36=>DΕ=6=>AB=DE=6. Ευχαριστώ.

After finding tri.ADE and AE=6 => sin a = 6 / (4+x) = 2/6 (= 1/2 DE / AE). Hence, x=14. Done!

Good luck!

i solve it wo trigonometry. everyone should know that in the right tri with height 1/4 of hyp. tha angle is 15. it has pure geomertrical solution

So beautiful solution !! Your so smart bro )))

Byani tezlashadi

In shaa Alloh oz qoldi

Ajoyib

its 1/3 i think we dont need to the length 6 thank u sir .i am interested in ur videos

ADE=EBC(angle-side-angle). AD=6, BC=10.

(4/2)/6=6/(4+x)

If we know that a square can be "inscribed" in a square, that both have a common center and that a line passing through the center of symmetry divides the figure into equal parts, we can complete the 45-90-45 triangle ∆DEC on the inscribed square and connect AB to the remaining sides of a larger square with area (AB)² = (10+6)² = 256. CD passes through the center of symmetry and thus the area of ABCD is half.