
- 84
- 102 065
GeoSolve
เข้าร่วมเมื่อ 16 เม.ย. 2023
Elegant geometry problems and high quality step by step solutions...
About Me:
I'm a geotechnical / civil engineer who loves geometry since high school years. Solving complex and olympiad level geometry problems is kind of a hobby for me. So, I decided to share solutions of geometry problems which I enjoy the most. I hope you enjoy as well.
What You Can Expect:
I plan to upload a solution every 2 or 3 days. Most of the questions will be from various mathematical olympiads around the world, or some tricky geometry questions I come across here and there. I'll try to add alternative solutions methods, especially trigonometric ones.
How Do I Prepare Videos:
I solve the question first with pen and paper and find all necessary angles and lengths to draw it with a CAD software. So, all geometry questions on this channel are drawn to scale. Then I use MS ppt to create the solution videos.
---
Subscribe to see more mind blowing and relaxing geometry solutions in your feed!
About Me:
I'm a geotechnical / civil engineer who loves geometry since high school years. Solving complex and olympiad level geometry problems is kind of a hobby for me. So, I decided to share solutions of geometry problems which I enjoy the most. I hope you enjoy as well.
What You Can Expect:
I plan to upload a solution every 2 or 3 days. Most of the questions will be from various mathematical olympiads around the world, or some tricky geometry questions I come across here and there. I'll try to add alternative solutions methods, especially trigonometric ones.
How Do I Prepare Videos:
I solve the question first with pen and paper and find all necessary angles and lengths to draw it with a CAD software. So, all geometry questions on this channel are drawn to scale. Then I use MS ppt to create the solution videos.
---
Subscribe to see more mind blowing and relaxing geometry solutions in your feed!
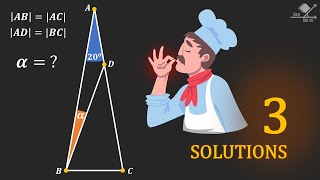
Simple yet DIFFICULT!
In this video, 3 different solution methods for a difficult and challenging geometry question are given.
In triangle ABC, we need to find the missing angle x.
Using the solution of this geometry question, you can learn;
- Internal angles of triangles,
- Congruent triangles,
- Isosceles triangles,
- Equilateral triangles,
- Angle chasing,
- Algebra,
#maths
#mathematics
#geometry
#matholympiadpreparation
#triangle
#equilateraltriangle
#isoscelestriangle
#congruenttriangles
In triangle ABC, we need to find the missing angle x.
Using the solution of this geometry question, you can learn;
- Internal angles of triangles,
- Congruent triangles,
- Isosceles triangles,
- Equilateral triangles,
- Angle chasing,
- Algebra,
#maths
#mathematics
#geometry
#matholympiadpreparation
#triangle
#equilateraltriangle
#isoscelestriangle
#congruenttriangles
มุมมอง: 275
วีดีโอ
This is Beautiful Geometry!
มุมมอง 31814 ชั่วโมงที่ผ่านมา
In this video, 3 different solution methods for a difficult and challenging geometry question are given. In triangle ABC, we need to find the missing angle alpha. Using the solution of this geometry question, you can learn; - Internal angles of triangles, - Congruent triangles, - Isosceles triangles, - Equilateral triangles, - Angle chasing, - Algebra, - Sine Rule, - Some trigonometric identiti...
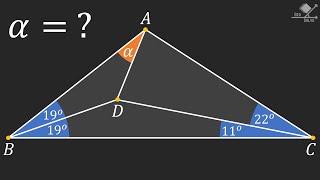
A Nice Geometry Question
มุมมอง 26621 ชั่วโมงที่ผ่านมา
A nice and difficult geometry question. We have a triangle ABC and some angles are given. We need to find the missing angle alpha. Solution of the problem requires the use of; - Internal angles of triangles, - Angle bisectors, - Propertis of Incenters in triangles, - Deltoids, - Some use of algebra. #maths #mathematics #geometry #matholympiadpreparation #triangle #rightangletriangle #isoscelest...
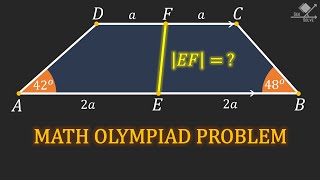
Geometry Olympiad Question from TURKEY!
มุมมอง 323วันที่ผ่านมา
A geometry question from Turkısh Mathematical Olympiads held in 1993. Subscribe: th-cam.com/channels/9XxzHv9RZoqTQPNlzHCnBw.html Instagram: geo.solve #geometry #maths #mathematics #triangle #isoscelestriangle #trapezoid #matholympiadquestion #isosceles #medians #parallelogram
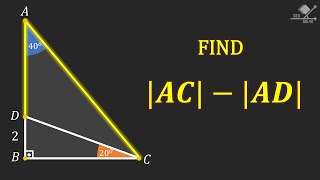
Chaos into Tranquility!
มุมมอง 274วันที่ผ่านมา
A difficult and challenging geometry question. We need to find the difference of two line segments. Solution of the problem requires the use of; - Internal angles of triangles, - Similar triangles, - Isosceles triangles, - Angle chasing, - Algebra #maths #mathematics #geometry #matholympiadpreparation #triangle #rightangletriangle #isoscelestriangle #similartriangles
An Educational Geometry Question!
มุมมอง 36814 วันที่ผ่านมา
An informative and educational geometry question... We need to find the length of the missing side. Solution of the problem requires the use of; - Exterior angle theorem in triangles, - Pythagorean Theorem, - Isosceles triangles, - Angle chasing, - Algebra #maths #mathematics #geometry #matholympiadpreparation #triangle #rightangletriangle #isoscelestriangle #pythagoras_theorem #pythagoreantheorem
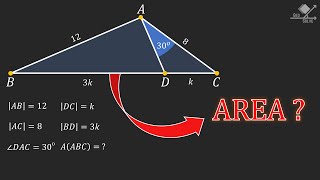
How can you find the AREA?
มุมมอง 32514 วันที่ผ่านมา
A fun and puzzling geometry problem... We need to find the area of the blue shaded triangle. Solution of the problem requires the use of; - Exterior angle theorem in triangles, - 30-60-90 degree triangles, - Angle chasing, - Opposite angles. #maths #mathematics #geometry #matholympiadpreparation #triangle #rightangletriangle #isoscelestriangle #pythagoras_theorem #pythagoreantheorem
Find the AREA of the triangle!
มุมมอง 22014 วันที่ผ่านมา
A triangle geometry question which can be tricky to solve. We are given the lengths of the 2 sides of a triangle, and the remaining side as ratios. Find the area of the triangle. #geometry #matholympiadquestion #matholympiadpreparation #maths #mathematics #triangle #areaoftriangles
Can you Find the missing length? | Geometry Question
มุมมอง 19521 วันที่ผ่านมา
A triangle geometry question which can be tricky to solve. We are given 2 isosceles triangles in a larger triangle. Also, we know the length of 2 line segments. And we need to find the missing length x. Solution of the problem requires the use of; - Properties of isosceles triangles, - Internal angles of triangles, - Cosine law - Angles on a straight line. Subscribe: th-cam.com/channels/9XxzHv9...
Chinese Geometry Olympiad Question
มุมมอง 4.8K7 หลายเดือนก่อน
This is a fairly difficult math olympiad question from China (2004) requiring the use of; - Cyclic quadrilaterals, - Pythagorean theorem, - Isosceles triangles, - Properties of circles, - Angle chasing, - Similar triangles. Subscribe: th-cam.com/channels/9XxzHv9RZoqTQPNlzHCnBw.html Instagram: geo.solve #geometry #maths #mathematics #triangle #matholympiadquestion #trigonometry #c...
Harder than you think!
มุมมอง 4747 หลายเดือนก่อน
A nice triangle geometry question harder than it seems. Solution of the problem requires the use of; - Congruent triangles, - Properties of isosceles triangles - Special triangles. Subscribe: th-cam.com/channels/9XxzHv9RZoqTQPNlzHCnBw.html Instagram: geo.solve Twitter: geometrySolver #geometry #matholympiadquestion #matholympiadpreparation #maths #mathematics #triangl...
Area Challange!
มุมมอง 2427 หลายเดือนก่อน
2 circles are inscribed inside one another, and a chord is tangent to the smaller one. Can you find the area of the region created by this chord? Subscribe: th-cam.com/channels/9XxzHv9RZoqTQPNlzHCnBw.html Instagram: geo.solve Twitter: geometrySolver #geometry #matholympiadquestion #matholympiadpreparation #maths #mathematics #triangle #circlegeometry #circle #circles
The Hard Way or The Easy Way?
มุมมอง 3178 หลายเดือนก่อน
An olympiad level geometry question solved in 2 different ways. Solution of the problem requires the use of; - Similar triangles, - Congruent triangles, - Ptolemy's Theorem, - Pythagorean Theorem, - Cyclic Quadrilateral. Time Stamps For The Solutions: (00:00) - Solution Method - 1 (02:56) - Solution Method - 2 Subscribe: th-cam.com/channels/9XxzHv9RZoqTQPNlzHCnBw.html Instagram: g...
A nice geometry exercise!
มุมมอง 3048 หลายเดือนก่อน
A triangle geometry question which can be tricky to solve. We are given 2 angles of 100 degree and 20 degree. Also, we know that 3 line segments to be congruent. And we need to find the missing angle a. Solution of the problem requires the use of; - Properties of isosceles triangles, - Properties of equilateral triangles, - Exterior angle theorem. Subscribe: th-cam.com/channels/9XxzHv9RZoqTQPNl...
Find the Green Area
มุมมอง 2028 หลายเดือนก่อน
A nice geometry question in which 2 semi-circles and a circle is placed into a square with a side length of 10 units. Area of the green region is asked. Subscribe: th-cam.com/channels/9XxzHv9RZoqTQPNlzHCnBw.html Instagram: geo.solve Twitter: geometrySolver #geometry #matholympiadquestion #matholympiadpreparation #matholympiad #matholympiadexampreparation #maths #mathe...
You can solve this under 20 seconds! Or can you?
มุมมอง 6408 หลายเดือนก่อน
You can solve this under 20 seconds! Or can you?
Can you figure this out? (Trigonometric Approach)
มุมมอง 4488 หลายเดือนก่อน
Can you figure this out? (Trigonometric Approach)
Can you figure this out? (Geometric Approach)
มุมมอง 2.4K8 หลายเดือนก่อน
Can you figure this out? (Geometric Approach)
British Mathematical Olympiad Question!
มุมมอง 4038 หลายเดือนก่อน
British Mathematical Olympiad Question!
Construct & Solve | Geometry Olympiad Question
มุมมอง 2458 หลายเดือนก่อน
Construct & Solve | Geometry Olympiad Question
An Instructive Geometry Question | Find X
มุมมอง 5378 หลายเดือนก่อน
An Instructive Geometry Question | Find X

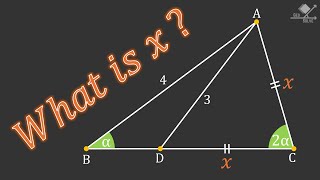


I have a very quick solution
Feel free to share.
X=40
👏
Построим треугольник ∆BDM=∆ACD, где <MBD=30°; <BDM=40°, точка М лежит ниже BC. Тогда ∆MAD=∆BDM по двум сторонам и углу между ними. <MBD=MAD=30°. Четырёхугольник MBAD вписанный. х=<ABD=<AMD=40°
Thanks for sharing your solution. 👍
Nice solutions! I think we can provide a little more details about method 3 - from 2sin10 sin(α+20) = sinα, we get sin(α+20)/sinα = sin30/sin10, so α=10 satisfies it. And sin(α+20)/sinα = (sinα cos20 + cosα sin20)/sinα = cos20 + sin20/tanα, which is decreasing where 0<α<90, so the root α is unique. By the way, I have method 4. Let T is a point on the left side of ABC such that TA = TD = AB. Then △TAD ≡△ABC. As TAD = 80, TAB = 60, so △TAB is equilateral. It means TB = TA = TD, so A, B, D are on a circle which centered T, so ABD = (1/2)ATD = 10
Thanks for improving the trigonometric solution. I thought it would be enough at that point I left at the video. But, that's great. I'll pin this to top for future refrence. Also, your alternative solution method is a creative one. Thanks for adding value. I appreciate it.
Method 3 should be more clear.
You are right. One more step towards the answer would have been nice by me. Now, there is a pinned comment by @SuperPassek that resolved the issue. You can check that out. Thanks for watching.
Классика!
Bu soru gayet basitmiş ayrıca aksanınız türkçeye çok yakın türk müsünüz?
7. sınıf geo lgs sorusu
If you enjoyed the solution, give a thumbs up and comment if you have some different solutions.
Bu bir olimpiyat sorusu değil. Bu lise düzeyinde öğrencilere sorduğumuz bir soru.
If It is too easy for you, you can check some other questions posted earlier. Thanks for watching.
Daha dün çözdüm orijinal geometri de
|DC|=d , |AC|=b , |AD|=a olsun. b kenarını a kenarının yanına ekleyelim ve |DT|= a+b olsun. m(ATC)= 20 derece olur ve bu şekilde üçgen benzerliği yaparız. Şimdi geriye kalan 2. dereceden denklem çözme. c*2 + 4 = d*2 = a*2 + b*2 -2abcos40 denklemini düzenleyelim: -cos40= (a+2)/b -Üçgen benzerliği: 2/c= c/(a+b+2) Gerekenleri yerine yazalım: 2a+2b+8= a*2+b*2 -2a*2 -4a (b-1)*2=(a+3)*2 b-1=a+3 b-a=4 (Sanırım bulunabilecek en bozuk metot bu olabilir😅)
Thanks for the alternative solution. Great effort :)
Construct a perpendicular from D to AC. Call the intersection point E. ∠ACD = 30° ∠ADE = 50° DC = 2/sin20° △CED is 30-60-90 so DE = 1/sin20° AD = DE/sin40° = 1/sin20°·sin40° AC = (AD + 2)/sin50° = ((1/sin20°·sin40°) + 2)/sin50° AC - AD = (((1/sin20°·sin40°) + 2)/sin50°) - (1/sin20°·sin40°) = 4 🤣🤣
😁 That's one way to do it👏👏
Ain't all sides of ADC triangle equal? If then, 2a will be 60 and a will be 30? 60 +30 = 90 and 180-90=90
Triangle ADC is not given to be equilateral. So no. Thanks for the comment.
4
Daha kısa bir yol: C noktasından aşağıya doğru 20 derecelik açı çiz ve AB yi uzat. Kesişim noktası K olsun. m(BKC)=70 |CD|=|CK| |BD| = |BK|=2 cm AKC üçgeni ikizkenardır, çünkü açıları 40, 70, 70 derece |AK|=|AC| |AD|+4 = |AC| 4 = |AC| - |AD|
Great solution👍 Thanks for sharing this.
What kind of software do you use to draw pictures like that
I use autocad to draw questions to scale. Then use ppt to prepare the solutions.
Same as video up to 0:30 in △AED: AD = √3/sin40° Law of sines in △ABD: AD/sin60° = x/sin40° Substitute for AD and rearrange, so x = (√3)sin40°/(sin40°)(sin60°) = √3/sin60° = √3/(√3/2) = (2√3)/√3 = 2
1:56 why DFC is 90 degree?
Angle C is 60 degrees. And it has arms of length k [CF] and 2k [CD]. From this information, we can conclude that triangle DCF is a 30 60 90 degree triangle.
@@GeoSolvethanks!
Sure. Thanks for watching👍
In triangle DFC, use cosine formula to find arm DF, then use cosine formula for angle F
B noktasından açıortayı çizersek, AC kenarını 9k, 7k şeklinde bölecektir. Ayrıca aşağıdaki üçgen ikizkenar olduğu için açıortay uzunluğu da 7k olur. Açıortay uzunluğu formülünden; 9.7 - 9k.7k =(7k)^2 63 - 63.k^2 = 49.k^2 112.k^2 = 63 k=3/4 |AC| = 16.k = 16. 3/4 = 12 Tüm kenarları bulduk. Heron formülünden, u=(9+7+12)/2 =14 A(ABC) = Kök (14.7.2.5) = 14.kök5
Thank you very much for the problem and its solution. An alternative solution consists of drawing a parallel to AD through C and extending BA from B to A to intersect with the parallel to AD through C, lets say at point T. Then, triangles BDA and BCT are similar, thus |BT| = 4*|BA|/3 = 4*12/3 = 16 and thus |AT| = 4. As [angle ACT] = 30° and |AC| = 2*|AT|, the angle CTA must be equal to 90° and, as a consequence, |CT| = 4*sqrt(3). This leads to [ABC] = |AB|*|CT|/2 = 12*4*sqrt(3)/2 = 24*sqrt(3).
Nice alternative solution. Thanks. Similarly, you can also draw a parallel to AC through D. And use similar triangles to show that angle BAD is 90 degrees. Rest is the same.
Что-то долго вас не было в интернете. Мне нравятся ваши задачи!
Glad to be back. Thanks👍
a repeated calculation leads to the result, that the formation must be symmetric: 10 print "geosolve dot dot dash dash":dim x(2,2),y(2,2) 20 l1=9:l2=6:r4=1:r1=2.5: z1=r1^2-r4^2:z2=(l2/l1*r1)^2:z=z1+z2 30 n1=(l2/l1)^2:n2=2*l2/l1: 40 r1max=r4*sqr(1/(1+n1-n2)):print "r1";:if r1=r1max then else 60 50 print "=";r1max:goto 100 60 if r1<r1max then else 80 70 print "<";r1max:goto 100 80 print ">";r1max 90 print "ungueltige eingabe":end 100 goto 170 110 z1=r1^2-r4^2:z2=(l2/l1*r1)^2:z=z1+z2 120 cw=z/2/r1^2/l2*l1:if abs(cw)>1 then return 130 w1=acs(cw):r2=r1*l2/l1:sw3=r2/r4*sin(w1):if abs(sw3)>1 then stop 140 w3=asn(sw3):l4=r4*l2/r2:print "der abstand x=";l4 150 w2=(pi-2*w1-w3)/2:print deg(w2);"%";deg(w3):r5=r2*sqr(2*(1-cos(w2))) 160 z1=r1*sin(2*w1+w2):z2=(r4+r5)*sin(w2):r6=(z1-z2)/sin(w2):fe=r4/r6:fe=1-fe:return 170 gosub 110 180 print "die konstruktion ist ";:if abs(fe)<1E-10 then 200 190 print " a"; 200 print "symmetrisch":gosub 210:goto 360 210 h=r1*sin(w3):lh=r1*cos(w3) 220 x(0,0)=0:y(0,0)=0:x(0,1)=r4:y(0,1)=0:x(0,2)=lh:y(0,2)=h 230 x(1,0)=r4:y(1,0)=0:x(1,1)=r4+r5:y(1,1)=0:x(1,2)=lh:y(1,2)=h 240 x(2,0)=r4+r5:y(2,0)=0:x(2,1)=r4+r5+r6:y(2,1)=0:x(2,2)=lh:y(2,2)=h 250 h=r1*sin(w3):lh=l1*cos(w3):masx=1200/(r4+r5+r6):masy=850/h 260 if masx<masy then mass=masx else mass=masy 270 goto 290 280 xbu=x*mass:ybu=y*mass:return 290 for a=0 to 2:x=x(a,0):y=y(a,0):gosub 280:xba=xbu:yba=ybu:for b=1 to 3 300 ib=b:if ib=3 then ib=0 310 x=x(a,ib):y=y(a,ib):gosub 280:xbn=xbu:ybn=ybu:goto 330 320 line xba,yba,xbn,ybn:xba=xbn:yba=ybn:return 330 gosub 320:next b:next a 340 a$=inkey$(0):if a$="" then 340 else return 350 gosub 110:dg=fe:return 360 sw=sqr(l1^2+l2^2)/100:gosub 350 370 r11=r1:dg1=dg:r1=r1-sw:if abs(cw)>1 then stop 380 r12=r1:gosub 350:if dg1*dg>0 then 370 390 r1=(r11+r12)/2:gosub 350:if dg1*dg>0 then r11=r1 else r12=r1 400 if abs(dg)>1E-10 then 390 410 print "w1=";deg(w1);"°w2=";deg(w2);"°" 420 print "eine taste druecken":gosub 340:cls:gosub 210 der abstand x=5 38.9424413%38.9424413 w1=31.5863381°w2=38.9424413° eine taste druecken
Thanks
hi again! after a lots of calculations i have found out, the formation will only be symmetric if r1=1.8 (look at line 20): 10 print "geosolve dot dot dash dash":dim x(2,2),y(2,2) 20 l1=9:l2=6:r4=1:r1=1.8:z1=r1^2-r4^2:z2=(l2/l1*r1)^2:z=z1+z2 30 n1=(l2/l1)^2:n2=2*l2/l1: 40 r1max=r4*sqr(1/(1+n1-n2)):print "r1";:if r1=r1max then else 60 50 print "=";r1max:goto 100 60 if r1<r1max then else 80 70 print "<";r1max:goto 100 80 print ">";r1max 90 print "ungueltige eingabe":end 100 cw=z/2/r1^2/l2*l1:w1=acs(cw):r2=r1*l2/l1:print "r2=";r2 110 sw3=r2/r4*sin(w1):if abs(sw3)>1 then stop 120 w3=asn(sw3):l4=r4*l2/r2:print "der abstand x=";l4 130 w2=(pi-2*w1-w3)/2:print deg(w2);"%";deg(w3):r5=r2*sqr(2*(1-cos(w2))) 140 z1=r1*sin(2*w1+w2):z2=(r4+r5)*sin(w2):r6=(z1-z2)/sin(w2):fe=r4/r6:fe=1-fe 150 print "die konstruktion ist ";:if abs(fe)<1E-10 then 170 160 print " a"; 170 print "symmetrisch":h=r1*sin(w3):lh=r1*cos(w3) 180 x(0,0)=0:y(0,0)=0:x(0,1)=r4:y(0,1)=0:x(0,2)=lh:y(0,2)=h 190 x(1,0)=r4:y(1,0)=0:x(1,1)=r4+r5:y(1,1)=0:x(1,2)=lh:y(1,2)=h 200 x(2,0)=r4+r5:y(2,0)=0:x(2,1)=r4+r5+r6:y(2,1)=0:x(2,2)=lh:y(2,2)=h 210 h=r1*sin(w3):lh=l1*cos(w3):masx=1200/(r4+r5+r6):masy=850/h 220 if masx<masy then mass=masx else mass=masy 230 goto 250 240 xbu=x*mass:ybu=y*mass:return 250 for a=0 to 2:x=x(a,0):y=y(a,0):gosub 240:xba=xbu:yba=ybu:for b=1 to 3 260 ib=b:if ib=3 then ib=0 270 x=x(a,ib):y=y(a,ib):gosub 240:xbn=xbu:ybn=ybu:goto 290 280 line xba,yba,xbn,ybn:xba=xbn:yba=ybn:return 290 gosub 280:next b:next a geosolve dot dot dash dash r1<3 r2=1.2 der abstand x=5 38.9424413%38.9424413 die konstruktion ist symmetrisch > run in bbc basic sdl and hit ctrl tab to copy from the results window. you may add "@zoom%=1.4*@zoom%" in the first line.
Thanks for sharing.
Best solution 🎉🎉🎉🎉🎉
Oooooo
Yes
15* I figured it out in less than 10 seconds and with all those wacky formulas which is a lot of extra work
Good job.
I have a side question. Everything in the problem is reasonable, yet when I use the fact that the orthocenter divides altitude into two portions with ratio 2:1 from the base side, I get HC = 2/3 * 24 = 16, and HD = 2/3 * 20 =40/3. Also, in right triangle HDC, HC^2 - HD^2 = DC^2 ≠ 15^2. I don't see a miscalculation incidentally...
😅 seq hi
Hey
1:13 you forgot the "+" in previous lines
Another solution: construct an equilateral triangle with BC as base, let the top vertex of the equilateral triangle be E, connect AE and DE. Angle ABD=AED=10, so ADBE is cyclic quadrilateral, so angle BAD=BED=30.
That 2√3 is a big hint!
at least pose the question for context
Thanks for the advice👍
I followed up on the whole solution. Thank you for that neat flow. However, one thing that I didn’t get is how did you identify that DE was a diameter of the circle to deduce the angle EFD is a right angle? I couldn’t find a reason of why to consider it as a diameter?
It is shown on the video thumbnail that DE is the diameter. But, you are right. Maybe I should have mentioned it at the start of the video to clarify. Thanks for the comment 👍
Clear! Thanks for the reply. I didn’t pay attention to the thumbnail of the video. Maybe it would be a good idea to list it with the given if the problem. Thanks again for great problems and solutions!
Thanks for the tip. See you on the next one🙂
if i hadn't done things like this before, it would have taken longer than it did. i assumed the center of the circle is on the line from E to point D. the angle in point L is not exactly equal to 90 degrees: 10 print"geosolve-difficult math problem from china" 20 lbc=25:lbd=20:lbe=7:dim x(11,2),y(11,2):sw=1/(lbc+lbd+lbe) 30 xeu=sw:xb=0:yb=0:xc=lbc:yc=0:n=lbc^2+lbd^2+lbe^2 40 xbu=xb:ybu=yb:xcu=xc:ycu=yc:lu=lbe:xmu=0:goto 70 50 yeu=sqr(lu^2-(xeu-xmu)^2):dgu1=(xbu-xeu)*(xcu-xeu)/n:dgu2=(ybu-yeu)*(ycu-yeu)/n 60 dg=dgu1+dgu2:return 70 gosub 50 80 dg1=dg:xeu1=xeu:xeu=xeu+sw:xeu2=xeu:gosub 50:if dg1*dg>0 then 80 90 xeu=(xeu1+xeu2)/2:gosub 50:if dg1*dg>0 then xeu1=xeu else xeu2=xeu 100 if abs(dg)>1E-10 then 90 110 xe=xeu:ye=yeu:lu=sqr(lbc^2-lbd^2):xmu=lbc:xeu=lbc-sw:xcu=xb:ycu=yb:xbu=xc:ybu=yc 120 gosub 50 130 dg1=dg:xeu1=xeu:xeu=xeu-sw:xeu2=xeu:gosub 50:if dg1*dg>0 then 130 140 xd=xeu:yd=yeu:xg11=xb:yg11=yb:xg12=xe:yg12=ye:rem die koordinaten von punkt a berechnen 150 xg21=xc:yg21=yc:xg22=xd:yg22=yd:gosub 160:goto 190 160 a11=yg12-yg11:a12=xg11-xg12:a131=xg11*(yg12-yg11):a132=yg11*(xg11-xg12) 170 a21=yg22-yg21:a22=xg21-xg22:a231=xg21*(yg22-yg21):a232=yg21*(xg21-xg22) 180 a13=a131+a132:a23=a231+a232: return 190 gosub 200: xa=xl:ya=yl:goto 250 200 ngl1=a12*a21:ngl2=a22*a11 210 ngl=ngl1-ngl2:if ngl=0 then print "keine loesung":end 220 zx1=a23*a12:zx2=a13*a22:zx=zx1-zx2 230 zy1=a13*a21:zy2=a23*a11:zy=zy1-zy2 240 xl=zx/ngl:yl=zy/ngl:return 250 xm=(xd+xe)/2:ym=(yd+ye)/2:r=sqr((xm-xd)^2+(ym-yd)^2):print "r zwischen E-D=";r 260 dxu=xe-xb:dyu=ye-yb:xua=xb:yua=yb:k=100:goto 290 270 dxk=k*dxu:dyk=k*dyu:xs=xua+dxk:ys=yua+dyk:dgu1=(xs-xm)^2/n:dgu2=(ys-ym)^2/n 280 dgu3=r*r/n:dg=dgu1+dgu2-dgu3:return 290 gosub 270 300 k1=k:dg1=dg:k=k-sw:k2=k:gosub 270:if dg1*dg>0 then 300 310 k=(k1+k2)/2:gosub 270:if dg1*dg>0 then k1=k else k2=k 320 xf=xs:yf=ys:dxu=xd-xc:dyu=yd-yc:xua=xc:yua=yc:k=100:gosub 270 330 dg1=dg:k1=k:k=k-sw:k2=k:gosub 270:if dg1*dg>0 then 330 340 k=(k1+k2)/2:gosub 270:if dg1*dg>0 then k1=k else k2=k 350 if abs(dg)>1E-10 then 340 360 xg=xs:yg=ys:rem die koordinaten von schnittpunkt ec und bd berechnen 370 xg11=xe:yg11=ye:xg12=xc:yg12=yc:xg21=xb:yg21=yb:xg22=xd:yg22=yd:gosub 160:gosub 200 380 xh=xl:yh=yl:xg11=xa:yg11=ya:xg12=xh:yg12=yh:xg21=0:yg21=0:xg22=lbc:yg22=0 390 gosub 160:gosub 200:xfu=xl:yfu=yl:print "der fusspunkt von a nach bc=";xfu 400 xg11=xf:yg11=yf:xg12=xg:yg12=yg:xg21=xa:yg21=ya:xg22=xfu:yg22=yfu:gosub 160:gosub 200 410 xk=xl:yk=yl:lak=sqr((xa-xk)^2+(ya-yk)^2):print "der abstand a-k"; lak 420 xg11=xf:yg11=yf:xg12=xg:yg12=yg:xg21=xa:yg21=ya:xg22=xk:yg22=yk:gosub 160:gosub 200 430 xi=xl:yi=yl 440 xg11=xe:yg11=ye:xg12=xd:yg12=yd:xg21=xa:yg21=ya:xg22=xk:yg22=yk:gosub 160:gosub 200 450 xj=xl:yj=yl 460 x(0,0)=0:y(0,0)=0:x(0,1)=xfu:y(0,1)=yfu:x(0,2)=xh:y(0,2)=yh 470 x(1,0)=0:y(1,0)=0:x(1,1)=xh :y(1,1)=yh :x(1,2)=xe:y(1,2)=ye 480 x(2,0)=xe:y(2,0)=ye:x(2,1)=xh :y(2,1)=yh :x(2,2)=xi:y(2,2)=yi 490 x(3,0)=xe:y(3,0)=ye:x(3,1)=xj :y(3,1)=yj :x(3,2)=xk:y(3,2)=yk 500 x(4,0)=xe:y(4,0)=ye:x(4,1)=xk :y(4,1)=yk :x(4,2)=xf:y(4,2)=yf 510 x(5,0)=xf:y(5,0)=yf:x(5,1)=xk:y(5,1)=yk:x(5,2)=xa:y(5,2)=ya 520 x(6,0)=xfu:y(6,0)=yfu:x(6,1)=xc:y(6,1)=yc:x(6,2)=xh:y(6,2)=yh 530 x(7,0)=xc:y(7,0)=yc:x(7,1)=xd :y(7,1)=yd :x(7,2)=xh:y(7,2)=yh 540 x(8,0)=xh:y(8,0)=yh:x(8,1)=xd:y(8,1)=yd:x(8,2)=xj:y(8,2)=yj 550 x(9,0)=xj:y(9,0)=yj:x(9,1)=xd:y(9,1)=yd:x(9,2)=xk:y(9,2)=yk 560 x(10,0)=xk:y(10,0)=yk:x(10,1)=xd:y(10,1)=yd:x(10,2)=xg:y(10,2)=yg 570 x(11,0)=xk:y(11,0)=yk:x(11,1)=xg:y(11,1)=yg:x(11,2)=xa:y(11,2)=ya 580 masx=1200/lbc:masy=900/ya:if masx<masy then mass=masx else mass=masy 590 goto 610 600 xbu=x*mass:ybu=y*mass:return 610 for a=0 to 11:gcol a:x=x(a,0):y=y(a,0):gosub 600:xba=xbu:yba=ybu 620 for b=1 to 3:ib=b:if ib=3 then ib=0 630 x=x(a,ib):y=y(a,ib):gosub 600:xbn=xbu:ybn=ybu:goto 650 640 line xba,yba,xbn,ybn:xba=xbn:yba=ybn:return 650 gosub 640:next b:next a:gcol 10:x=xm:y=ym:gosub 600:circle xbu,ybu,r*mass 660 dx1=xb-xc:dy1=yb-yc:dx2=xa-xfu:dy2=ya-yfu:zx=dx1*dx2:zy=dy1*dy2 670 cw=(zx+zy)/sqr(dx1^2+dy1^2)/sqr(dx2^2+dy2^2):wl=deg(acs(cw)) 680 print "tatsaechlich ist der winkel in punkt L=";wl;"°" geosolve-difficult math problem from china r zwischen E-D=7.48845806 der fusspunkt von a nach bc=7.00473622 der abstand a-k8.6155352 tatsaechlich ist der winkel in punkt L=89.948422° > run in bbc basic sdl and hit ctrl tab to copy from the results window
Thanks for your solution.
Spooky action at a distance. GeoSolve, where is the question? .. given? Seems you were in hurry to impress. Bravo !!!
What do you mean where is the question? I didn't get your point.
@@GeoSolve What is ''given'' in this problem?
The video thumbnail is the full question.
@@GeoSolve The thumbnail for a video is _not_ a valid way to present the whole question. C'mon now.
On the future videos, I'll present a detailed given section for the questions.
beautiful
👍
Spooky 😳
👻
i have watched the end of your video and crafted a code that calculates the angle in point c so that the result for alpha will be 32°: 10 print "geosolve-a nice circle puzzle":dim x(1,2),y(1,2) 20 w1=58:w2=50:lbc=1:gosub 30:goto 180 30 lab=lbc*sin(rad(w2))/sin(rad(w1)):lac=lab*sin(rad(180-w1-w2))/sin(rad(w2)) 40 xb=0:yb=0:xc=lac:yc=0:xa=lab*cos(rad(180-w1-w2)):ya=lab*sin(rad(180-w1-w2)) 50 x1=xb:y1=yb:x2=xc:y2=yc:x3=xa:y3=ya 60 a11=2*(x2-x1):a12=2*(y2-y1):a13=x2^2+y2^2-x1^2-y1^2 70 a21=2*(x3-x1):a22=2*(y3-y1):a23=x3^2+y3^2-x1^2-y1^2:gosub 80:goto 130 80 ngl1=a12*a21:ngl2=a22*a11 90 ngl=ngl1-ngl2:if ngl=0 then print "keine loesung":end 100 zx1=a23*a12:zx2=a13*a22:zx=zx1-zx2 110 zy1=a13*a21:zy2=a23*a11:zy=zy1-zy2 120 xl=zx/ngl:yl=zy/ngl:return 130 r=sqr((x1-xl)^2+(y1-yl)^2):rem print r: 140 xm=xl:ym=yl 150 dx1=xl-xb:dy1=yl-yb:dx2=xc-xb:dy2=yc-yb:zx=dx1*dx2:zy=dy1*dy2 160 cw=(zx+zy)/sqr(dx1^2+dy1^2)/sqr(dx2^2+dy2^2):if abs(cw)>1 then stop 170 wal=deg(acs(cw)):return 180 print "der gesuchte winkel=";wal,"°":gosub 250:cls:sw=1:w2=sw:goto 200 190 gosub 30:dg=(wal-32)/180:return 200 gosub 190 210 dg1=dg:w21=w2:w2=w2+sw:w22=w2:gosub 190:if dg1*dg>0 then 210 220 w2=(w21+w22)/2:gosub 190:if dg1*dg>0 then w21=w2 else w22=w2 230 if abs(dg)>1E-10 then 220 240 print "fuer die loesung (32°) muss der winkel w2=";w2;"° sein":gosub 250:end 250 xg11=xb:yg11=yb:xg12=xl:yg12=yl:xg21=xc:yg21=yc:xg22=xa:yg22=ya 260 a11=yg12-yg11:a12=xg11-xg12:a131=xg11*(yg12-yg11):a132=yg11*(xg11-xg12) 270 a21=yg22-yg21:a22=xg21-xg22:a231=xg21*(yg22-yg21):a232=yg21*(xg21-xg22) 280 a13=a131+a132:a23=a231+a232:gosub 80:xe=xl:ye=yl 290 x(0,0)=0:y(0,0)=0:x(0,1)=xc:y(0,1)=yc:x(0,2)=xe:y(0,2)=ye 300 x(1,0)=0:y(1,0)=0:x(1,1)=xe:y(1,1)=ye:x(0,2)=xa:y(0,2)=ya 310 masx=1200/lbc:masy=900/ya:if masx<masy then mass=masx else mass=masy 320 goto 340 330 xbu=x*mass:ybu=y*mass:return 340 for a=0 to 1:gcol 8+a:x=x(a,0):y=y(a,0):gosub 330:xba=xbu:yba=ybu 350 for b=1 to 3:ib=b:if ib=3 then ib=0 360 x=x(a,ib):y=y(a,ib):gosub 330:xbn=xbu:ybn=ybu:goto 380 370 line xba,yba,xbn,ybn:xba=xbn:yba=ybn:return 380 gosub 370:next b:next a:gcol 10:x=xm:y=ym:gosub 330:circle xbu,ybu,r*mass 390 print "eine taste druecken" 400 a$=inkey$(0):if a$="" then 400 410 return geosolve-a nice circle puzzle der gesuchte winkel=27.5644784° eine taste druecken fuer die loesung (32°) muss der winkel w2=64° sein eine taste druecken > run in bbc basic sdl and hit ctrl tab to copy from the results window
Thanks.
it's a repeated calculation with 2 equations with 2 unknown numbers: 10 print "geosolve-beginner friendly solution of a difficult geometry question" 20 lab=1:sw=.1:dim x(3,2),y(3,2):l2=sw:xa=lab/2:ya=lab/2*sqr(3) 30 xc=lab:yc=0:yd=0:xg11=0:yg11=0:xg12=lab/2:yg12=ya:yg21=0:goto 160:rem ein gleichseitiges dreieck 40 dxe=(xc-xa)*l2/lab:xe=xa+dxe:dye=(yc-ya)*l2/lab:ye=ya+dye:rem mit drumherum 50 xg21=lab+l2:xg22=xe:yg22=ye:xd=xg21 60 a11=yg12-yg11:a12=xg11-xg12:a131=xg11*(yg12-yg11):a132=yg11*(xg11-xg12) 70 a21=yg22-yg21:a22=xg21-xg22:a231=xg21*(yg22-yg21):a232=yg21*(xg21-xg22) 80 a13=a131+a132:a23=a231+a232 90 ngl1=a12*a21:ngl2=a22*a11 100 ngl=ngl1-ngl2:if ngl=0 then print "keine loesung":end 110 zx1=a23*a12:zx2=a13*a22:zx=zx1-zx2 120 zy1=a13*a21:zy2=a23*a11:zy=zy1-zy2 130 xl=zx/ngl:yl=zy/ngl:rem print "x=";xl;"y=";yl 140 dgu1=(xl^2+yl^2)/lab^2:dgu2=((xe-xd)^2+(ye-yd)^2)/lab^2:dg=dgu1-dgu2 150 return 160 gosub 40 170 dg1=dg:l21=l2:l2=l2+sw:if l2>10*lab then stop 180 l22=l2:gosub 40:if dg1*dg>0 then 170 190 l2=(l21+l22)/2:gosub 40:if dg1*dg>0 then l21=l2 else l22=l2 200 if abs(dg)>1E-10 then 190 210 sw=yl/sqr((xl-xd)^2+(yl-yd)^2):wa=deg(asn(sw)):print "der winkel in d=";wa 220 masx=1200/xd:masy=900/ya:if masx>masy then mass=masx else mass=masy 230 goto 250 240 xbu=x*mass:ybu=y*mass:return 250 x(0,0)=0:y(0,0)=0:x(0,1)=xc:y(0,1)=yc:x(0,2)=xl:y(0,2)=yl 260 x(1,0)=lab:y(1,0)=0:x(1,1)=xe:y(1,1)=ye:x(1,2)=xl:y(1,2)=yl 270 x(2,0)=xe:y(2,0)=ye:x(2,1)=xl:y(2,1)=yl:x(2,2)=xa:y(2,2)=ya 280 x(3,0)=lab:y(3,0)=0:x(3,1)=xd:y(3,1)=yd:x(3,2)=xe:y(3,2)=ye 290 for a=0 to 3:gcol8+a:x=x(a,0):y=y(a,0):gosub 240:xba=xbu:yba=ybu:for b=1 to 3 300 ib=b:if ib=3 then ib=0 310 x=x(a,ib):y=y(a,ib):gosub 240:xbn=xbu:ybn=ybu:goto 330 320 line xba,yba,xbn,ybn:xba=xbn:yba=ybn:return 330 gosub 320:next b:next a:gcol8:r=ya*sqr((1-1/3)^2):x=xa:y=ya/3:gosub 240:circle xbu,ybu,r*mass 340 geosolve-beginner friendly solution of a difficult geometry question der winkel in d=40 > run in bbc basic sdl and hit ctrl tab to copy from the results window
Thanks for sharing your solution.
I think we could solve it using only pythagorean theorem and thalès theorem by constructing the intersection of (AB) and (EC)
There are many solutions for this, yes I think you can. Thanks for the comment.
either do 2 equations with 2 unknown numbers or calculate the 3rd angle in triangle bcd and apply the sinus formula: 10 print "geosolve-harder than you think":dim x(1,2),y(1,2):w1=40:w2=10 20 l1=2*sqr(3):h1=l1/2*tan(rad(w1+w2)):l3=sqr(h1^2+l1^2/4) 30 dx=l1*sin(rad(w2))/sin(rad(180-2*w2-w1)):lx=l3-dx 40 print "x=";lx:x(0,0)=0:y(0,0)=0:x(0,1)=l1:y(0,1)=0:x(0,2)=(l3-lx)*cos(rad(w1+w2)) 50 x(0,2)=x(0,1)-x(0,2):y(0,2)=(l3-lx)*sin(rad(w1+w2)):x(1,0)=0:y(1,0)=0:x(1,1)=x(0,2) 55 y(1,1)=y(0,2):x(1,2)=l1/2:y(1,2)=h1:masx=1200/l1:masy=900/h1 70 if masx<masy then mass=masx else mass=masy 80 goto 100 90 xbu=x*mass:ybu=y*mass:return 100 for a=0 to 1:gcol 7+a:x=x(a,0):y=y(a,0):gosub 90:xba=xbu:yba=ybu 110 for b=1 to 3:ib=b:if ib=3 then ib=0 120 x=x(a,ib):y=y(a,ib):gosub 90:xbn=xbu:ybn=ybu:goto 140 130 line xba,yba,xbn,ybn:xba=xbn:yba=ybn:return 140 gosub 130:next b:next a geosolve-harder than you think x=2 > run in bbc basic sdl and hit ctrl tab to copy from the results window. as a schoolboy, i did calculations like that with my pocket calculator as follows: read the result, write it on paper, input it in next equation, write next result on paper...
Thanks for sharing your solution.
there is 2 times a repeated calculation to avoid 2nd degree equations: 10 print "geosolve-area challange!":dim x(2),y(2):nu=29 20 r1=3:xm1=r1:ym1=0:r2=2:xm2=2*r1-r2:ym2=0:sw=r2/(r1+r2):xa=0:ya=0 30 n=r1^2+r2^2:xd=xm2-r2:goto 60 40 yd=ym2+sqr(r2^2-(xd-xm2)^2):dgu1=(xa-xd)*(xm2-xd)/n:dgu2=(ya-yd)*(ym2-yd)/n 50 dg=dgu1+dgu2:return 60 gosub 40 70 dg1=dg:xd1=xd:xd=xd+sw:xd2=xd:gosub 40:if dg1*dg>0 then 70 80 xd=(xd1+xd2)/2:gosub 40:if dg1*dg>0 then xd1=xd else xd2=xd 90 if abs(dg)>1E-10 then 80:rem die schnittpunkte berechnen 100 xc=sw:goto 130 110 dyc=(yd-ya)/(xd-xa)*(xc-xa):yc=ya+dyc:dgu1=(xc-xm1)^2/n:dgu2=(yc-ym1)^2/n 120 dgu3=r1^2/n:dg=dgu1+dgu2-dgu3:return 130 gosub 110 140 dg1=dg:xc1=xc:xc=xc+sw:xc2=xc:gosub 110:if dg1*dg>0 then 140 150 xc=(xc1+xc2)/2:gosub 110:if dg1*dg>0 then xc1=xc else xc2=xc 160 if abs(dg)>1E-10 then 150 170 x(0)=0:y(0)=0:x(1)=xm2:y(1)=ym2:x(2)=xc:y(2)=yc:masx=1200/2/r1:masy=900/r1 180 if masx<masy then mass=masx else mass=masy 190 goto 210 200 xbu=x*mass:ybu=y*mass:return 210 x=x(0):y=y(0):gosub 200:xba=xbu:yba=ybu:for a=1 to 3:ia=a:if ia=3 then ia=0 220 x=x(ia):y=y(ia):gosub 200:xbn=xbu:ybn=ybu:goto 240 230 line xba,yba,xbn,ybn:xba=xbn:yba=ybn:return 240 gosub 230:next a:ar=0:gcol5:xul=0:xur=0:yu=0:dx=(xc-xa)/(yc-ya):for a=1 to nu 250 yo=a/nu*r1:xol=xm1-sqr(r1^2-yo^2):if yo<yc then else 270 260 xor=dx*(yo-ya):goto 280 270 xor=xm1+sqr(r1^2-yo^2) 280 da=(xor-xol+xur-xul)/2*r1/nu:ar=ar+da 290 y=yu:x=xul:gosub 200:xb1=xbu:yb1=ybu:x=xur:gosub 200:yb2=ybu:xb2=xbu 300 y=yo:x=xor:gosub 200:xb3=xbu:yb3=ybu:x=xol:gosub 200:xb4=xbu:yb4=ybu:goto 320 310 line xb1,yb1,xb2,yb2:line xb2,yb2,xb3,yb3:line xb3,yb3,xb4,yb4:line xb4,yb4,xb1,yb1:return 320 gosub 310:xur=xor:xul=xol:yu=yo:next a:xl=0:yul=0:yol=0:dy=(yc-ya)/(xc-xa) 330 for a=1 to nu:xr=a/nu*xc:yor=sqr(r1^2-(xr-xm1)^2)+ym2: yur=dy*(xr-xa) 340 x=xl:y=yul:gosub 200:xb1=xbu:yb1=ybu:x=xr:y=yur:gosub 200:xb2=xbu:yb2=ybu 350 y=yor:gosub 200:xb3=xbu:yb3=ybu:x=xl:y=yol:gosub 200:xb4=xbu:yb4=ybu:gosub 310 360 xl=xr:yol=yor:yul=yur:next a:print "die flaeche=";ar:gcol8:x=xm2:y=ym2:gosub 200 370 circle xbu,ybu,r2*mass:x=xm1:y=ym1:gosub 200:circle xbu,ybu,r1*mass 380 geosolve-area challange! die flaeche=5.49345549 > run in bbc basic sdl and hit ctrl tab to copy from the results window
Thanks for sharing your solution.
Thanks for the video, it also helps improve geometry terminology. In this aspect, It is useful for turkish math teachers. 👍
Glad you found the video useful 👍 Thanks for the comment🙏
ich würde mit einem thales kreis anfangen, um die schnittpunkte zu berechnen
I'll start learning German👍
Angle AGC is 120, so it subtends 1/3 of the disc. Trangle ACG is easy. N[3^2*Pi/3 - 3/2* Sqrt[3]*3/2] =~ 5.52766. Avoids trig.
Nice catch. Thanks for the comment👍
Yes but why do you need the area? Is it something to do with planting seeds?
It is for a 1.65MW solar power plant.
Helllo. I am the guy who sent a problem that I couldn't solve about 2 week sago. Have you got some idea?
Hi, I didn't have the time for that.
it all ends up with interpolation in a squared 2nd degree equation: 10 print "geosolve-a nice geometry exercise":dim x(2,2),y(2,2) 20 l1=1:w1=100:w2=20:xa=0:ya=l1*sin(rad(w1)):xb=l1*abs(cos(rad(w1))):yb=0 30 lbc=sin(rad(180-w1-w2))/sin(rad(w2))*l1:xc=xb+lbc:yc=0 40 lac=l1*sin(rad(w1))/sin(rad(w2)):dx=(xc-xa)*l1/lac:xe=xa+dx 50 dy=(yc-ya)*l1/lac:ye=ya+dy:disx=l1^2-ye^2:if disx<0 then stop 60 xd=xe+sqr(disx):yd=0:fe=sqr((xe-xd)^2+(ye-yd)^2)/l1:fe=(1-fe)*100 70 print "der fehler=";fe;"%":lad=sqr((xa-xd)^2+(ya-yd)^2):lbd=sqr((xb-xd)^2+(yb-yd)^2) 80 cw=(l1^2+lad^2-lbd^2)/2/l1/lad:wal=deg(acs(cw)):print "der winkel bad=";wal 90 masx=1200/xc:masy=900/ya:if masx<masy then mass=masx else mass=masy 100 goto 120 110 xbu=x*mass:ybu=y*mass:return 120 x(0,0)=xb:y(0,0)=yb:x(0,1)=xd:y(0,1)=yd:x(0,2)=xa:y(0,2)=ya 130 x(1,0)=xd:y(1,0)=yd:x(1,1)=xc:y(1,1)=yc:x(1,2)=xe:y(1,2)=ye 140 x(2,0)=xa:y(2,0)=ya:x(2,1)=xd:y(2,1)=yd:x(2,2)=xe:y(2,2)=ye 150 for a=0 to 2:gcola:x=x(a,0):y=y(a,0):gosub 110:xba=xbu:yba=ybu:for b=1 to 3 160 ib=b:if ib=3 then ib=0 170 x=x(a,ib):y=y(a,ib):gosub 110:xbn=xbu:ybn=ybu:goto 190 180 line xba,yba,xbn,ybn:xba=xbn:yba=ybn:return 190 gosub 180:next b:next a geosolve-a nice geometry exercise der fehler=0% der winkel bad=50 > the angle could be calculated from the coordinates or the cosinus triangle formula run in bbc basic sdl and hit ctrl tab to copy from the results window
Thanks for sharing.
In the first solution, when you have the isosceles triangle inside the circle, just draw the height through O; the two subtriangles are similar to ABD, so just do the ratios instead of all the trig. Ah, same idea as user-ii5vr3um9r..
Yes, the first solution can be simplified further as you said. Thanks for the comment, and reading others🙂
it works without angle functions, just solve 2 equtions with 2 unknown numbers: 10 print "geosolve-the hard way or the easy way?":dim x(3,2),y(3,2) 20 l1=9:l2=3:l3=sqr(l1^2+l2^2):lh=(l3^2+l1^2-l2^2)/2/l3 30 h=sqr(l1^2-lh^2):lg=sqr((h+l3)^2+lh^2):print lg 40 masx=1200/l3:masy=900/(l3+h):if masx<masy then mass=masx else mass=masy 50 goto 70 60 xbu=x*mass:ybu=y*mass:return 70 x(0,0)=0:y(0,0)=0:x(0,1)=l3:y(0,1)=0:x(0,2)=0:y(0,2)=l3 80 x(1,0)=l3:y(1,0)=0:x(1,1)=l3:y(1,1)=l3:x(1,2)=0:y(1,2)=0 90 x(2,0)=lh:y(2,0)=l3:x(2,1)=l3:y(2,1)=l3:x(2,2)=lh:y(2,2)=h+l3 100 x(3,0)=0:y(3,0)=l3:x(3,1)=lh:y(3,1)=l3:x(3,2)=lh:y(3,2)=y(2,2) 110 for a=0 to 3:x=x(a,0):y=y(a,0):gosub 60:xba=xbu:yba=ybu:for b=1 to 3 120 ib=b:if ib=3 then ib=0 130 x=x(a,ib):y=y(a,ib):gosub 60:xbn=xbu:ybn=ybu:goto 150 140 line xba,yba,xbn,ybn:xba=xbn:yba=ybn:return 150 gosub 140:next b:next a:xba=0:yba=0:x=x(3,2):y=y(3,2):gosub 60:xbn=xbu:ybn=ybu 160 gcol 9:gosub 140 geosolve-the hard way or the easy way? 15 > run in bbc basic sdl and hit ctrl tab to copy from the results window. i had formerly written "h=sqr(l1^2-h^2)" instead which usually results in an error message with the words "not a variable in line 30" but this time, did not.
Thanks for sharing.