
- 142
- 109 118
Robin Zhou
เข้าร่วมเมื่อ 31 มี.ค. 2012
The planned order for textbooks after Griffiths QM is classical mech by Taylor, some sort of intermediate thermo textbook, and then EM by Griffiths.
Donate to me on Venmo @Robin-Zhou-4
Donate to me on Venmo @Robin-Zhou-4
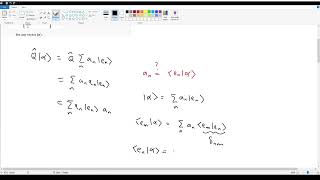
Griffiths QM 3.6.3 - Changing Bases in Dirac Notation
Griffiths QM 3.6.3 - Changing Bases in Dirac Notation
มุมมอง: 214
วีดีโอ
Griffiths QM 3.6.1 - Bases in Hilbert Space
มุมมอง 40710 หลายเดือนก่อน
Griffiths QM 3.6.1 - Bases in Hilbert Space
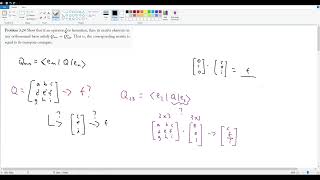
Griffiths QM Problem 3.20
มุมมอง 531ปีที่แล้ว
Support me on Patreon so that I can upload more often. www.patreon.com/RobinZhou Alternatively, donate to me on Venmo @Robin-Zhou-4
Griffiths QM Problem 3.21
มุมมอง 358ปีที่แล้ว
Support me on Patreon so that I can upload more often. www.patreon.com/RobinZhou Alternatively, donate to me on Venmo @Robin-Zhou-4
Griffiths QM Problem 3.22
มุมมอง 355ปีที่แล้ว
Support me on Patreon so that I can upload more often. www.patreon.com/RobinZhou Alternatively, donate to me on Venmo @Robin-Zhou-4
Griffiths QM Problem 3.19
มุมมอง 374ปีที่แล้ว
Support me on Patreon so that I can upload more often. www.patreon.com/RobinZhou Alternatively, donate to me on Venmo @Robin-Zhou-4
Griffiths QM 3.5.3 - Time Energy Uncertainty
มุมมอง 389ปีที่แล้ว
Griffiths QM 3.5.3 - Time Energy Uncertainty
Griffiths QM 3.5.2 - Minimum Uncertainty Wave Packet
มุมมอง 580ปีที่แล้ว
Griffiths QM 3.5.2 - Minimum Uncertainty Wave Packet
Griffiths QM 3.5.1 - Generalized Uncertainty Principle
มุมมอง 439ปีที่แล้ว
Griffiths QM 3.5.1 - Generalized Uncertainty Principle
Griffiths QM 3.4 - Generalized Statistical Interpretation
มุมมอง 785ปีที่แล้ว
Griffiths QM 3.4 - Generalized Statistical Interpretation







thank you
Thank you
amazing
Please upload video for problem 3.37 and 3.38
Your videos have been very helpful. Please, don't stop!
Wow I got the hermitian part but I'm rusty on my diffeq stuff. THe q values were really confuing me. Thanks for a good explanation!
me too
gracias amigo
Thanks!
Thanks so much for the explanation!
Thanks so much!
Thanks so much!!
Nice but .... For integration by parts the differentiation has to be with respect to the integration variable . In this case the differentiation is with respect to t but the integration variable is x that's why we cannot perform integration by parts.
Thanks so much, this was really helpful!
In the book, they got rid of the square root sign on the 1/2. Do you know why?
this was super helpful, thank you!
Thank you, this was a super helpful explanation!
This is Problem 3.18 from 2nd edition
Thanks so much!! This was super helpful.
Thanks! Does the gaussian format only apply to position and momentum, then? I was a bit confused on that last point. The textbook seems a bit more general. It says "Evidently the minimum-uncertainty wave packet is a Gaussian"
Thanks so much! it was so unclear in the book where all these parts were coming from
Since this is just qualitative analysis, how do we know for sure A is between E1 and E2? A could be higher than both E1 and E2?
Thank you so much for this explanation
Thanks so much!!
Hello, Would you please post the codes in Desmos to plot this graph?
Are you still making videos? How much money do you need to get started?
My schedule is currently occupied with other things. I do plan to resume, but it will not be for some time.
@@robinzhou6297 Good luck with the other stuff and happy to hear you have plans to continue in the future :D
For part c, considering behavior as x -> plus infinity, the constant (ik-a/ik+a) has magnitude 1 and thus is just a phase, so the asymptotic wave function is Ae^ikx in both asymptotic limits (i.e., same constant A, as one would expect).
can we say that we know it is the ground state because it has no nodes?
yeesh! Good job!
Thank you for your video.
Hey, if your professor allows you to use the book on homework, I HIGHLY recommend looking at the integrals at the back of the book. I’m only halfway through the class, and plugging my values into these forms has probably saved me hours of time.
ly
I'm an online physics student, and without your videos I honestly don't know how I'd be passing the classes I'm in. Thank you so much for giving such helpful explanations!
Nice video but not including psi star was a little confusing (nvm u fixed it)
This is absolutely excellent explanation!
Thank you dear Sir
thank you for this video. my uni started on chapter three and I had no idea why the equations were the way they were. everything makes sense now. thank you 🙏🙏
OMG!! I tried this for a couple of hours and agree with you 100%
Thank you! At 8:20 et seq., you note that the surface term x(psi)* d/dx (psi) (and a similar 2nd term) go to zero. It seems to me that this is a bit complicated by the presence of x, which goes to infinity while psi goes to zero. In fact, since psi is square integrable, it only has to go to zero faster than x^(-1/2), I think, which would allow x(psi) to still go to infinity as x goes to infinity. As I thought about it, it seemed to me that we are saved by the derivative term, which should go to zero faster than psi -- so psi*(d/dx of psi) goes to zero faster than x^(-1), which saves us. So I agree the entire term goes to zero -- it just is a bit more complicated than for a simple surface term involving only psi.
Wow, very well done! Thank you!
I think b) wants you to choose delta function with positive coefficient and c) delta with negative one.
One could notice that second term while calculating <p^2> is just some constant times <x^2> which was already found
The last argument you gave was only valid in case of infinite square well but not the general case
The hero we needed 🫡
Thank you very much!
at 20:20 and following, shouldn't the sum over n be inside the square, leading to cross-terms for |psi| squared?
Technically yes, but it ultimately doesn't matter in this specific instance because your independent psi_n wavefunctions are part of an orthogonal set. If you actually wrote out an example magnitude squared expression for say, the summation index n going from 1 to 3, you'll see that you'll have a bunch of psi_n^* times psi_m terms, which go to 0 as a result of orthogonality. This is something I probably should have gone over, but I skipped it unconsciously so I will highlight this comment. Thank you.
Thank you for your very helpful videos. Commenting on c. 18:30 et seq., I agree that given a solution psi -- let me call it f for ease of typing -- then f+f* and i(f-f*) are both solutions and are both real but neither is equal to f. The problem asks us to show that a non-real solution can be expressed as a linear combination of real solutions. For example, e^(ikx) = cos(kx) + isin(kx). You have to allow complex coefficients in your linear combination to do this, obviously. So if f=a+bi, then f+f*=2a is real, and -i(f-f*)=2b is real, and f can be written (strangely) as f = 1/2{[f+f*] +i[-i(f-f*)]} -- which is really weird but is in fact both equal to f and a linear combination of real functions. I think your answer is much more helpful physically, since it allows us to switch to a real set of eigenstates and sort of allows eventually to connect with symmetries of the system.
I did not intend to put a line through the equation there. Geez! Sorry
Hello sir ... please upload your lectures regularly if possible. Special thanks from Pakistan ❤❤
Hello sir, sir please make more videos and upload it everyday at least on the second day
Great sir you are really a great man.... Sir please keep it up. We are waiting for more lectures
How can Asin(kx)=0 be a valid solution? If we put x =0, that's still a valid boundary, we'll have that A =0. Couldnt we Just use 0 as an boundary condition to eliminate the solution with sine Just like in the infinite Square well that the book already solves?