
- 100
- 242 591
XYZ + RGB
เข้าร่วมเมื่อ 31 ม.ค. 2017
All things at the intersection of Math (XYZ) and Art (RGB)
วีดีโอ
Mathematics of the Golden Ratio
มุมมอง 221หลายเดือนก่อน
A short lecture on the origins of the Golden Ratio, and an example problem.
Solving a nonhomogeneous system of 1st order D.E.
มุมมอง 1182 หลายเดือนก่อน
Solving a nonhomogeneous system of 1st order D.E.
Advanced Parametric Modeling and Lighting
มุมมอง 4342 หลายเดือนก่อน
This video covers a more advanced example of parametric modeling, as well as some tips for lighting, camera work and other ideas for making your own unique parametric design.
Intro to Parametric Modeling in Blender Geo Nodes
มุมมอง 4972 หลายเดือนก่อน
This video gives an introduction to why parametric modeling is used, and how we can accomplish this using Geometry Nodes in Blender. An example file can be found on canvas under the Exam 3 Notes titled "Parametric.blend" or at the link below. Note that only the first 27 minutes deal with parametric modeling, and the rest of the video is troubleshooting common issues you might be having. If you ...
One Point Perspective Drawing Tutorial (Detailed)
มุมมอง 4223 หลายเดือนก่อน
Once you have learned about the cross ratio, this video will show you how to use the provided excel spreadsheet to create a perspective drawing. For those interested in extending this technique to 2-point and 3-point perspective: th-cam.com/video/taErRVCY1iA/w-d-xo.htmlsi=2l_0nZIwcl2nynZ9
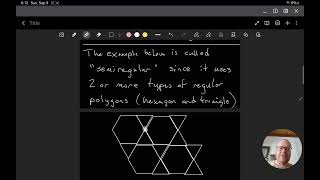
Defining Regular and Semiregular Tiling
มุมมอง 1194 หลายเดือนก่อน
Defining Regular and Semiregular Tiling
Articulate Storyline 360 Example Slide
มุมมอง 557 หลายเดือนก่อน
A sample from the course materials I made for 'Geometry and the Mathematics of Design' at Virginia Tech.
2214 - Answers to Questions from Class
มุมมอง 10710 หลายเดือนก่อน
I go over the removal of the "i" to get a real-valued solution when we have a complex root. I also derive our spring equation from a force diagram.
3D Solids - Volume and Surface Area
มุมมอง 291ปีที่แล้ว
Derivation of the volume of a cone (Optional) www.nagwa.com/en/videos/504142178593/
Finding Measures of Centrality in GeoGebra
มุมมอง 368ปีที่แล้ว
Finding Measures of Centrality in GeoGebra
Conway's Criterion and Nonperiodic Tiling (1 of 2)
มุมมอง 5022 ปีที่แล้ว
Conway's Criterion and Nonperiodic Tiling (1 of 2)
Measures of Centrality, Isometries, and Lines of Reflection in Geogebra
มุมมอง 5142 ปีที่แล้ว
Measures of Centrality, Isometries, and Lines of Reflection in Geogebra
Molotov Cocktail Party - Gut Feeling / Slap Your Mammy
มุมมอง 2142 ปีที่แล้ว
Molotov Cocktail Party - Gut Feeling / Slap Your Mammy
Molotov Cocktail Party - Quarantine Rock
มุมมอง 1402 ปีที่แล้ว
Molotov Cocktail Party - Quarantine Rock








2:29 The value of "E !!" 😆 😗Thx tho, it really help me out
finally I understood why the phi angle is between 0 to 180 degree in the spherical coordinate system. thank you sooooo much !!
Thank you so much, something stuck in my mind for more than 4 hours about this because the teacher at my university just talk about this for 5 minutes then solve 2 problems in 10 minutes so I do not understand enough but you know what not just me but also other students in my class but at the end they are still able to get 9 or even 10 at the exam, but I believe that not many of them know clearly about this, that is so sad about education when someone does not fully understand something and can get a 10 grade but others have to mine and understand deeply which costs a lot of time but in God I trust, the time I spend for math is not worthless. THANK YOU SO MUCH FOR YOUR LECTURE. God blessed you.
@@wonbpoly Once you start to apply this knowledge, you will see the benefit of truly understanding the concepts, and will be helping your peers.
this is brilliant, thank you for your work!!
I have never understood the spherical φ coordinate and how it only goes to π and not 2π until i watched this video, THANKS A LOT <3
For the first time I understood this Finally❤
thank you so much , had a seizure making sense out of this on my textbook , this video cleared alot , realy
i got the visualization today
thank you i've been trying forever to visualize phi
Looks like the settings window was not captured in the recording.
Thank you for letting me know. I'll make a short video when I get home to show this.
Tnanks man
excellent👌👌
*Great explanation Sir. Thanks, lots of love from India*
5:24 why theta limits are from pi to 2pi Could you pls explain
Theta starts at the positive x axis, and moves toward the positive y axis, so it has to travel halfway around and start at pi.
makes learning so interesting
finally a good video regarding this !!! thank you !!!
Very intuitve explanation. Thanks 💯
i have a re-exam and now phi is much more intuitive than the first time!! Thanks very very much for such a good explanation!!!!
a really nice representation thank you
very helpful video! i have a calculus coming up and you have no idea how this saved me hahah thanks a bunch 😊
Good luck on your exam!
nt exactly a music vid, but nice to see someone throwing out some love for talvin singh
true! maybe a "visualizer"?
Thanks! This was extremely helpful :D
So x and y axioms have an angular relationship and the z axioms phi is independent, having half the values because its the same on either side of the axis without concern with position. Hmm interesting stuff.
AMAZING VIDEO THANK YOU SO MUCH
Great explanation sir
what app and OS are you using?
I'm using a samsung tablet running android, the app is the 'Samsung Notes' app that came with it
A good teacher is one who can make complicated topics the most easiest ones. Thank you
Thank you
as in polar coordinate 2d we needed an initial line and pole for frame of reference , i wonder if we need all the three axes here?
Changing the frame of reference from what I described here is a bit more advanced than what I can cover here, but I would assume we need all 3 axes to define a frame of reference.
Thank you so much! this made it so clear
thank you SO MUCH for this video. It got me unstuck. I didn't realize that the vertical angle goes only from 0 to Pi, not to 2Pi, like angles usually would
Great animation.Thanks. You have my subscription. I think greatly of all the pre computer graphics mathematicians who could see it all in their heads.Makes one wonder? In the long run are our brains going to be less or more capable of visualisation?
That's such an interesting question. I feel like we are adding to the number of people that can visualize a topic each time we express it in a new way. There's no shortage of difficult concepts to understand, so I suppose anyone can still exercise the skill as much as they want. I had a colleague suggest that some boys gain an advantage in spatial visualization over girls from jumping off of playground equipment and tracking movements of the ball in sports more often. I have no idea if nature or nurture is the main culprit, but I suspect it's a skill that can be strengthened.
Thanks
This was 3 years ago and no comment, everyone is speechless by such creativity. This is perfect.
GUNA HEMBRAM kist College Reg No -2201214167
BINOD SINGH Kist college Reg No -2201214165
KIST college Se konkon dekh raha hai
This video made me understand why theta is only from 0 to π, thanks!
It's a pleasure to be the first to like and comment on this video! Thank you for the tutorial!
Hi Everyone. I'm realizing I didn't rescale my screen capture, so a lot of this video is covered up. I'll record and upload an updated version tonight.
θ is to reduce the aggregate of three-dimensional space to a surface, Φ is to reduce the aggregate of a surface to a line, which is the intersection of the surface and the cone, and ρ is to reduce a line to a point. The positioning of any point in space can be completed.
This was very concise! Illustrated fantastici! All important key features in order to calculate the transmitted irradience by angular dependent. Using Yours - presented coordinates and the following spherical coordinate system I can specify a given direction for the zenith and azimuth angles thus the transmittance of this system is a function of direction of incident radiation. So valuable information also for the irradience from the sun, sky and for all hemispheric areas given by the independent of changes in the sun or sky radiance. Thank you because performing an integration of the transmitted irradience and calculating the total radiant flux in civil engineering we can see better geometry for example water, glass, polarized elements, i. c. Also we can imply two-dimensional Fourier transform of Cartesian coordinates if we understand better first important step that implys in all disciplines not only engineering approach! 👏👏👏👏
Subscribed❤
this has been incredibly helpful, thank you!
Thank you so much ❤
Great video, keep up the good work!!
I actually appreciate your time, I had finally learnt.
Short and simple but very helpful, thank you so much
Bit Obsolete nowadays but clever editing!!
saved my calc grade thank you🙏
I don't understand...
Give it some more effort! Math takes a lot of time.